Data Driven Smooth Test Against Stochastic Dominance

Performs data driven smooth non-parametric two-sample test against one-sided alternatives (stochastic dominance). Suppose that we have random samples from two distributions F and G. The null hypothesis is that F(x) < G(x) for some x while the alternative is that at F(x) >= G(x) for all x with strict inequality for at least one x. Detailed description of the test statistic is provided in Ledwina and Wylupek (2012).

ddst.againststochdom.test(
  x,
  y,
  k.N = 4,
  alpha = 0.05,
  t,
  nr = 1e+05,
  compute.cv = FALSE
)

Arguments

x	a (non-empty) numeric vector of data
y	a (non-empty) numeric vector of data
k.N	an integer specifying a level of complexity of the grid considered, only for advanced users
alpha	a significance level
t	an alpha-dependent tunning parameter in the penalty in the model selection rule
nr	an integer specifying the number of runs for a p-value and a critical value computation if any
compute.cv	a logical value indicating whether to compute a critical value corresponding to the significance level alpha or not

References

Two-sample test against one-sided alternatives. Ledwina and Wylupek (2012). https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-9469.2011.00787.x

Examples

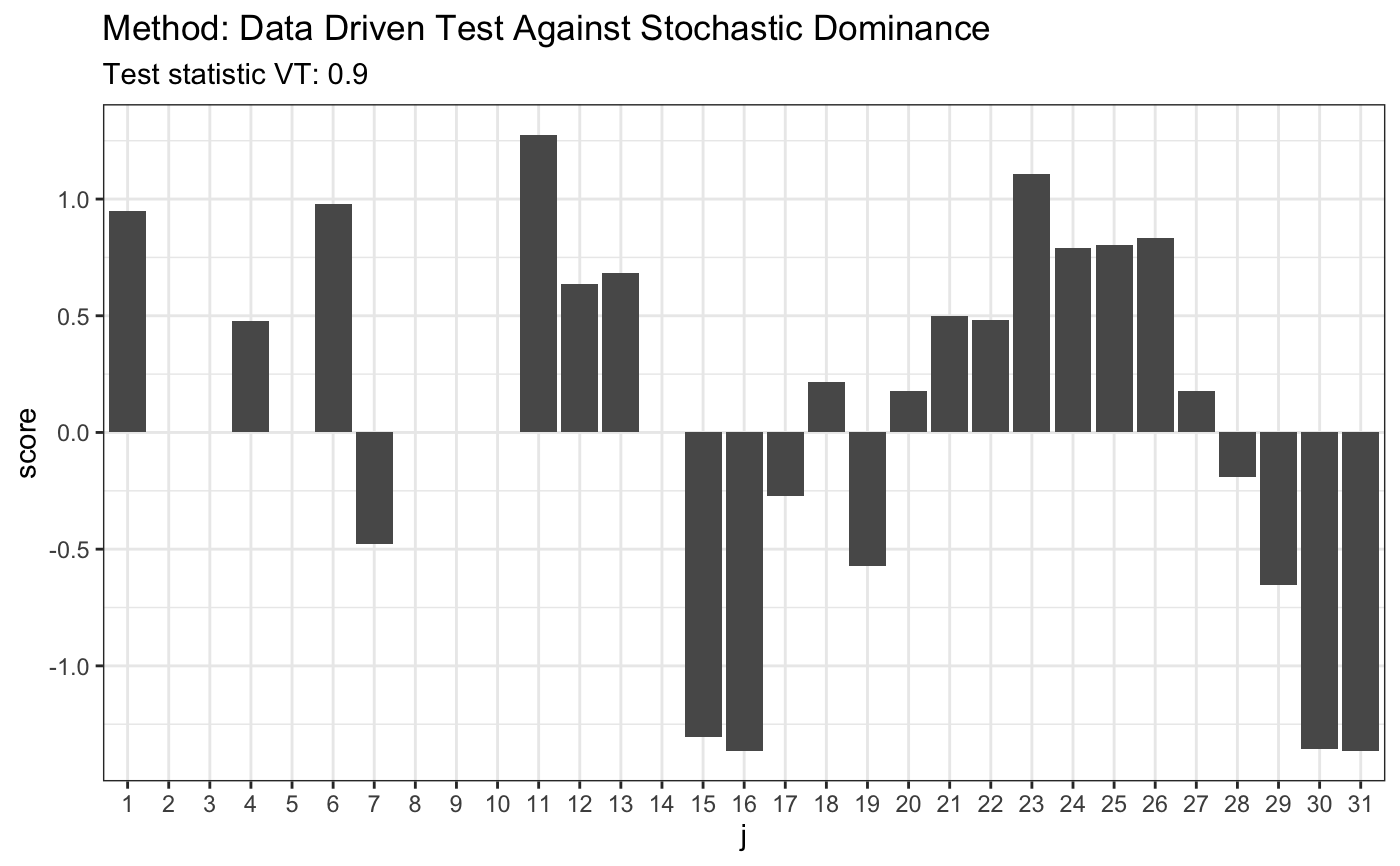
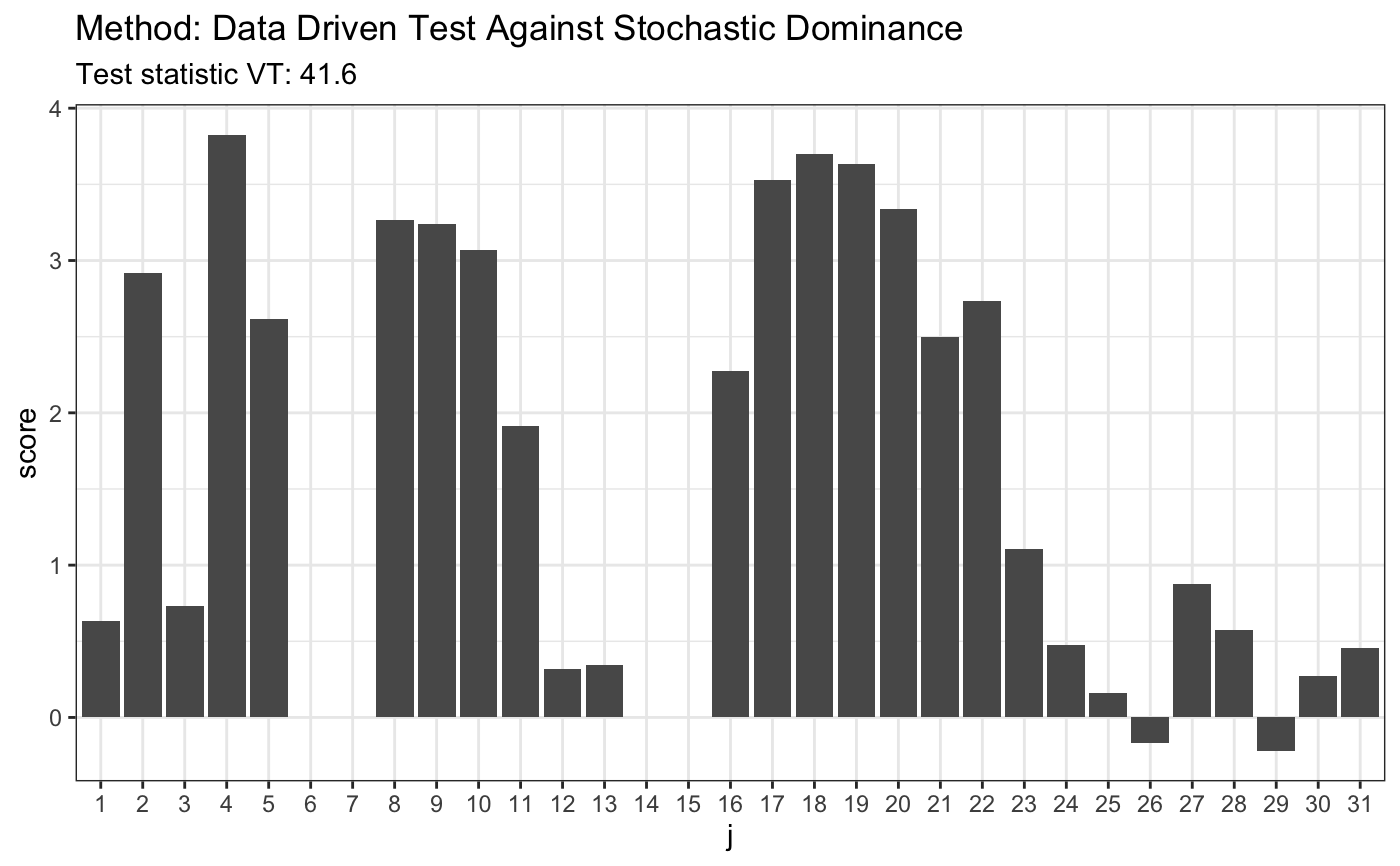
set.seed(7)
# H0 is true
x <- runif(80)
y <- runif(80)
t <- ddst.againststochdom.test(x, y, alpha = 0.05, t = 2.2, k.N = 4)
t
#> 
#> 	Data Driven Test Against Stochastic Dominance
#> 
#> data:  x, alpha: 0.05, t: 2.2, k.N: 4
#> VT = 0.9, T = 1
#> 
plot(t)

# H0 is false
# known fixed alternative
x <- runif(80)
y <- rbeta(80,4,2)
t <- ddst.againststochdom.test(x, y, alpha = 0.05, t = 2.2, k.N = 4)
t
#> 
#> 	Data Driven Test Against Stochastic Dominance
#> 
#> data:  x, alpha: 0.05, t: 2.2, k.N: 4
#> VT = 41.6, T = 5
#> 
plot(t)