Data Driven Smooth Test for Extreme Value Distribution

Performs data driven smooth test for composite hypothesis of extreme value distribution. Null density is given by \( f(z;\gamma)=1/\gamma_2 \exp((z-\gamma_1)/\gamma_2- \exp((z-\gamma_1)/\gamma_2))\), \(z \in R\).

ddst.evd.test(
  x,
  base = ddst.base.legendre,
  d.n = 10,
  c = 100,
  nr = 1e+05,
  compute.p = TRUE,
  alpha = 0.05,
  compute.cv = TRUE,
  ...
)

Arguments

x	a (non-empty) numeric vector of data values
base	a function which returns an orthonormal system, possible choice: ddst.base.legendre for the Legendre polynomials and ddst.base.cos for the cosine system
d.n	an integer specifying the maximum dimension considered, only for advanced users
c	a calibrating parameter in the penalty in the model selection rule
nr	an integer specifying the number of runs for a p-value and a critical value computation if any
compute.p	a logical value indicating whether to compute a p-value or not
alpha	a significance level
compute.cv	a logical value indicating whether to compute a critical value corresponding to the significance level alpha or not
...	further arguments

Value

An object of class htest

statistic

the value of the test statistic.

parameter

the number of choosen coordinates (k).

method

a character string indicating the parameters of performed test.

data.name

a character string giving the name(s) of the data.

p.value

the p-value for the test, computed only if compute.p=TRUE.

Details

We model alternatives similarly as in Kallenberg and Ledwina (1997) and Janic-Wroblewska (2004) using Legendre's polynomials or cosines. For more details see: http://www.biecek.pl/R/ddst/description.pdf.

References

Hosking, J.R.M., Wallis, J.R., Wood, E.F. (1985). Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. \( Technometrics\) 27, 251--261.

Janic-Wroblewska, A. (2004). Data-driven smooth test for extreme value distribution. \( Statistics\) 38, 413--426.

Janic, A. and Ledwina, T. (2008). Data-driven tests for a location-scale family revisited. \( J. Statist. Theory. Pract. Special issue on Modern Goodness of Fit Methods. accepted.\).

Kallenberg, W.C.M., Ledwina, T. (1997). Data driven smooth tests for composite hypotheses: Comparison of powers. \( J. Statist. Comput. Simul.\) 59, 101--121.

Examples

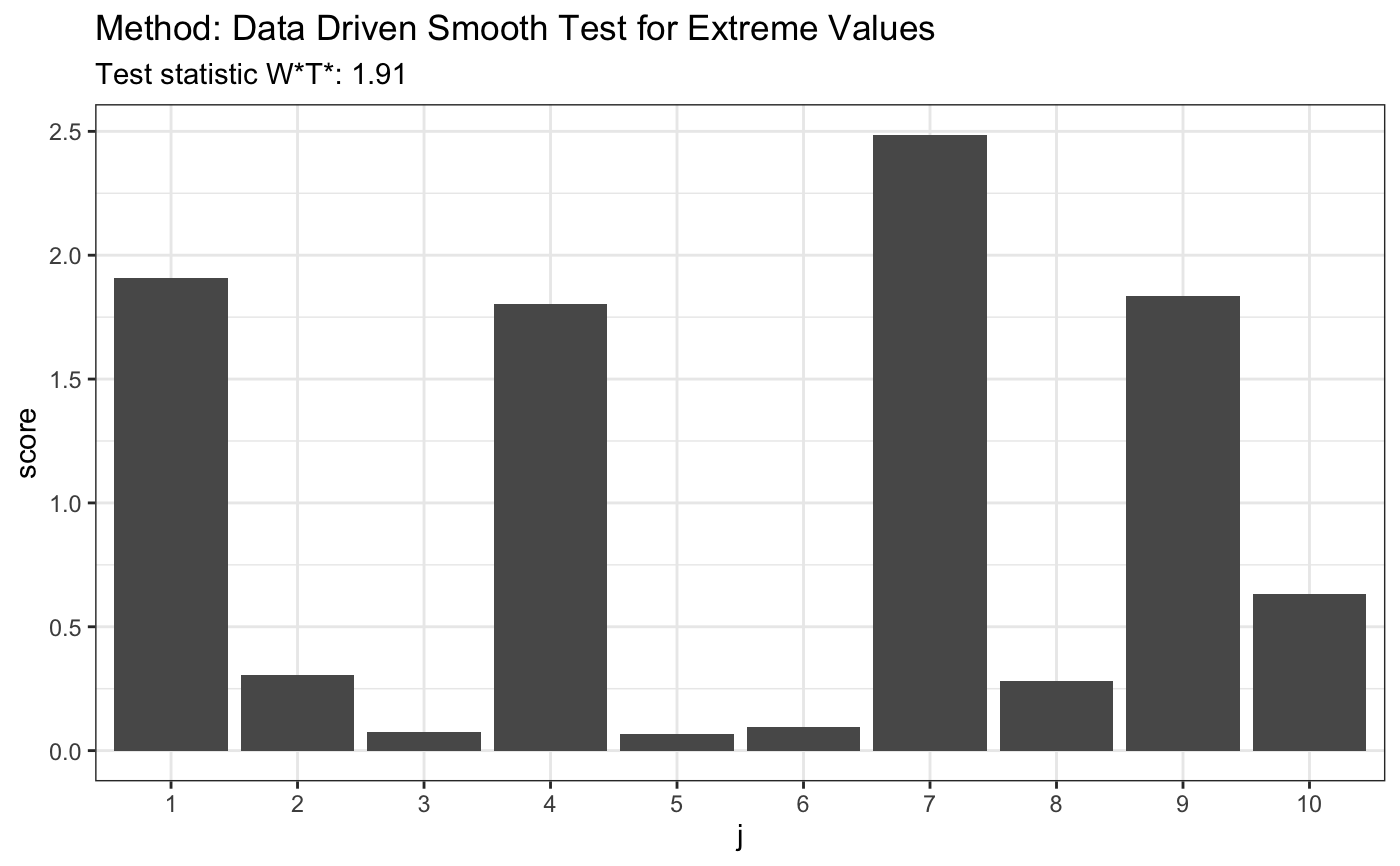
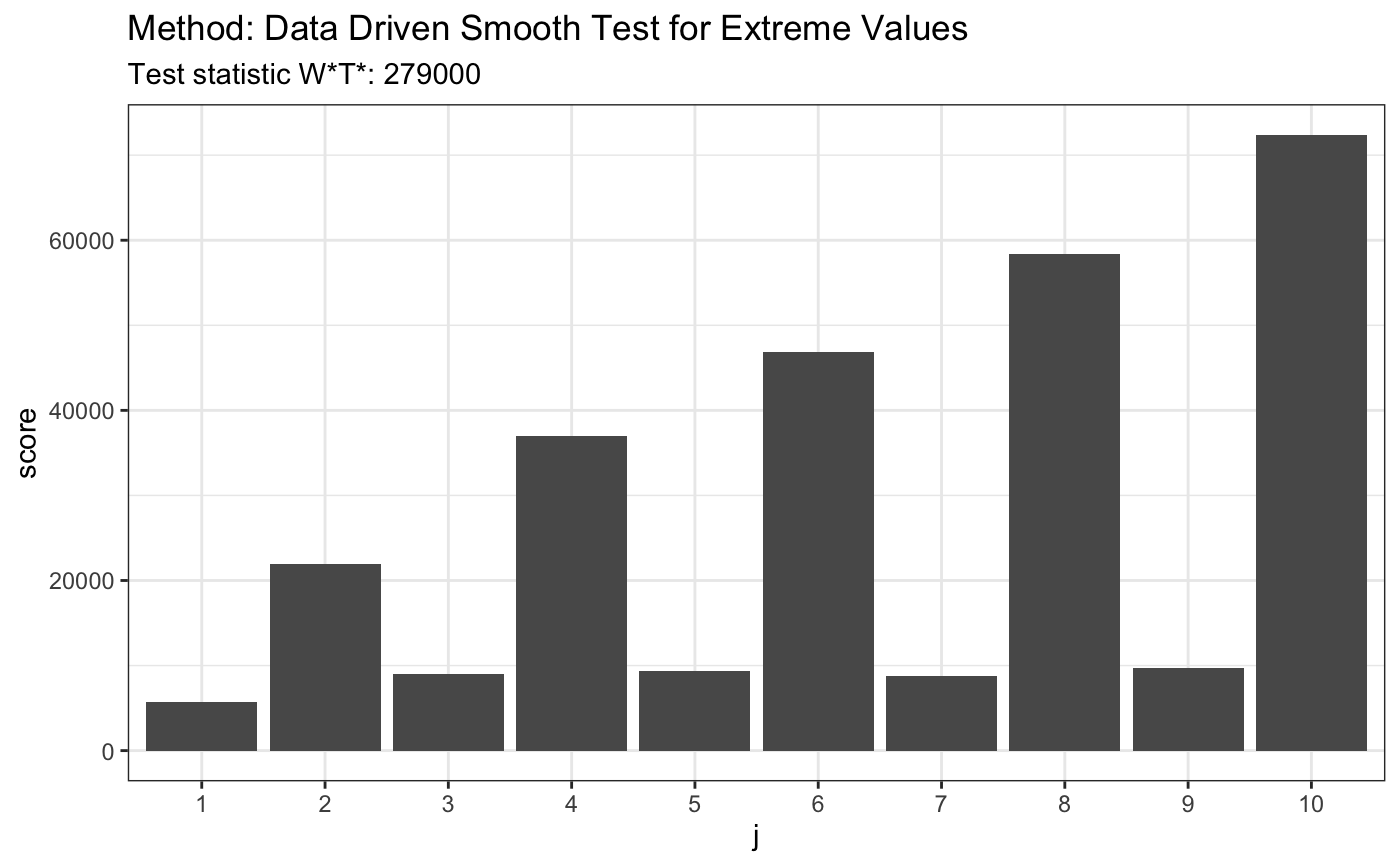
library(evd)
set.seed(7)

# for given vector of 19 numbers
z <- c(13.41, 6.04, 1.26, 3.67, -4.54, 2.92, 0.44, 12.93, 6.77, 10.09,
      4.10, 4.04, -1.97, 2.17, -5.38, -7.30, 4.75, 5.63, 8.84)
t <- ddst.evd.test(z, compute.p = TRUE, d.n = 10)
t
#> 
#> 	Data Driven Smooth Test for Extreme Values
#> 
#> data:  z, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 1.9073, T* = 1, p-value = 0.5904
#> 
plot(t)

# H0 is true
x <- -qgumbel(runif(100),-1,1)
t <- ddst.evd.test (x, compute.p = TRUE, d.n = 10)
t
#> 
#> 	Data Driven Smooth Test for Extreme Values
#> 
#> data:  x, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 0.032805, T* = 1, p-value = 0.9999
#> 
plot(t)

# H0 is false
x <- rexp(80,4)
t <- ddst.evd.test (x, compute.p = TRUE, d.n = 10)
t
#> 
#> 	Data Driven Smooth Test for Extreme Values
#> 
#> data:  x, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 279210, T* = 10, p-value = 1e-04
#> 
plot(t)