Data Driven Smooth Test for Normality; Bounded Basis Functions

Performs data driven smooth test for composite hypothesis of normality Null density is given by \( f(z;\gamma)=1/(\sqrt{2 \pi}\gamma_2) \exp(-(z-\gamma_1)^2/(2 \gamma_2^2))\) for \(z \in R\). We model alternatives similarly as in Kallenberg and Ledwina (1997 a,b) using Legendre's polynomials or cosine basis.

ddst.normbounded.test(
  x,
  base = ddst.base.legendre,
  d.n = 10,
  c = 100,
  compute.p = TRUE,
  alpha = 0.05,
  compute.cv = TRUE,
  ...
)

Arguments

x	a (non-empty) numeric vector of data values
base	a function which returns an orthonormal system, possible choice: ddst.base.legendre for the Legendre polynomials and ddst.base.cos for the cosine system
d.n	an integer specifying the maximum dimension considered, only for advanced users
c	a calibrating parameter in the penalty in the model selection rule
compute.p	a logical value indicating whether to compute a p-value or not
alpha	a significance level
compute.cv	a logical value indicating whether to compute a critical value corresponding to the significance level alpha or not
...	further arguments

Value

An object of class htest

statistic

the value of the test statistic.

parameter

the number of choosen coordinates (k).

method

a character string indicating the parameters of performed test.

data.name

a character string giving the name(s) of the data.

p.value

the p-value for the test, computed only if compute.p = TRUE.

References

Chen, L., Shapiro, S.S. (1995). An alternative test for normality based on normalized spacings. J. Statist. Comput. Simulation 53, 269--288.

Inglot, T., Ledwina, T. (2006). Towards data driven selection of a penalty function for data driven Neyman tests. Linear Algebra and its Appl. 417, 579--590.

Janic, A. and Ledwina, T. (2008). Data-driven tests for a location-scale family revisited. J. Statist. Theory. Pract. Special issue on Modern Goodness of Fit Methods..

Kallenberg, W.C.M., Ledwina, T. (1997 a). Data driven smooth tests for composite hypotheses: Comparison of powers. J. Statist. Comput. Simul. 59, 101--121.

Kallenberg, W.C.M., Ledwina, T. (1997 b). Data driven smooth tests when the hypothesis is composite. J. Amer. Statist. Assoc. 92, 1094--1104.

Examples

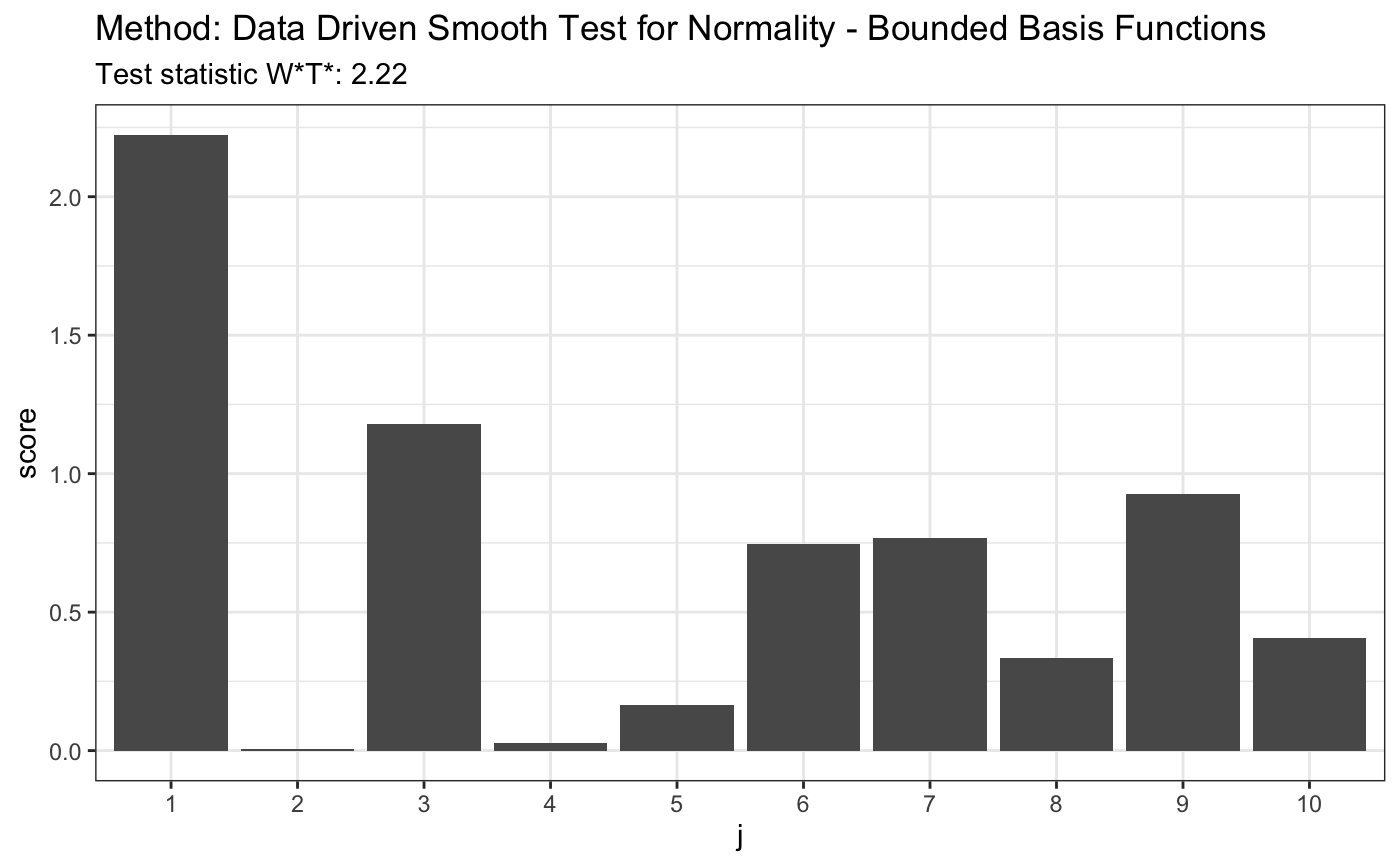
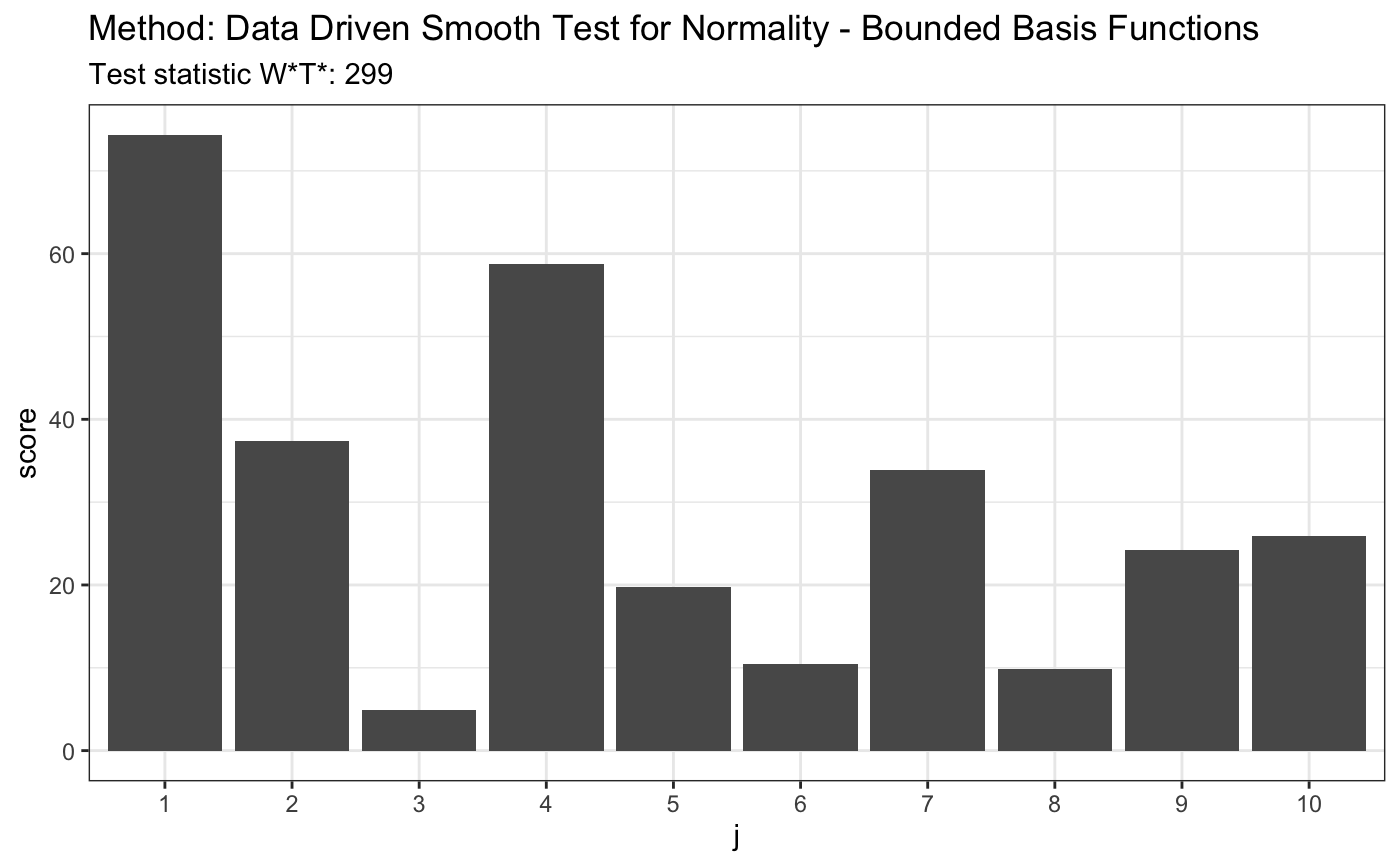
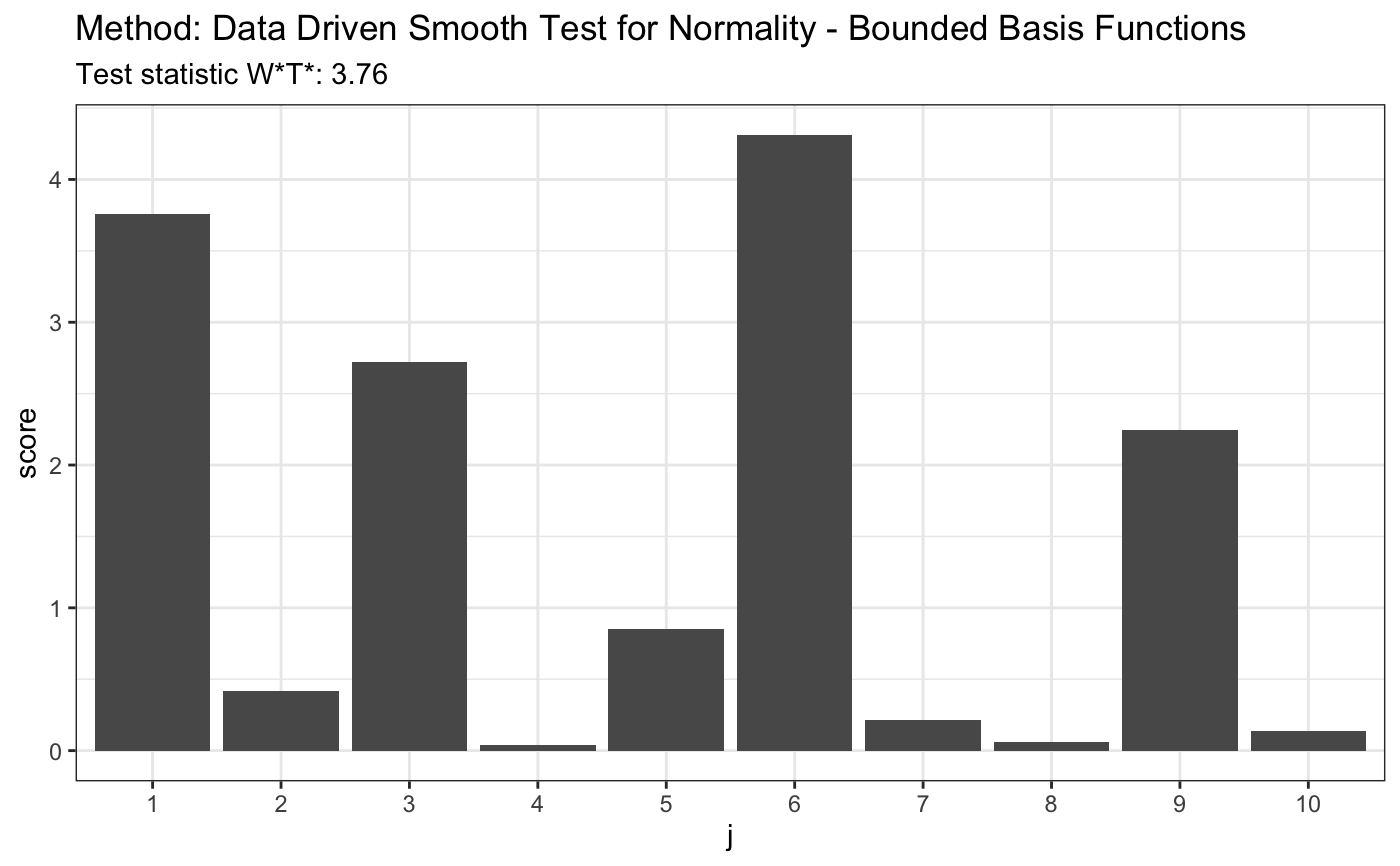
set.seed(7)
# H0 is true
z <- rnorm(100)
# let's look on first 10 coordinates
d.n <- 10
t <- ddst.normbounded.test(z, compute.p = TRUE, d.n = d.n)
t
#> 
#> 	Data Driven Smooth Test for Normality - Bounded Basis Functions
#> 
#> data:  z, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 2.2232, T* = 1, p-value = 0.1581
#> 
plot(t)

# H0 is false
z <- rexp(100, 1)
t <- ddst.normbounded.test(z, compute.p = TRUE, d.n = d.n)
t
#> 
#> 	Data Driven Smooth Test for Normality - Bounded Basis Functions
#> 
#> data:  z, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 299.45, T* = 10, p-value < 2.2e-16
#> 
plot(t)

# for Tephra data
z <- c(-1.748789, -1.75753, -1.740102, -1.740102, -1.731467, -1.765523,
      -1.761521, -1.72522, -1.80371, -1.745624, -1.872957, -1.729121,
      -1.81529, -1.888637, -1.887761, -1.881645, -1.91518, -1.849769,
      -1.755141, -1.665687, -1.764721, -1.736171, -1.736956, -1.737742,
      -1.687537, -1.804534, -1.790593, -1.808661, -1.784081, -1.729903,
      -1.711263, -1.748789, -1.772755, -1.72756, -1.71358, -1.821116,
      -1.839588, -1.839588, -1.830321, -1.807835, -1.747206, -1.788147,
      -1.759923, -1.786519, -1.726779, -1.738528, -1.754345, -1.781646,
      -1.641949, -1.755936, -1.775175, -1.736956, -1.705103, -1.743255,
      -1.82613, -1.826967, -1.780025, -1.684504, -1.751168)
t <- ddst.normbounded.test(z, compute.p = TRUE, d.n = d.n)
t
#> 
#> 	Data Driven Smooth Test for Normality - Bounded Basis Functions
#> 
#> data:  z, base: ddst.base.legendre, c: 100, d.n: 10
#> W*T* = 3.7615, T* = 1, p-value = 0.08891
#> 
plot(t)