Data Driven Smooth Test for Uniformity

Performs data driven smooth tests for simple hypothesis of uniformity on [0,1]. Embeding null model into the original exponential family introduced by Neyman (1937).

ddst.uniform.test(
  x,
  base = ddst.base.legendre,
  d.n = 10,
  c = 2.4,
  nr = 1e+05,
  compute.p = TRUE,
  alpha = 0.05,
  compute.cv = TRUE,
  ...
)

Arguments

x	a (non-empty) numeric vector of data
base	a function which returns an orthonormal system, possible choice: ddst.base.legendre for the Legendre polynomials and ddst.base.cos for the cosine system
d.n	an integer specifying the maximum dimension considered, only for advanced users
c	a calibrating parameter in the penalty in the model selection rule
nr	an integer specifying the number of runs for a p-value and a critical value computation if any
compute.p	a logical value indicating whether to compute a p-value or not
alpha	a significance level
compute.cv	a logical value indicating whether to compute a critical value corresponding to the significance level alpha or not
...	further arguments

Value

An object of class htest

statistic

the value of the test statistic.

parameter

the number of choosen coordinates (k).

method

a character string indicating the parameters of performed test.

data.name

a character string giving the name(s) of the data.

p.value

the p-value for the test, computed only if compute.p=T.

References

Inglot, T., Ledwina, T. (2006). Towards data driven selection of a penalty function for data driven Neyman tests. Linear Algebra and its Appl. 417, 579--590.

Ledwina, T. (1994). Data driven version of Neyman's smooth test of fit. J. Amer. Statist. Assoc. 89 1000-1005.

Neyman, J. (1937). `Smooth test' for goodness of fit. Skand. Aktuarietidskr. 20, 149-199.

Examples

set.seed(7)
# H0 is true
z <- runif(80)
t <- ddst.uniform.test(z, compute.p = TRUE, d.n = 10)
t
#> 
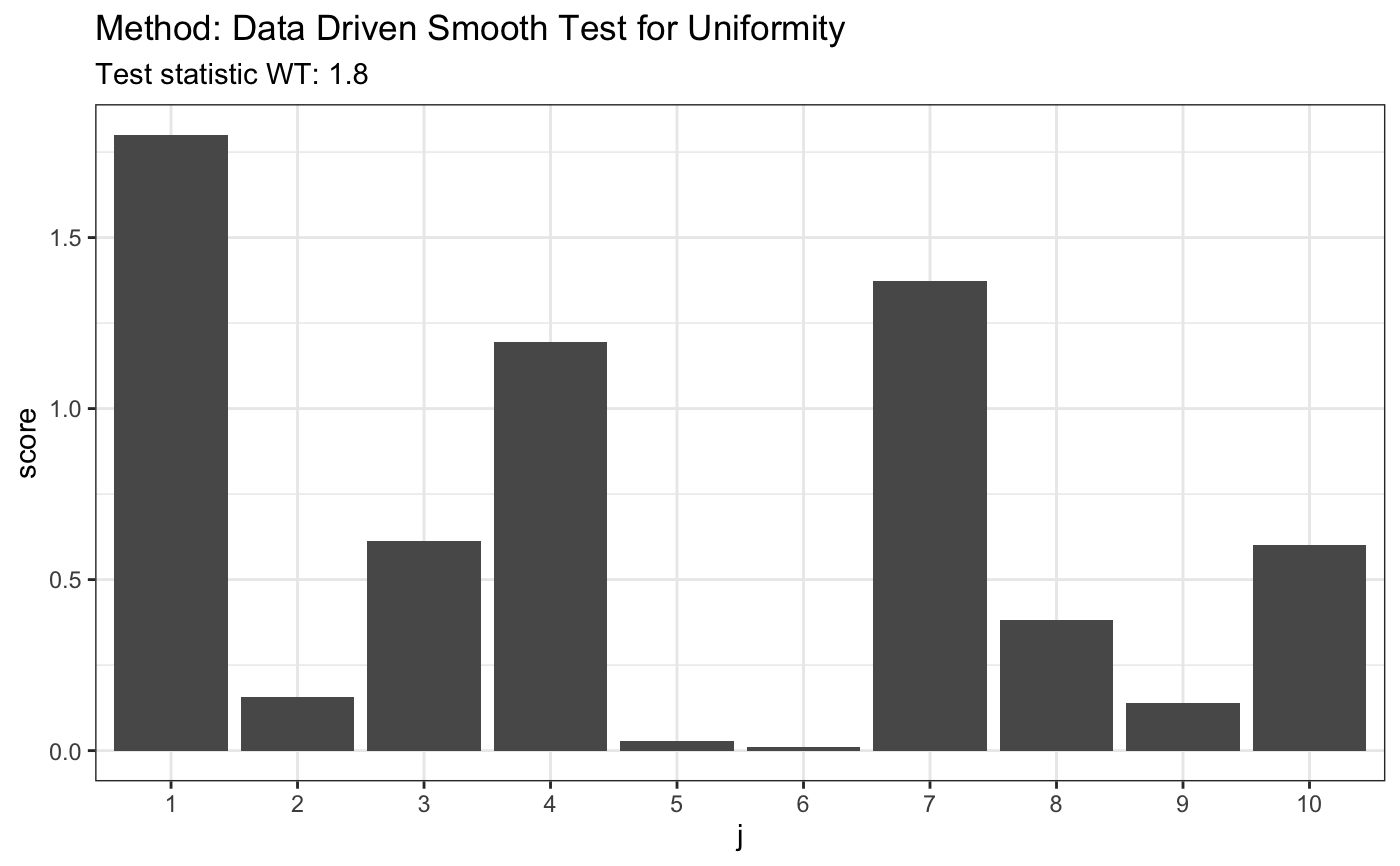
#> 	Data Driven Smooth Test for Uniformity
#> 
#> data:  z, base: ddst.base.legendre  c: 2.4  d.n: 10  cv(0.05) : 0.0045668)
#> WT = 0.31054, T = 1, p-value = 0.5989
#> 
plot(t)

# known fixed alternative
z <- rnorm(80,10,16)
t <- ddst.uniform.test(pnorm(z, 10, 16), compute.p = TRUE, d.n = 10)
t
#> 
#> 	Data Driven Smooth Test for Uniformity
#> 
#> data:  pnormz1016, base: ddst.base.legendre  c: 2.4  d.n: 10  cv(0.05) : 0.0041374)
#> WT = 1.8002, T = 1, p-value = 0.2205
#> 
plot(t)

# H0 is false
z <- rbeta(80,4,2)
(t <- ddst.uniform.test(z, compute.p = TRUE, d.n = 10))
#> 
#> 	Data Driven Smooth Test for Uniformity
#> 
#> data:  z, base: ddst.base.legendre  c: 2.4  d.n: 10  cv(0.05) : 0.0043749)
#> WT = 57.602, T = 4, p-value < 2.2e-16
#> 
t$p.value
#> [1] 0
plot(t)