1 Introduction
1.1 The aim of the book
Predictive models are used to guess (statisticians would say: predict) values of a variable of interest based on values of other variables. As an example, consider prediction of sales based on historical data, prediction of the risk of heart disease based on patient’s characteristics, or prediction of political attitudes based on Facebook comments.
Predictive models have been used throughout the entire human history. Ancient Egyptians, for instance, used observations of the rising of Sirius to predict the flooding of the Nile. A more rigorous approach to model construction may be attributed to the method of least squares, published more than two centuries ago by Legendre in 1805 and by Gauss in 1809. With time, the number of applications in the economics, medicine, biology, and agriculture has grown. The term regression was coined by Francis Galton in 1886. Initially, it referred to biological applications, while today it is used for various models that allow prediction of continuous variables. Prediction of nominal variables is called classification, and its beginning may be attributed to works of Ronald Fisher in 1936.
During the last century, many statistical models that can be used for predictive purposes have been developed. These include linear models, generalized linear models, classification and regression trees, rule-based models, and many others. Developments in mathematical foundations of predictive models were boosted by increasing computational power of personal computers and availability of large datasets in the era of “big data” that we have entered.
With the increasing demand for predictive models, model properties such as flexibility, capability of internal variable selection or feature engineering, and high precision of predictions are of interest. To obtain robust models, ensembles of models are used. Techniques like bagging, boosting, or model stacking combine hundreds or thousands of simpler models into one super-model. Large deep-neural models may have over a billion parameters.
There is a cost of this progress. Complex models may seem to operate like “black boxes”. It may be difficult, or even impossible, to understand how thousands of variables affect a model’s prediction. At the same time, complex models may not work as well as we would like them to. An overview of real problems with massive-scale black-box models may be found in an excellent book by O’Neil (2016) or in her TED Talk “The era of blind faith in big data must end”. There is a growing number of examples of predictive models with performance that deteriorated over time or became biased in some sense. For instance, IBM’s Watson for Oncology was criticized by oncologists for delivering unsafe and inaccurate recommendations (Ross and Swetliz 2018). Amazon’s system for curriculum-vitae screening was found to be biased against women (Dastin 2018). The COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) algorithm for predicting recidivism, developed by Northpointe (now Equivant), was accused of bias against African-Americans (Larson et al. 2016). Algorithms behind the Apple Credit Card are accused of being gender-biased (Duffy 2019). Some tools for sentiment analysis are suspected of age-bias (Diaz et al. 2018). These are examples of models and algorithms that led to serious violations of fairness and ethical principles. An example of a situation when data-drift led to a deterioration in model performance is the Google Flu model, which gave worse predictions after two years than at baseline (Salzberg 2014; Lazer et al. 2014).
A reaction to some of these examples and issues are new regulations, like the General Data Protection Regulation (GDPR 2018). Also, new civic rights are being formulated (Goodman and Flaxman 2017; Casey, Farhangi, and Vogl 2019; Ruiz 2018). A noteworthy example is the “Right to Explanation”, i.e., the right to be provided with an explanation for an output of an automated algorithm (Goodman and Flaxman 2017). To exercise the right, we need new methods for verification, exploration, and explanation of predictive models.
Figure 1.1 presents an attempt to summarize how the increase in the model complexity affects the relative importance of domain understanding, the choice of a model, and model validation.
In classical statistics, models are often built as a result of a good understanding of the application domain. Domain knowledge helps to create and select the most important variables that can be included in relatively simple models that yield predictive scores. Model validation is based mainly on the evaluation of the goodness-of-fit and hypothesis testing. Statistical hypotheses shall be stated before data analysis, and obtained p-values should not interfere with the way in which data were processed or models were constructed.
Machine learning, on the other hand, exploits the trade-off between the availability of data and domain knowledge. The effort is shifted from a deep understanding of the application domain towards (computationally heavy) construction and fitting of models. Flexible models can use massive amounts of data to select informative variables and filter out uninformative ones. The validation step gains in importance because it provides feedback to the model construction.
How might this approach look in the future? It is possible that the increasing automation of the exploratory data analysis (EDA) and the modelling part of the process will shift the focus towards the validation of a model. In particular, validation will not only focus on how good a model’s fit and predictions are but also what other risks (like concept drift) or biases may be associated with the model. Model exploration will allow us to better and faster understand the analyzed data.
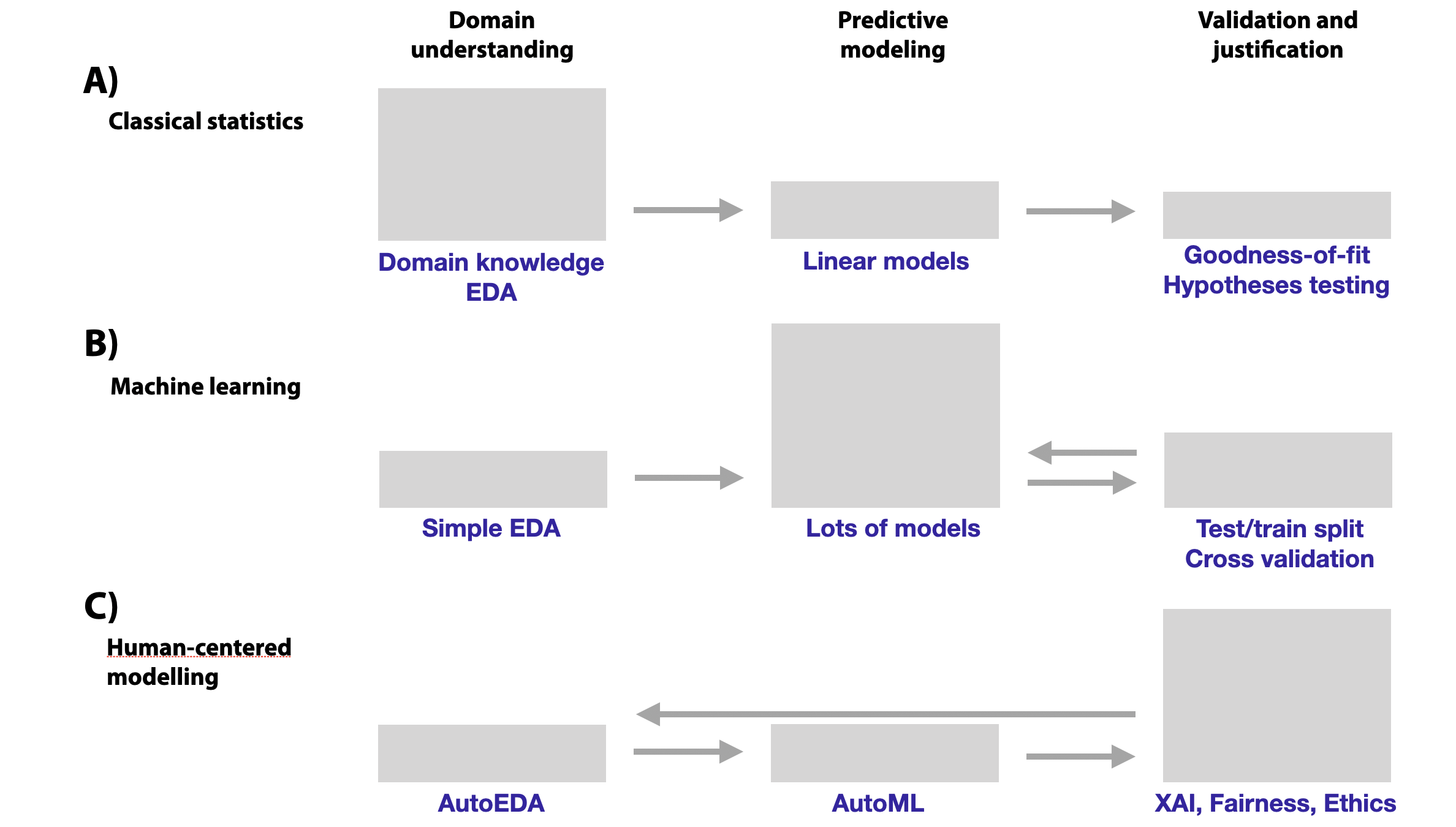
Figure 1.1: Shift in the relative importance and effort (symbolically represented by the shaded boxes) put in different phases of data-driven modelling. Arrows show feedback loops in the modelling process. (A) In classical statistics, modelling is often based on a deep understanding of the application domain combined with exploratory data analysis (EDA). Most often, (generalized) linear models are used. Model validation includes goodness-of-fit evaluation and hypothesis testing. (B) In machine learning (ML), domain knowledge and EDA are often limited. Instead, flexible models are fitted to large volumes of data to obtain a model offering a good predictive performance. Evaluation of the performance (applying strategies like cross-validation to deal with overfitting) gains in importance, as validation provides feedback to model construction. (C) In the (near?) future, auto-EDA and auto-ML will shift focus even further to model validation that will include the use of explainable artificial intelligence (XAI) techniques and evaluation of fairness, ethics, etc. The feedback loop is even longer now, as the results from model validation will also be helping in domain understanding.
Summarizing, we can conclude that, today, the true bottleneck in predictive modelling is neither the lack of data, nor the lack of computational power, nor inadequate algorithms, nor the lack of flexible models. It is the lack of tools for model exploration and, in particular, model explanation (obtaining insight into model-based predictions) and model examination (evaluation of model’s performance and understanding the weaknesses). Thus, in this book, we present a collection of methods that may be used for this purpose. As development of such methods is a very active area of research, with new methods becoming available almost on a continuous basis, we do not aim at being exhaustive. Rather, we present the mindset, key concepts and issues, and several examples of methods that can be used in model exploration.
1.2 A bit of philosophy: three laws of model explanation
In 1942, in his story “Runaround”, Isaac Asimov formulated Three Laws of Robotics:
- a robot may not injure a human being,
- a robot must obey the orders given it by human beings, and
- a robot must protect its own existence.
Today’s robots, like cleaning robots, robotic pets, or autonomous cars are far from being conscious enough to fall under Asimov’s ethics. However, we are more and more surrounded by complex predictive models and algorithms used for decision-making. Artificial-intelligence models are used in health care, politics, education, justice, and many other areas. The models and algorithms have a far larger influence on our lives than physical robots. Yet, applications of such models are left unregulated despite examples of their potential harmfulness. An excellent overview of selected issues is offered in the book by O’Neil (2016).
It is now becoming clear that we have got to control the models and algorithms that may affect us. Asimov’s laws are being referred to in the context of the discussion around ethics of artificial intelligence (https://en.wikipedia.org/wiki/Ethics_of_artificial_intelligence). Initiatives to formulate principles for artificial-intelligence development have been undertaken, for instance, in the UK (Olhede and Wolfe 2018). Following Asimov’s approach, we propose three requirements that any predictive model should fulfil:
- Prediction’s validation. For every prediction of a model, one should be able to verify how strong the evidence is that supports the prediction.
- Prediction’s justification. For every prediction of a model, one should be able to understand which variables affect the prediction and to what extent.
- Prediction’s speculation. For every prediction of a model, one should be able to understand how the prediction would change if the values of the variables included in the model changed.
We see two ways to comply with these requirements. One is to use only models that fulfil these conditions by design. These are so-called “interpretable-by-design models” that include linear models, rule-based models, or classification trees with a small number of parameters (Molnar 2019). However, the price of transparency may be a reduction in performance. Another way is to use tools that allow, perhaps by using approximations or simplifications, “explaining” predictions for any model. In our book, we focus on the latter approach.
1.3 Terminology
It is worth noting that, when it comes to predictive models, the same concepts have often been given different names in statistics and in machine learning. In his famous article (Leo Breiman 2001b), Leo Breiman described similarities and differences in perspectives used by the two communities. For instance, in the statistical-modelling literature, one refers to “explanatory variables”, with “independent variables”, “predictors”, or “covariates” often used as equivalents. Explanatory variables are used in a model as a means to explain (predict) the “dependent variable”, also called “predicted” variable or “response”. In machine-learning terminology, “input variables” or “features” are used to predict the “output” or “target” variable. In statistical modelling, models are “fit” to the data that contain “observations”, whereas in the machine-learning world a model is “trained” on a dataset that may contain “instances” or “cases”. When we talk about numerical constants that define a particular version of a model, in statistical modelling, we refer to model “coefficients”, while in machine learning it is more customary to refer to model “parameters”. In statistics, it is common to say that model coefficients are “estimated”, while in machine learning it is more common to say that parameters are “trained”.
To the extent possible, in our book we try to consistently use the statistical-modelling terminology. However, the reader may find references to a “feature” here and there. Somewhat inconsistently, we also introduce the term “instance-level” explanation. Instance-level explanation methods are designed to extract information about the behaviour of a model related to a specific observation (or instance). On the other hand, “dataset-level” explanation techniques allow obtaining information about the behaviour of the model for an entire dataset.
We consider models for dependent variables that can be continuous or categorical. The values of a continuous variable can be represented by numbers with an ordering that makes some sense (ZIP-codes or phone numbers are not considered as continuous variables, while age or number of children are). A continuous variable does not have to be continuous in the mathematical sense; counts (number of floors, steps, etc.) will be treated as continuous variables as well. A categorical variable can assume only a finite set of values that are not numbers in the mathematical sense, i.e., it makes no sense to subtract or divide these values.
In this book, we treat models as “black boxes”. We don’t assume anything about their internal structure or complexity. We discuss the specificity of such an approach in a bit more detail in the next section.
1.4 Black-box models and glass-box models
Usually, the term “black-box” model is used for models with a complex structure that is hard to understand by humans. This usually refers to a large number of model coefficients or complex mathematical transformations. As people vary in their capacity to understand complex models, there is no strict threshold for the number of coefficients that makes a model a black box. In practice, for most people, this threshold is probably closer to 10 than to 100.
A “glass-box” (sometimes also called a “white-box” or a “transparent-box”) model, which is opposite to a black-box one, is a model that is easy to understand (though maybe not by every person). It has a simple structure and a limited number of coefficients.
The most common classes of glass-box models are decision or regression trees (see an example in Figure 1.2), or models with an explicit compact structure. As an example of the latter, consider a model for obesity based on the body-mass index (BMI), with BMI defined as the mass (in kilograms) divided by the square of height (in meters). Subjects are classified as underweight if their BMI<18, as normal if their BMI lies in the interval [18,25], and as overweight if their BMI>25. The compact form of the model makes it easy to understand, for example, how does a change in BMI change the predicted obesity class.
The structure of a glass-box model is, in general, easy to understand. It may be difficult to collect the necessary data, build the model, fit it to the data, or perform model validation, but once the model has been developed its interpretation and mode of working is straightforward.
Why is it important to understand a model’s structure? There are several important advantages. If the structure is transparent, we can easily see which explanatory variables are included in the model and which are not. Hence, for instance, we may be able to question the model from which a particular explanatory variable is excluded. Also, in the case of a model with a transparent structure and a limited number of coefficients, we can easily link changes in the model’s predictions with changes in particular explanatory variables. This, in turn, may allow us to challenge the model on the ground of domain knowledge if, for instance, the effect of a particular variable on predictions is inconsistent with previously-established results. Note that linking changes in the model’s predictions to changes in particular explanatory variables may be difficult when there are many variables and/or coefficients in the model. For instance, a classification tree with hundreds of nodes is difficult to understand, as is a linear regression model with hundreds of coefficients.
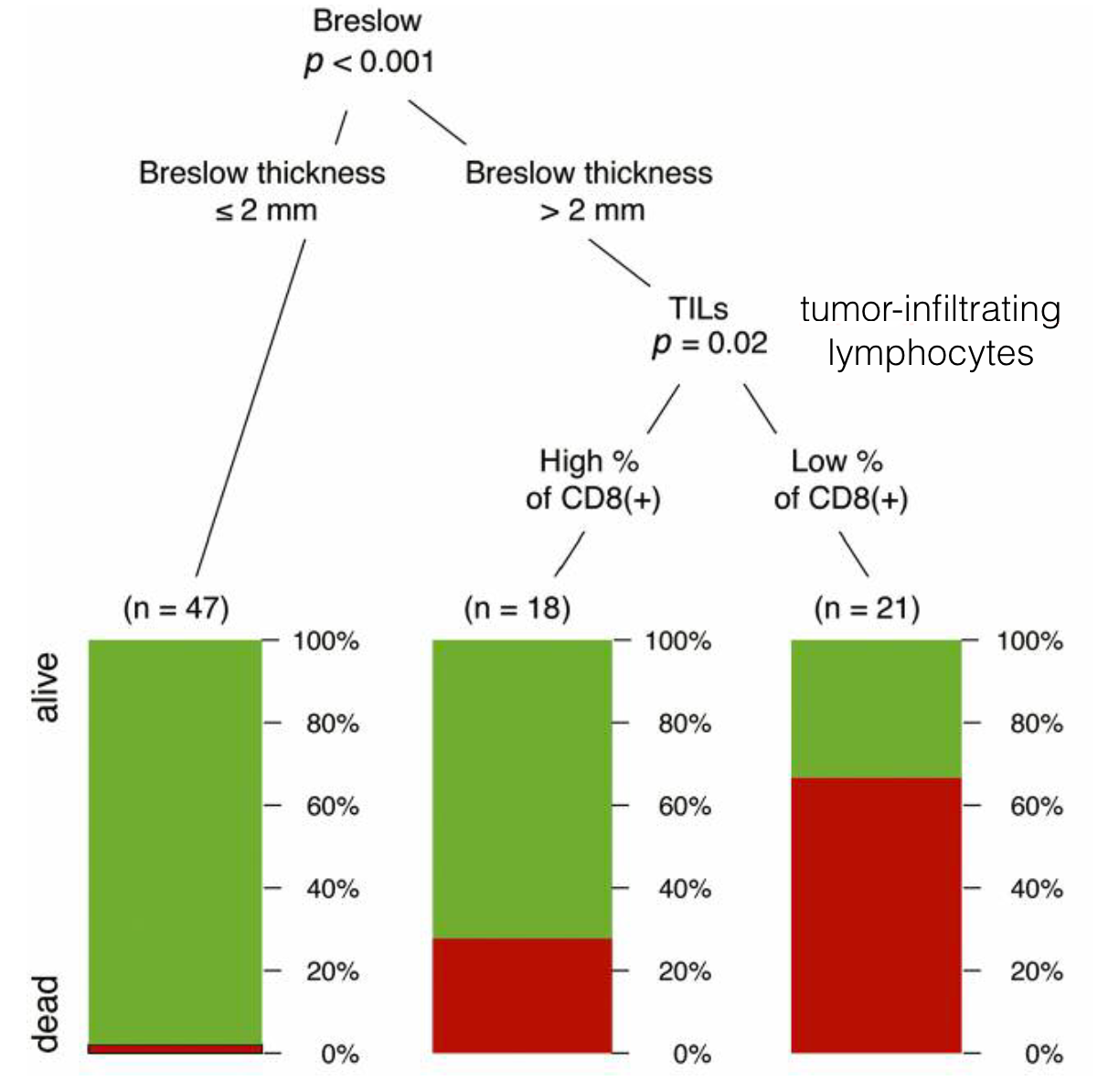
Figure 1.2: An example of a decision-tree model for melanoma risk patients developed by Donizy et al. (2016). The model is based on two explanatory variables, Breslow thickness and the presence of tumor infiltration lymphocytes. These two variables classify patients into three groups with a different probability of survival.
Note that some glass-box models, like the decision-tree model presented in Figure 1.2, satisfy by design the explainability laws introduced in Section 1.2. In particular, regarding prediction’s validation, we see how many patients fall in a given category in each node. With respect to prediction’s justification, we know which explanatory variables are used in every decision path. Finally, regarding prediction’s speculation, we can trace how changes in particular variables will affect the model’s prediction. We can, of course, argue if the model is good or not, but the model structure is obviously transparent.
Comprehending the performance of black-box models presents more challenges. The structure of a complex model, such as, for example, a neural-network model, may be far from transparent. Consequently, we may not understand which features influence the model decisions and by how much. Consequently, it may be difficult to decide whether the model is consistent with our domain knowledge.
In our book, we present tools that can help in extracting the information necessary for the evaluation of models in a model-agnostic fashion, i.e., in the same way regardless of the complexity of the analyzed model.
1.5 Model-agnostic and model-specific approach
Interest in model interpretability is as old as statistical modelling itself. Some classes of models have been developed for a long period or have attracted intensive research. Consequently, those classes of models are equipped with excellent tools for model exploration, validation, or visualisation. For example:
- There are many tools for diagnostics and evaluation of linear models (see, for example, Galecki and Burzykowski (2013) or Faraway (2005)). Model assumptions are formally defined (normality, linear structure, homogeneity of variance) and can be checked by using normality tests or plots (like normal qq-plots), diagnostic plots, tests for model structure, tools for identification of outliers, etc. A similar situation applies to generalized linear models (see, for example, Dobson (2002)).
- For more advanced models with an additive structure, like the proportional hazards model, many tools can be used for checking model assumptions (see, for example, Harrell Jr (2018) or Sheather (2009)).
- Random forest models are equipped with the out-of-bag method of evaluating performance and several tools for measuring variable importance (Breiman et al. 2018). Methods have been developed to extract information about possible interactions from the model structure (Paluszynska and Biecek 2017; Ehrlinger 2016). Similar tools have been developed for other ensembles of trees, like boosting models (see, for example, Foster (2017) or Karbowiak and Biecek (2019)).
- Neural networks enjoy a large collection of dedicated model-explanation tools that use, for instance, the layer-wise relevance propagation technique (Bach et al. 2015), saliency maps technique (Simonyan, Vedaldi, and Zisserman 2014), or a mixed approach. A summary can be found in Samek, Wiegand, and Müller (2018) and Alber et al. (2019).
- The Bidirectional Encoder Representations from Transformers (BERT) family of models leads to high-performance models in Natural Language Processing. The exBERT method (Hoover, Strobelt, and Gehrmann 2020) is designed to visualize the activation of attention heads in this model.
Of course, the list of model classes with dedicated collections of model-explanation and/or diagnostics methods is much longer. This variety of model-specific approaches does lead to issues, though. For instance, one cannot easily compare explanations for two models with different structures. Also, every time a new architecture or a new ensemble of models is proposed, one needs to look for new methods of model exploration. Finally, no tools for model explanation or diagnostics may be immediately available for brand-new models.
For these reasons, in our book we focus on model-agnostic techniques. In particular, we prefer not to assume anything about the model structure, as we may be dealing with a black-box model with an unspecified structure. Note that often we do not have access to model coefficients, but only to a specified Application Programming Interface (API) that allows querying remote models as, for example, in Microsoft Cognitive Services (Azure 2019). In that case, the only operation that we may be able to perform is the evaluation of a model on a specified set of data.
However, while we do not assume anything about the structure of the model, we will assume that the model operates on \(p\)-dimensional vector of explanatory variables/features and, for a single observation, it returns a single value (score/probability), which is a real number. This assumption holds for a broad range of models for data such as tabular data, images, text data, videos, etc. It may not be suitable for, e.g., models with memory-like sequence-to-sequence models (Sutskever, Vinyals, and Le 2014) or Long Short-Term Memory models (Hochreiter and Schmidhuber 1997) in which the model output depends also on sequence of previous inputs, or generative models that output text of images.
1.6 The structure of the book
This book is split into four major parts. In the first part, Introduction, we introduce notation, datasets, and models used in the book. In the second part, Instance-level Exploration, we present techniques for exploration and explanation of a model’s predictions for a single observation. In the third part, Dataset-level Exploration, we present techniques for exploration and explanation of a model for an entire dataset. In the fourth part, Use-case, we apply the methods presented in the previous parts to an example in which we want to assess the value of a football player. The structure of the second and the third part is presented in Figure 1.3.
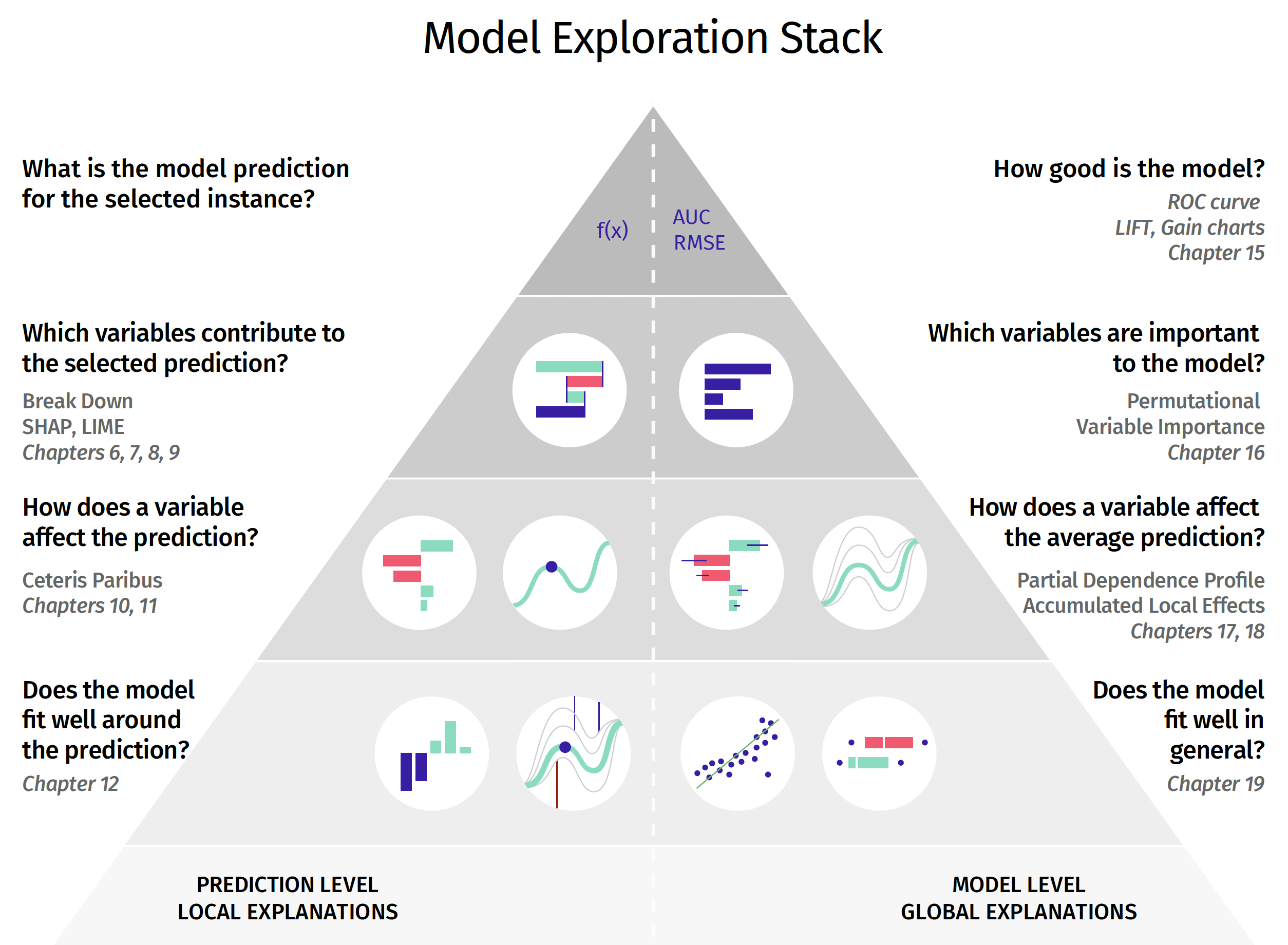
Figure 1.3: Model exploration methods presented in the book. The left-hand side (corresponding to the second part of the book) focuses on instance-level exploration, while the right-hand side (corresponding to the third part of the book) focuses on dataset-level exploration. Consecutive layers of the stack are linked with a deeper level of model exploration. The layers are linked with laws of model exploration introduced in Section 1.2.
In more detail, the first part of the book consists of Chapters 2–4. In Chapter 2, we provide a short introduction to the process of data exploration and model construction, together with notation and definition of key concepts that are used in consecutive chapters. Moreover, in Chapters 3.1 and 3.2, we provide a short description of R and Python tools and packages that are necessary to replicate the results presented in the book. Finally, in Chapter 4, we describe two datasets that are used throughout the book to illustrate the presented methods and tools.
The second part of the book focuses on instance-level explainers and consists of Chapters 6–13. Chapters 6–8 present methods that allow decomposing a model’s predictions into contributions corresponding to each explanatory variable. In particular, Chapter 6 introduces break-down (BD) for additive attributions for predictive models, while Chapter 7 extends this method to attributions that include interactions. Chapter 8 describes Shapley Additive Explanations (SHAP) (Lundberg and Lee 2017), an alternative method for decomposing a model’s predictions that is closely linked with Shapley values developed originally for cooperative games by Shapley (1953). Chapter 9 presents a different approach to the explanation of single-instance predictions. It is based on a local approximation of a black-box model by a simpler glass-box one. In this chapter, we discuss the Local-Interpretable Model-agnostic Explanations (LIME) method (Ribeiro, Singh, and Guestrin 2016). These chapters correspond to the second layer of the stack presented in Figure 1.3.
In Chapters 10–12 we present methods based on the ceteris-paribus (CP) profiles. The profiles show the change of model-based predictions induced by a change of a single explanatory-variable. The profiles are introduced in Chapter 10, while Chapter 11 presents a CP-profile-based measure that summarizes the impact of a selected variable on the model’s predictions. The measure can be used to determine the order of variables in model exploration. It is particularly important for models with large numbers of explanatory variables. Chapter 12 focuses on model diagnostics. It describes local-stability plots that are useful to investigate the sources of a poor prediction for a particular single observation. The final chapter of the second part, Chapter 13, compares various methods of instance-level exploration.
The third part of the book focuses on dataset-level exploration and consists of Chapters 14–19. The chapters present methods in the same order as shown in the right-hand side of Figure 1.3. In particular, Chapter 15 presents measures that are useful for the evaluation of the overall performance of a predictive model. Chapter 16 describes methods that are useful for the evaluation of an explanatory-variable’s importance. Chapters 17 and 18 introduce partial-dependence and accumulated-dependence methods for univariate exploration of a variable’s effect. These methods correspond to the third (from the top) layer of the right-hand side of the stack presented in Figure 1.3. The Chapter 19 summarises diagnostic techniques based on model residuals. The final chapter of this part of the book is Chapter 20 that summarises global techniques for model exploration.
The book is concluded with Chapter 21 that presents a worked-out example of model-development process in which we apply all the methods discussed in the second and third part of the book.
To make the exploration of the book easier, each chapter of the second and the third part of the book has the same structure:
- Section Introduction explains the goal of the method(s) presented in the chapter.
- Section Intuition explains the general idea underlying the construction of the method(s) presented in the chapter.
- Section Method shows mathematical or computational details related to the method(s). This subsection can be skipped if you are not interested in the details.
- Section Example shows an exemplary application of the method(s) with discussion of results.
- Section Pros and cons summarizes the advantages and disadvantages of the method(s). It also provides some guidance regarding when to use the method(s).
- Section Code snippets shows the implementation of the method(s) in R and Python. This subsection can be skipped if you are not interested in the implementation.
1.7 What is included in this book and what is not
The area of model exploration and explainability is quickly growing and is present in many different flavors. Instead of showing every existing method (is it really possible?), we rather selected a subset of consistent tools that form a good starting toolbox for model exploration. We mainly focus on the impact of the model exploration and explanation tools rather than on selected methods. We believe that by providing the knowledge about the potential of model exploration methods and about the language of model explanation, we will help the reader in improving the process of data modelling.
Taking this goal into account in this book, we do show
- how to determine which explanatory variables affect a model’s prediction for a single observation. In particular, we present the theory and examples of methods that can be used to explain prediction like break-down plots, ceteris-paribus profiles, local-model approximations, or Shapley values;
- techniques to examine predictive models as a whole. In particular, we review the theory and examples of methods that can be used to explain model performance globally, like partial-dependence plots or variable-importance plots;
- charts that can be used to present the key information in a quick way;
- tools and methods for model comparison;
- code snippets for R and Python that explain how to use the described methods.
On the other hand, in this book, we do not focus on
- any specific model. The techniques presented are model-agnostic and do not make any assumptions related to the model structure;
- data exploration. There are very good books on this topic by, for example, Grolemund and Wickham (2017) or McKinney (2012), or the excellent classic by Tukey (1977);
- the process of model building. There are also very good books on this topic by, for instance, Venables and Ripley (2002), James et al. (2014), or Efron and Hastie (2016);
- any particular tools for model building. These are discussed, for instance, by Kuhn and Johnson (2013).
1.8 Acknowledgements
This book has been prepared by using the bookdown package (Xie 2018), created thanks to the amazing work of Yihui Xie. A live version of this book is available at the GitHub repository https://github.com/pbiecek/ema. If you find any error, typo, or inaccuracy in the book, we will be grateful for your feedback at this website.
Figures and tables have been created mostly in the R language for statistical computing (R Core Team 2018) with numerous libraries that support predictive modelling. Just to name a few packages frequently used in this book: randomForest (Liaw and Wiener 2002), ranger (Wright and Ziegler 2017), rms (Harrell Jr 2018), gbm (Ridgeway 2017), or caret (Kuhn 2008). For statistical graphics, we have used the ggplot2 package (Wickham 2009). For model governance, we have used archivist (Biecek and Kosinski 2017). Examples in Python were added thanks to the fantastic work of Hubert Baniecki and Wojciech Kretowicz, who develop and maintain the dalex library. Most of the presented examples concern models built in the sklearn library (Pedregosa et al. 2011). The plotly library (Plotly Technologies Inc. 2015) is used to visualize the results.
We would like to thank everyone who contributed with feedback, found typos, or ignited discussions while the book was being written, including GitHub contributors: Rees Morrison, Alicja Gosiewska, Kasia Pekala, Hubert Baniecki, Asia Henzel, Anna Kozak, Agile Bean, Wojciech Kretowicz, Tuomo Kalliokoski, and Xiaochi Liu. We would like to acknowledge the anonymous reviewers, whose comments helped us to improve the contents of the book. We thank Jeff Webb, Riccardo De Bin, Patricia Martinkova, and Ziv Shkedy for their encouraging reviews. We are very grateful to John Kimmel from Chapman & Hall/CRC Press for his editorial assistance and patience.
Przemek’s work on model interpretability started during research trips within the RENOIR (H2020 grant no. 691152) secondments to Nanyang Technological University (Singapour) and Davis University of California (USA). He would like to thank Prof. Janusz Holyst for the chance to take part in this project. Przemek would also like to thank Prof. Chris Drake for her hospitality. This book would have never been created without the perfect conditions that Przemek found at Chris’s house in Woodland. Last but not least, Przemek would like to thank colleagues from the MI2DataLab and Samsung Research and Development Institute Poland for countless inspiring discussions related to Responsible Artificial Intelligence and Human Oriented Machine Learning.
Tomasz would like to thank colleagues from the Data Science Institute of Hasselt University and from the International Drug Development Institute (IDDI) for their support that allowed him finding the time to work on the book.
References
Alber, Maximilian, Sebastian Lapuschkin, Philipp Seegerer, Miriam Hägele, Kristof T. Schütt, Grégoire Montavon, Wojciech Samek, Klaus-Robert Müller, Sven Dähne, and Pieter-Jan Kindermans. 2019. “iNNvestigate Neural Networks!” Journal of Machine Learning Research 20 (93): 1–8. http://jmlr.org/papers/v20/18-540.html.
Azure. 2019. Microsoft Cognitive Services. https://azure.microsoft.com/en-en/services/cognitive-services/.
Bach, Sebastian, Alexander Binder, Grégoire Montavon, Frederick Klauschen, Klaus-Robert Müller, and Wojciech Samek. 2015. “On pixel-wise explanations for non-linear classifier decisions by layer-Wise relevance propagation.” Edited by Oscar Deniz Suarez. Plos One 10 (7): e0130140. https://doi.org/10.1371/journal.pone.0130140.
Biecek, Przemyslaw, and Marcin Kosinski. 2017. “archivist: An R Package for Managing, Recording and Restoring Data Analysis Results.” Journal of Statistical Software 82 (11): 1–28. https://doi.org/10.18637/jss.v082.i11.
Breiman, Leo. 2001b. “Statistical modeling: The two cultures.” Statistical Science 16 (3): 199–231. https://doi.org/10.1214/ss/1009213726.
Breiman, Leo, Adele Cutler, Andy Liaw, and Matthew Wiener. 2018. randomForest: Breiman and Cutler’s Random Forests for Classification and Regression. https://CRAN.R-project.org/package=randomForest.
Casey, Bryan, Ashkon Farhangi, and Roland Vogl. 2019. “Rethinking explainable machines: The GDPR’s Right to Explanation debate and the rise of algorithmic audits in enterprise.” Berkeley Technology Law Journal 34: 143–88.
Dastin, Jeffrey. 2018. “Amazon Scraps Secret AI Recruiting Tool That Showed Bias Against Women.” Reuters. https://www.reuters.com/article/us-amazon-com-jobs-automation-insight-idUSKCN1MK08G.
Diaz, Mark, Isaac Johnson, Amanda Lazar, Anne Marie Piper, and Darren Gergle. 2018. “Addressing Age-Related Bias in Sentiment Analysis.” In Proceedings of the 2018 Chi Conference on Human Factors in Computing Systems, 412:1–412:14. Chi ’18. Montreal QC, Canada: ACM. https://doi.org/10.1145/3173574.3173986.
Dobson, A. J. 2002. Introduction to Generalized Linear Models (2nd Ed.). Boca Raton, FL: Chapman; Hall/CRC.
Donizy, Piotr, Przemyslaw Biecek, Agnieszka Halon, and Rafal Matkowski. 2016. “BILLCD8 – a Multivariable Survival Model as a Simple and Clinically Useful Prognostic Tool to Identify High-Risk Cutaneous Melanoma Patients.” Anticancer Research 36 (September): 4739–48.
Duffy, Clare. 2019. “Apple co-founder Steve Wozniak says Apple Card discriminated against his wife.” CNN Business. https://edition.cnn.com/2019/11/10/business/goldman-sachs-apple-card-discrimination/index.html.
Efron, Bradley, and Trevor Hastie. 2016. Computer Age Statistical Inference: Algorithms, Evidence, and Data Science (1st Ed.). New York, NY: Cambridge University Press.
Ehrlinger, John. 2016. ggRandomForests: Exploring Random Forest Survival. https://arxiv.org/abs/1612.08974.
Faraway, Julian. 2005. Linear Models with R (1st Ed.). Boca Raton, Florida: Chapman; Hall/CRC. https://cran.r-project.org/doc/contrib/Faraway-PRA.pdf.
Foster, David. 2017. XgboostExplainer: An R Package That Makes Xgboost Models Fully Interpretable. https://github.com/AppliedDataSciencePartners/xgboostExplainer/.
Galecki, A., and T. Burzykowski. 2013. Linear Mixed-Effects Models Using R: A Step-by-Step Approach. New York, NY: Springer-Verlag New York.
GDPR. 2018. The EU General Data Protection Regulation (GDPR) is the most important change in data privacy regulation in 20 years. https://eugdpr.org/.
Goodman, Bryce, and Seth Flaxman. 2017. “European Union Regulations on Algorithmic Decision-Making and a ‘Right to Explanation’.” AI Magazine 38 (3): 50–57. https://doi.org/10.1609/aimag.v38i3.2741.
Grolemund, Garrett, and Hadley Wickham. 2017. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. O’Reilly Media. http://r4ds.had.co.nz/.
Harrell Jr, Frank E. 2018. Rms: Regression Modeling Strategies. https://CRAN.R-project.org/package=rms.
Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. “Long Short-Term Memory.” Neural Computation 9 (8): 1735–80. https://doi.org/10.1162/neco.1997.9.8.1735.
Hoover, Benjamin, Hendrik Strobelt, and Sebastian Gehrmann. 2020. “ExBERT: A Visual Analysis Tool to Explore Learned Representations in Transformer Models.” In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics: System Demonstrations, 187–96. Online: Association for Computational Linguistics. https://www.aclweb.org/anthology/2020.acl-demos.22.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2014. An Introduction to Statistical Learning: With Applications in R. New York, NY: Springer.
Karbowiak, Ewelina, and Przemyslaw Biecek. 2019. EIX: Explain Interactions in Gradient Boosting Models. https://CRAN.R-project.org/package=EIX.
Kuhn, Max. 2008. “Building Predictive Models in R Using the Caret Package.” Journal of Statistical Software 28 (5): 1–26. https://doi.org/10.18637/jss.v028.i05.
Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York, NY: Springer. http://appliedpredictivemodeling.com/.
Larson, Jeff, Surya Mattu, Lauren Kirchner, and Julia Angwin. 2016. “How We Analyzed the COMPAS Recidivism Algorithm.” ProPublica. https://www.propublica.org/article/how-we-analyzed-the-compas-recidivism-algorithm.
Lazer, David, Ryan Kennedy, Gary King, and Alessandro Vespignani. 2014. “The Parable of Google Flu: Traps in Big Data Analysis.” Science 343 (6176): 1203–5. https://doi.org/10.1126/science.1248506.
Liaw, Andy, and Matthew Wiener. 2002. “Classification and regression by randomForest.” R News 2 (3): 18–22. http://CRAN.R-project.org/doc/Rnews/.
Lundberg, Scott M, and Su-In Lee. 2017. “A Unified Approach to Interpreting Model Predictions.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 4765–74. Montreal: Curran Associates. http://papers.nips.cc/paper/7062-a-unified-approach-to-interpreting-model-predictions.pdf.
Molnar, Christoph. 2019. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable.
Olhede, S., and P. Wolfe. 2018. “The AI spring of 2018.” Significance 15 (3): 6–7. https://doi.org/https://doi.org/10.1111/j.1740-9713.2018.01140.x.
O’Neil, Cathy. 2016. Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy. New York, NY: Crown Publishing Group.
Paluszynska, Aleksandra, and Przemyslaw Biecek. 2017. RandomForestExplainer: A Set of Tools to Understand What Is Happening Inside a Random Forest. https://github.com/MI2DataLab/randomForestExplainer.
Pedregosa, F., G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, et al. 2011. “Scikit-Learn: Machine Learning in Python.” Journal of Machine Learning Research 12: 2825–30.
Plotly Technologies Inc. 2015. Collaborative Data Science. Montreal, QC. https://plot.ly.
R Core Team. 2018. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. 2016. “"Why should I trust you?": Explaining the Predictions of Any Classifier.” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Kdd San Francisco, ca, 1135–44. New York, NY: Association for Computing Machinery.
Ridgeway, Greg. 2017. Gbm: Generalized Boosted Regression Models. https://CRAN.R-project.org/package=gbm.
Ross, Casey, and Ike Swetliz. 2018. “IBM’s Watson supercomputer recommended ‘unsafe and incorrect’ cancer treatments, internal documents show.” Statnews. https://www.statnews.com/2018/07/25/ibm-watson-recommended-unsafe-incorrect-treatments/.
Ruiz, Javier. 2018. “Machine learning and the right to explanation in GDPR.” Open Rights Group. https://www.openrightsgroup.org/blog/2018/machine-learning-and-the-right-to-explanation-in-gdpr.
Salzberg, Steven. 2014. “Why Google Flu is a failure.” Forbes. https://www.forbes.com/sites/stevensalzberg/2014/03/23/why-google-flu-is-a-failure/.
Samek, Wojciech, Thomas Wiegand, and Klaus-Robert Müller. 2018. Explainable Artificial Intelligence: Understanding, Visualizing and Interpreting Deep Learning Models. ITU Journal: ICT Discoveries - Special Issue 1 - the Impact of Artificial Intelligence (AI) on Communication Networks and Services. Vol. 1. https://www.itu.int/en/journal/001/Pages/05.aspx.
Shapley, Lloyd S. 1953. “A Value for n-Person Games.” In Contributions to the Theory of Games Ii, edited by Harold W. Kuhn and Albert W. Tucker, 307–17. Princeton: Princeton University Press.
Sheather, Simon. 2009. A Modern Approach to Regression with R. Springer Texts in Statistics. New York, NY: Springer.
Simonyan, Karen, Andrea Vedaldi, and Andrew Zisserman. 2014. “Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps.” In ICLR (Workshop Poster), edited by Yoshua Bengio and Yann LeCun. http://dblp.uni-trier.de/db/conf/iclr/iclr2014w.html#SimonyanVZ13.
Sutskever, Ilya, Oriol Vinyals, and Quoc V. Le. 2014. “Sequence to Sequence Learning with Neural Networks.” In NIPS, edited by Zoubin Ghahramani, Max Welling, Corinna Cortes, Neil D. Lawrence, and Kilian Q. Weinberger, 3104–12. http://dblp.uni-trier.de/db/conf/nips/nips2014.html#SutskeverVL14.
Tukey, John W. 1977. Exploratory Data Analysis. Boston, MA: Addison-Wesley.
Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with S (4th Ed.). New York, NY: Springer. http://www.stats.ox.ac.uk/pub/MASS4.
McKinney, Wes. 2012. Python for Data Analysis (1st Ed.). O’Reilly Media, Inc.
Wickham, Hadley. 2009. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. http://ggplot2.org.
Wright, Marvin N., and Andreas Ziegler. 2017. “ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R.” Journal of Statistical Software 77 (1): 1–17. https://doi.org/10.18637/jss.v077.i01.
Xie, Yihui. 2018. bookdown: Authoring Books and Technical Documents with R Markdown. https://CRAN.R-project.org/package=bookdown.