Rozdział 10 Przykład budowy dynamicznego modelu liniowego
10.1 Wprowadzenie
W skład dynamicznego modelu liniowego wchodzą następujące elementy:
trend
składnik sezonowości
składnik autoregresji
Do estymacji takiego modelu zostaną wykorzystane dodatkowe pakiety czyli takie
które nie są instalowane wraz z oprogramowaniem R. Pod linkiem można zapoznać się dokumentacją bibliotek bazowych.
Instalację pakietu wykonujemy tylko raz niezależnie od tego ile razy uruchomimy środowisko R.
install.packages("tseries")Wykonując powyższe polecenie zostanie zainstalowana biblioteka wraz z wymaganymi zależnościami (dodatkowe pakiety) jeśli takie są wymagane. Następnie należy taką bibliotekę załadować:
library("tseries")Inne podejście to odwoływanie się za każdym razem do wybranego pakietu który wcześniej został zainstalowany. Inaczej mówiąc, wskazujemy z jakiego pakietu chcemy wykorzystać funkcję. To rozwiązanie jest przydatne jeśli w dwóch różnych pakietach z których korzystamy występują takie same nazwy funkcji:
tseries::funkcja_z_pakietu_tseries( argumenty_funkcji )Aby wprowadzić dane dotyczące miesięcznej stopy bezrobocia w Polsce można wykonać poniższe polecenie:
b=c(
19.5, 19.4, 19.3, 19.1, 18.9, 18.7, 18.7, 19.0, 19.4, 19.4, 19.2, 18.7,
18.2, 18.0, 17.9, 17.7, 17.6, 17.3, 17.3, 17.6, 18.0, 18.0, 17.8, 17.2,
16.5, 16.0, 15.7, 15.5, 15.2, 14.9, 14.8, 14.9, 15.1, 14.9, 14.4, 13.7,
13.0, 12.4, 12.2, 11.9, 11.6, 11.3, 11.3, 11.4, 11.7, 11.5, 11.1, 10.5,
10.0, 9.6, 9.4, 9.1, 8.9, 8.8, 9.1, 9.5, 10.5, 10.9, 11.2, 11.0,
10.8, 10.7, 10.8, 10.8, 10.9, 11.1, 11.4, 11.9, 12.7, 13.0, 12.9, 12.3,
11.9
)Ponieważ powyższe dane (procenty) dotyczą okresu od 05.2004 do 05.2010 więc przekształcimy zmienną b
(zapisną w postaci wektora zmiennych) w szereg czasowy. Do budowy szeregu czasowego zostanie wykorzystana funkcja ts.
bezrob <- ts(b,start=c(2004,5),freq=12)par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(bezrob,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(bezrob,xlab="czas",ylab="stopa bezrobocia",col="SteelBlue",lwd=2,las=1)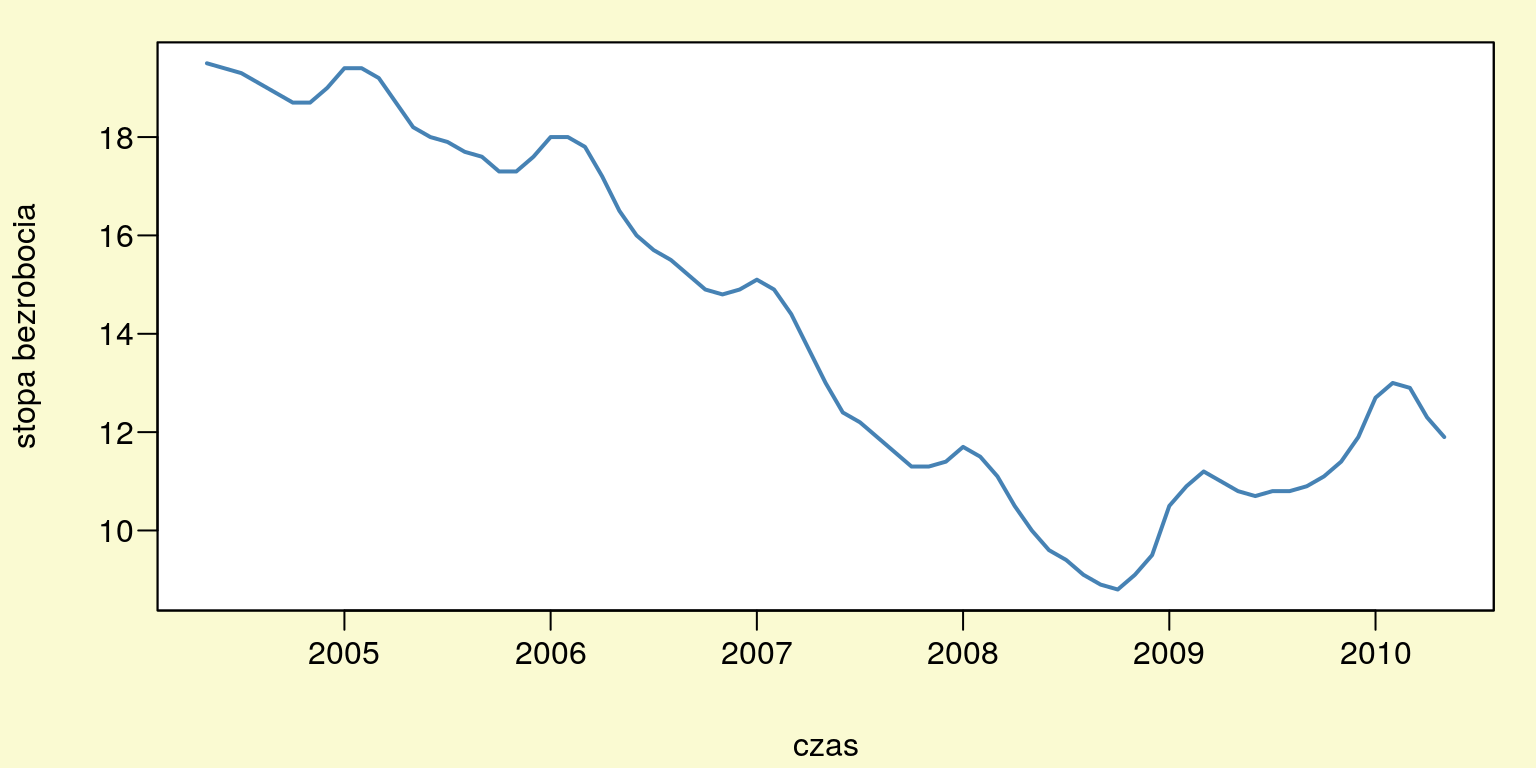
Rysunek 10.1: Stopa bezrobocia w Polsce od 0.5.2004 do 0.5.2010.
10.2 Badanie wewnętrznej struktury procesu
10.2.1 Trend
W pierwszym kroku należy ustalić, czy w szeregu czasowym (rys. 10.1) występuje tendencja rozwojowa czyli trend. Jeśli dojdziemy do wniosku, że występuje trend należy zbudować kilka wielomianowych modeli trendu a następnie dokonać wyboru najlepszego modelu. Wybór wielomianu możemy dokonać za pomocą analizy wariancji ANOVA lub kryterium informacyjnego AIC.
t1 <- ts(1:length(bezrob),start=c(2004,5),freq=12)
t2 <- ts(t1^2,start=c(2004,5),freq=12)
t3 <- ts(t1^3,start=c(2004,5),freq=12)
t4 <- ts(t1^4,start=c(2004,5),freq=12)m1 <- lm(bezrob~t1) # wielomian stopnia pierwszego
m2 <- lm(bezrob~t1+t2) # wielomian stopnia drugiego
m3 <- lm(bezrob~t1+t2+t3) # wielomian stopnia trzeciego
m4 <- lm(bezrob~t1+t2+t3+t4) # wielomian stopnia czwartego# porównanie modelu trendu m1 i m2:
anova(m1,m2)## Analysis of Variance Table
##
## Model 1: bezrob ~ t1
## Model 2: bezrob ~ t1 + t2
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 71 176.96
## 2 70 109.76 1 67.202 42.86 8.284e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# porównanie modelu trendu m2 i m3:
anova(m2,m3)## Analysis of Variance Table
##
## Model 1: bezrob ~ t1 + t2
## Model 2: bezrob ~ t1 + t2 + t3
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 70 109.756
## 2 69 26.572 1 83.183 216 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# porównanie modelu trendu m3 i m4:
anova(m3,m4)## Analysis of Variance Table
##
## Model 1: bezrob ~ t1 + t2 + t3
## Model 2: bezrob ~ t1 + t2 + t3 + t4
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 69 26.572
## 2 68 26.569 1 0.0034355 0.0088 0.9256Tak więc najlepszym modelem trendu okazał się wielomian stopnia trzeciego. Do takiego samego wniosku dochodzimy porównując kryteria informacyjne AIC wszystkich modeli.
AIC(m1,m2,m3,m4)## df AIC
## m1 3 277.8030
## m2 4 244.9342
## m3 5 143.3919
## m4 6 145.382510.2.2 Sezonowość
Aby ocenić czy w badanym szeregu czasowym występują wahania sezonowe trzeba oszacować model trendu wraz ze zmiennymi sezonowymi. Jeśli przynajmniej jeden parametr przy zmiennej zero-jedynkowej okaże się istotny możemy sądzić, że w szeregu występuje sezonowość.
# zmienne sezonowe: zero-jedynkowe:
month <- ts(forecast::seasonaldummy(bezrob),start=c(2004,5),freq=12)# model z trendem i sezonowością:
s_dyn <- lm(bezrob~t1+t2+t3+month)
# podsumowanie modelu z trendem i sezonowością:
summary(s_dyn)##
## Call:
## lm(formula = bezrob ~ t1 + t2 + t3 + month)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.23729 -0.31580 -0.01533 0.36128 0.82255
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.903e+01 3.153e-01 60.363 < 2e-16 ***
## t1 1.258e-01 2.853e-02 4.410 4.54e-05 ***
## t2 -1.280e-02 8.917e-04 -14.357 < 2e-16 ***
## t3 1.372e-04 7.927e-06 17.311 < 2e-16 ***
## monthJan 5.935e-01 2.815e-01 2.109 0.0393 *
## monthFeb 7.138e-01 2.816e-01 2.535 0.0140 *
## monthMar 5.934e-01 2.818e-01 2.106 0.0396 *
## monthApr 1.149e-01 2.821e-01 0.407 0.6854
## monthMay -2.402e-01 2.721e-01 -0.883 0.3811
## monthJun -2.513e-01 2.829e-01 -0.888 0.3780
## monthJul -2.861e-01 2.824e-01 -1.013 0.3152
## monthAug -3.891e-01 2.820e-01 -1.380 0.1730
## monthSep -4.612e-01 2.818e-01 -1.637 0.1071
## monthOct -5.365e-01 2.816e-01 -1.905 0.0617 .
## monthNov -3.658e-01 2.815e-01 -1.300 0.1988
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4874 on 58 degrees of freedom
## Multiple R-squared: 0.9842, Adjusted R-squared: 0.9803
## F-statistic: 257.4 on 14 and 58 DF, p-value: < 2.2e-16Ponieważ kilka zmiennych sezonowych jest istotnych statystycznie należy stwierdzić, że w badanym procesie występują wahania sezonowe.
10.2.3 Stopień autoregresji – funkcja PACF
Aby ocenić stopień autoregresji dynamicznego modelu liniowego należy sprawdzić czy w procesie reszt (modelu z trendem i sezonowością) występuje autokorelacja reszt. Można tego dokonać na podstawie funcji PACF (rys. 10.2) na poziomie istotności \(\alpha = 0,05\) (przerywana linia pozioma).
rs <- ts(resid(s_dyn),start=c(2004,5),freq=12)par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
pacf(rs,plot=T)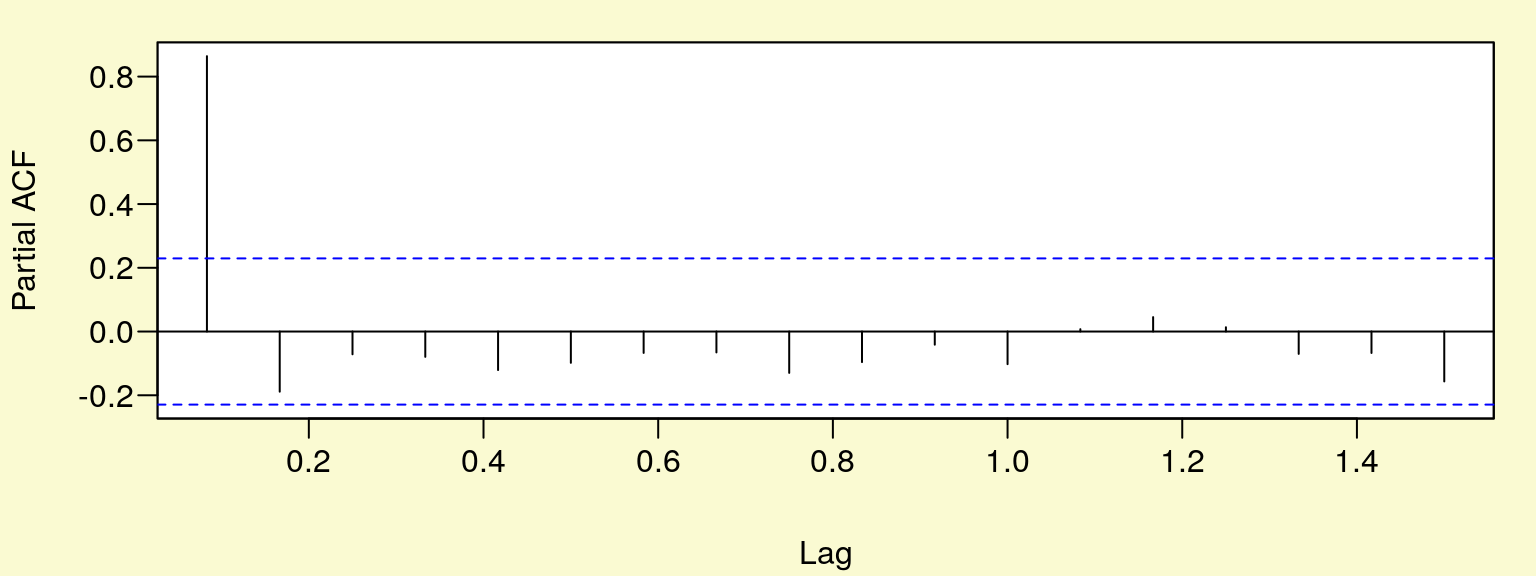
Rysunek 10.2: Funkcja autokorelacji cząstkowej.
Jak widać na (rys. 10.2) występuje rząd autokorelacji \(p = 1\).
10.2.4 Stopień integracji – test ADF/PP
Jeśli otrzymane reszty (rys. 10.3) na podstawie modelu z trendem i sezonowością są niestacjonarne (występuje pierwiastk jednostkowy) należy wówczas rząd autoregresji (w dynamicznym modelu liniowym) powiększyć o liczbę \(d\) czyli liczbę pierwiastków jednostkowych. Do sprawdzenia hipotezy o występowaniu pierwiastka jednostkowego możemy posłużyć się rozszerzonym testem Dickey’a-Fullera.
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(rs,type="l",col="SteelBlue")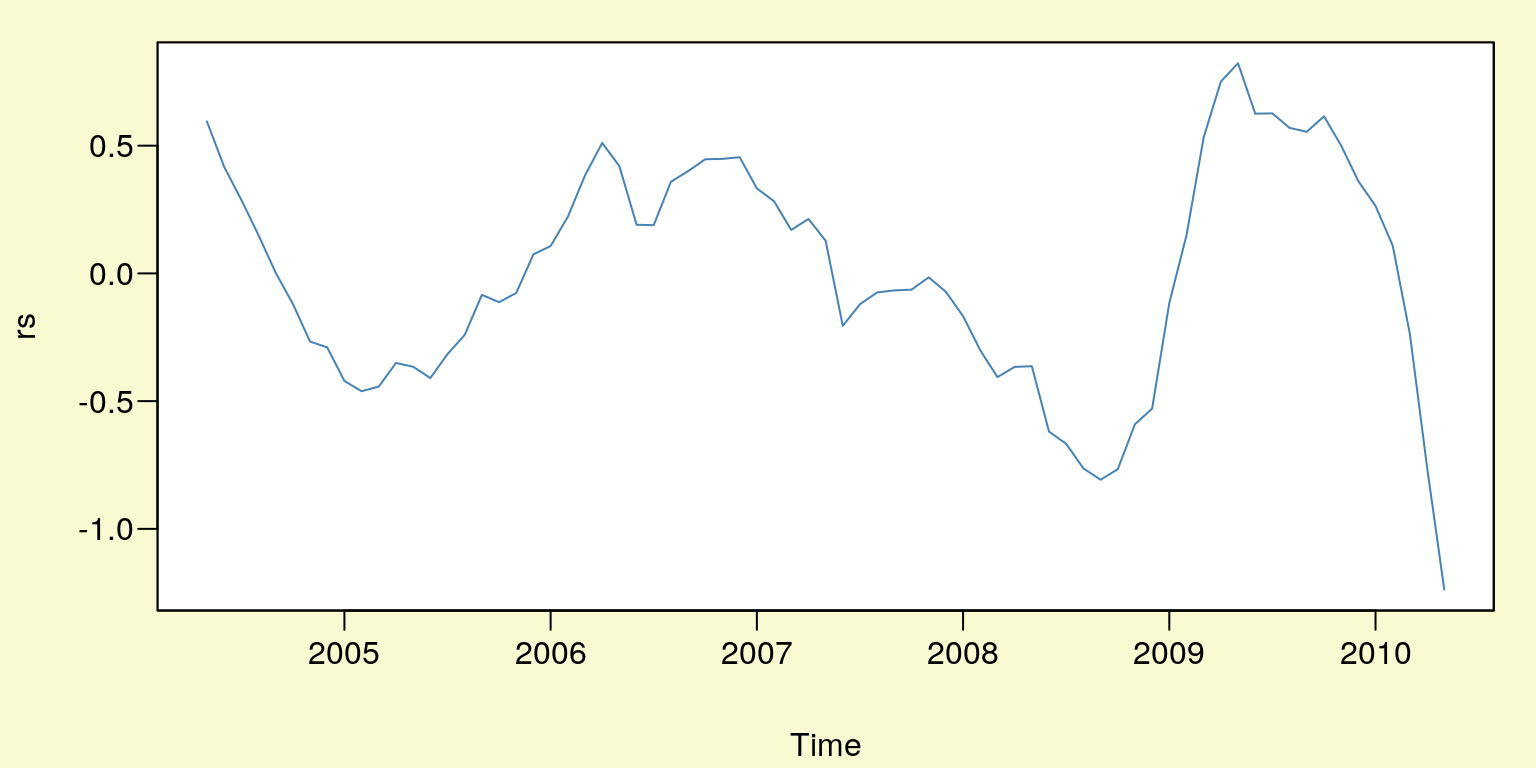
Rysunek 10.3: Reszty modelu z trendem i sezonowością \(rs_t\).
tseries::adf.test(rs)##
## Augmented Dickey-Fuller Test
##
## data: rs
## Dickey-Fuller = -2.6101, Lag order = 4, p-value = 0.3268
## alternative hypothesis: stationaryPonieważ w teście ADF p-value jest równe \(0,3268\) należy przyjąć, że w procesie \(rs_t\) występuje pierwiastk jednostkowy \(d = 1\). Skoro szereg \(rs_t\) jest niestacjonarny należy sprawdzić czy w procesie \(\Delta rs_t = rs_t - rs_{t-1}\) również występuje pierwiastek jednostkowy. A więc czy szereg \(rs_t\) jest zintegrowany w stopniu drugin tzn. \(I(2)\).
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(diff(rs),type="l",col="SteelBlue")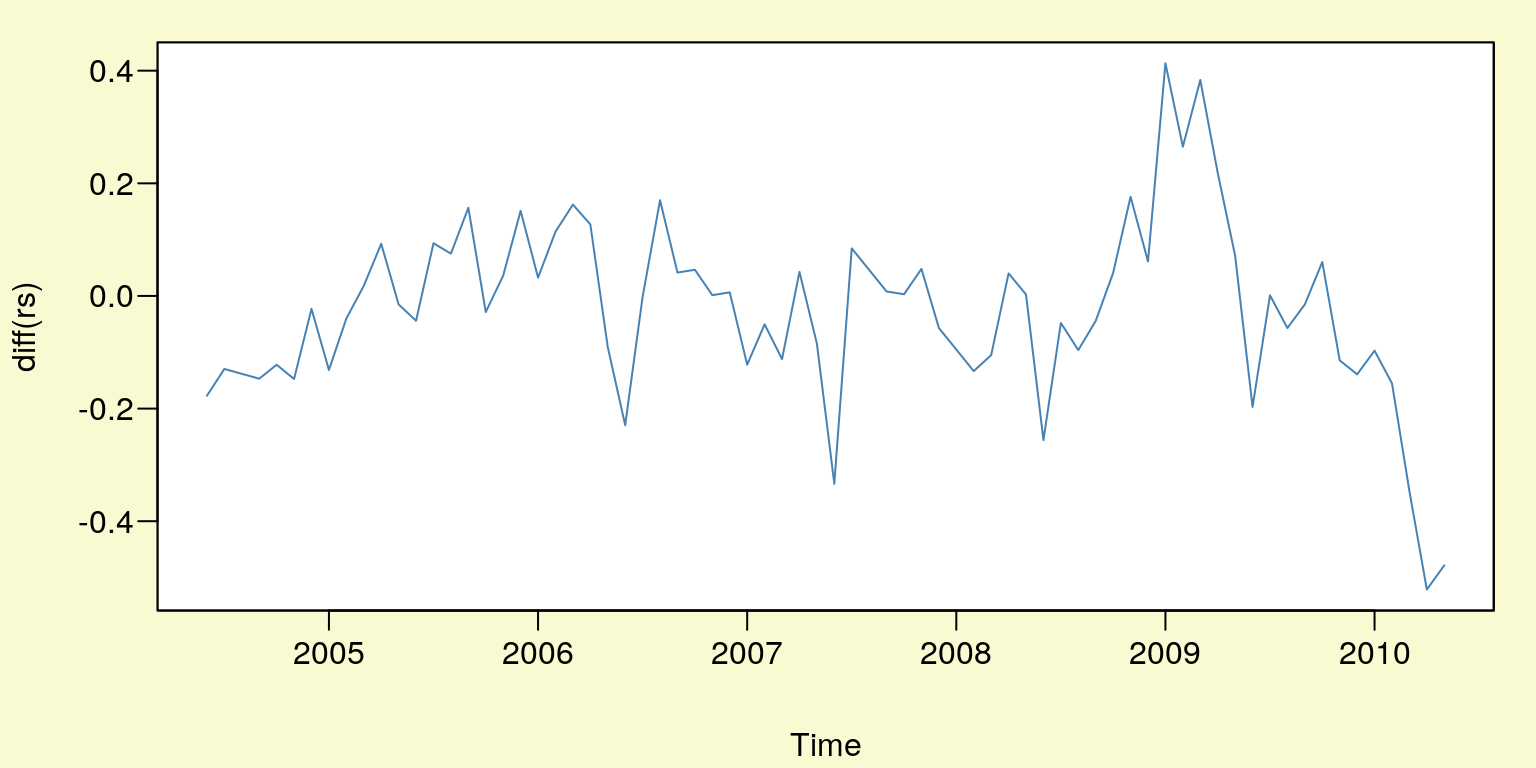
Rysunek 10.4: Reszty modelu po jednokrotnym różnicowaniu \(rs_t\) .
tseries::adf.test(diff(rs))##
## Augmented Dickey-Fuller Test
##
## data: diff(rs)
## Dickey-Fuller = -1.7534, Lag order = 4, p-value = 0.6757
## alternative hypothesis: stationaryTak więc szereg \(rs_t\) jest zintegrowany w stopniu drugim (p-value = \(0,6757\)), badamy więc czy jest również zintegrowany w stopniu trzecim.
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(diff(diff(rs)),type="l",col="SteelBlue")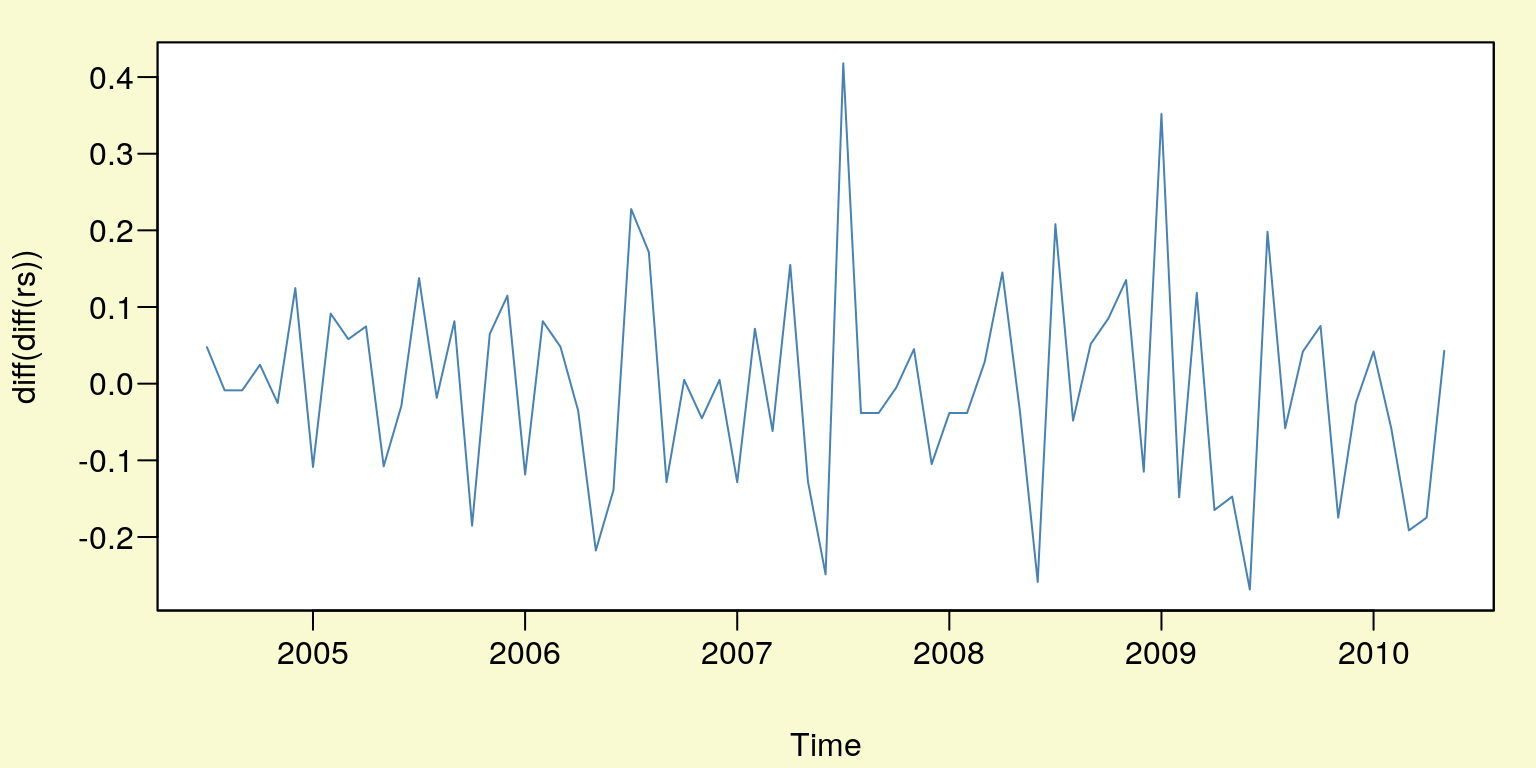
Rysunek 10.5: Reszty modelu po dwukrotnym różnicowaniu \(rs_t\).
tseries::adf.test(diff(diff(rs)))## Warning in tseries::adf.test(diff(diff(rs))): p-value smaller than printed
## p-value##
## Augmented Dickey-Fuller Test
##
## data: diff(diff(rs))
## Dickey-Fuller = -4.4611, Lag order = 4, p-value = 0.01
## alternative hypothesis: stationaryZatem dla \(H_0: I(3)\) p-value jest równe \(0,01\). Czyli szereg \(\Delta\Delta rs_t\) jest stacjonarny i na tym kończymy procedurę oceny zintegrowania szeregu \(rs_t\). Rząd autoregresji w dynamicznym modelu liniowym będzie więc wynosił: \(p + d = 1 + 2 = 3\). Innym testem do oceny istnienia pierwiastka jednostkowego jest test Phillipsa-Perrona.
tseries::pp.test(rs)##
## Phillips-Perron Unit Root Test
##
## data: rs
## Dickey-Fuller Z(alpha) = -8.8842, Truncation lag parameter = 3,
## p-value = 0.5915
## alternative hypothesis: stationarytseries::pp.test(diff(rs))##
## Phillips-Perron Unit Root Test
##
## data: diff(rs)
## Dickey-Fuller Z(alpha) = -22.395, Truncation lag parameter = 3,
## p-value = 0.02967
## alternative hypothesis: stationarytseries::pp.test(diff(diff(rs)))## Warning in tseries::pp.test(diff(diff(rs))): p-value smaller than printed
## p-value##
## Phillips-Perron Unit Root Test
##
## data: diff(diff(rs))
## Dickey-Fuller Z(alpha) = -80.495, Truncation lag parameter = 3,
## p-value = 0.01
## alternative hypothesis: stationaryW oprogramowaniu R możemy również skorzystać z szeregu innych testów dotyczących pierwiastka jednostkowego. Są one dostępne w następujących paczkach:
uroot, urca, fUnitRoots.
10.3 Weryfikacja modelu
10.3.1 Estymacja dynamicznego modelu liniowego
library("dyn")
# estymacja modelu:
m_dyn <- dyn$lm(bezrob~t1+t2+t3+month+
stats::lag(bezrob,-1)+stats::lag(bezrob,-2)+stats::lag(bezrob,-3))
# podsumowanie modelu
summary(m_dyn)##
## Call:
## lm(formula = dyn(bezrob ~ t1 + t2 + t3 + month + stats::lag(bezrob,
## -1) + stats::lag(bezrob, -2) + stats::lag(bezrob, -3)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.218117 -0.055641 0.000827 0.051768 0.272502
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.716e+00 6.131e-01 2.799 0.007172 **
## t1 8.245e-03 1.169e-02 0.705 0.483721
## t2 -8.612e-04 5.818e-04 -1.480 0.144833
## t3 9.069e-06 5.615e-06 1.615 0.112309
## month1 6.025e-02 6.328e-02 0.952 0.345409
## month2 -5.624e-01 7.525e-02 -7.474 8.69e-10 ***
## month3 -6.115e-01 1.129e-01 -5.417 1.58e-06 ***
## month4 -6.728e-01 8.569e-02 -7.852 2.18e-10 ***
## month5 -3.977e-01 9.862e-02 -4.033 0.000181 ***
## month6 -1.633e-01 8.482e-02 -1.925 0.059724 .
## month7 -4.991e-02 7.443e-02 -0.671 0.505471
## month8 -3.025e-01 6.263e-02 -4.829 1.25e-05 ***
## month9 -3.062e-01 7.022e-02 -4.361 6.14e-05 ***
## month10 -3.064e-01 6.484e-02 -4.725 1.79e-05 ***
## month11 -7.425e-02 6.629e-02 -1.120 0.267842
## stats::lag(bezrob, -1) 1.478e+00 1.297e-01 11.400 9.31e-16 ***
## stats::lag(bezrob, -2) -1.947e-01 2.453e-01 -0.794 0.430944
## stats::lag(bezrob, -3) -3.605e-01 1.444e-01 -2.497 0.015719 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1006 on 52 degrees of freedom
## (6 observations deleted due to missingness)
## Multiple R-squared: 0.9993, Adjusted R-squared: 0.9991
## F-statistic: 4551 on 17 and 52 DF, p-value: < 2.2e-16p_dyn <- predict(m_dyn)par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(bezrob,type='l',lwd=4,col='SteelBlue')
lines(p_dyn,lwd=2,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,2),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))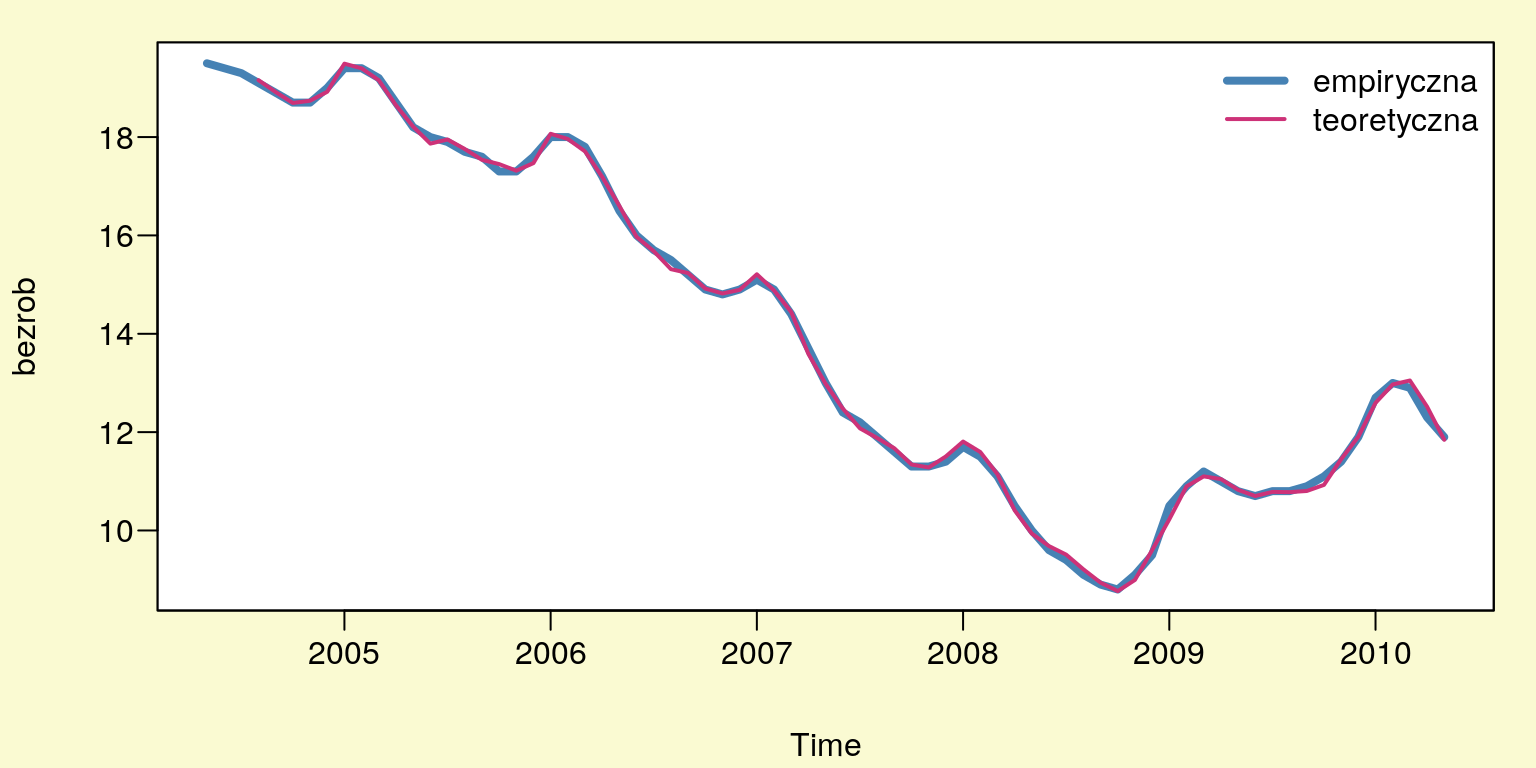
Rysunek 10.6: Wykres wartości empirycznych i teoretycznych.
10.3.2 Ocena jakości modelu
Dokonując oceny jakości modelu należy zwrócić uwagę na wysoką wartość \(R^2\) który wynosi \(0,9993\). Oznacza to, że w \(99,93\%\) została wyjaśniona zmienność zmiennej zależnej (stopa bezrobocia) przez model. Na podstawie oszacowanego błędu standardowego reszt \(Se\), który jest równy \(0,1006\) możemy stwierdzić, że średnio o \(10,06\%\) odchylają się wartości rzeczywiste stopy bezrobocia od wartości teoretycznych – oszacowanych na podstawie modelu. Także test \(F\) wskazuje na dobre dopasowanie modelu (p-value = \(2,2e-16\)).
10.4 Diagnostyka modelu
10.4.1 Normalność procesu resztowego
Ocena normalności składnika resztowego została dokonana za pomocą testu Shapiro- Wilka oraz testu \(\chi^2\) w oparciu o procedurę zaproponowaną przez Doornika oraz Hansena.
r_dyn <- resid(m_dyn)
shapiro.test(r_dyn)##
## Shapiro-Wilk normality test
##
## data: r_dyn
## W = 0.98619, p-value = 0.6382Wysoka wartość p-value, która wynosi \(0,6382\) pozwala nam wnioskować, że na podstawie testu Shapiro-Wilka reszty mają rozkład normalny.
normwhn.test::normality.test1(as.matrix(r_dyn))## [1] "sk"
## [1] 0.3667684
## [1] "k"
## [1] 3.48438
## [1] "rtb1"
## [1] 0.3667684
## [1] "b2"
## [1] 3.48438
## [1] "z1"
## [1] 1.330065
## [1] "z2"
## [1] 0.9789823
## [1] "H0: data do not have skewness"
## [1] "pvalsk"
## [1] 0.1834968
## [1] "H0: data do not have negative skewness"
## [1] "pskneg"
## [1] 0.9082516
## [1] "H0: data do not have positive skewness"
## [1] "pskpos"
## [1] 0.09174841
## [1] "H0: data do not have kurtosis"
## [1] "pvalk"
## [1] 0.3275887
## [1] "H0: data do not have negative kurtosis"
## [1] "pkneg"
## [1] 0.8362056
## [1] "H0: data do not have positive kurtosis"
## [1] "pkpos"
## [1] 0.1637944
## [1] "H0: data are normally distributed"
## [1] "Ep"
## [,1]
## [1,] 2.727479
## [1] "dof"
## [1] 2
## [1] "sig.Ep"
## [,1]
## [1,] 0.2557027Również wynik testu \(\chi^2\) wskazuje, że nie ma podstaw do odrzucenia hipotezy zerowej
przy poziomie istotności \(\alpha = 0,05\). Należy więc stwierdzić, że proces resztowy ma
rozkład normalny. Wyniki obu testów potwierdzają też wykresy (rys. 10.7).
Do badania normalności zmiennych można wykorzystać także inne testy, które
są dostępne w środowisku R. Oto niektóre z nich: test
normalności Jarque-Bera – moments::jarque.test, test skośności D’Agostino – moments::agostino.test, test kurtozy Anscombe-Glynn – moments::anscombe.test.
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(density(r_dyn),lwd=4,col='SteelBlue')
curve(dnorm(x,mean(r_dyn),sd(r_dyn)),add=TRUE,lwd=2,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,2),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
qqnorm(r_dyn,col='SteelBlue'); qqline(r_dyn,col='violetred3')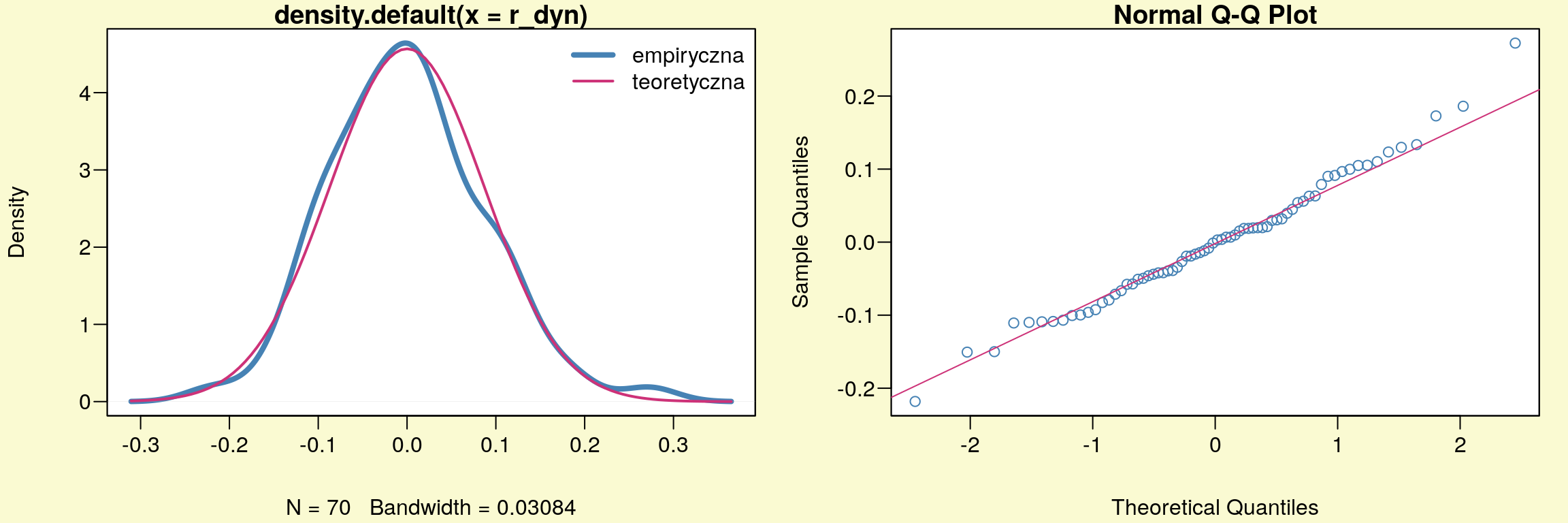
Rysunek 10.7: Graficzna diagnostyka normalności rozkładu reszt.
10.4.2 Autokorelacja procesu resztowego
Do oceny autokorelacji reszt można wykorzystać test autokorelacji Ljunga-Boxa,
który jest dostępny w paczce tseries. W tym teście dzięki opcji lag możemy badać
stopień autokorelacji dowolnego rzędu.
Box.test (r_dyn, lag= 1, type= "Ljung-Box")##
## Box-Ljung test
##
## data: r_dyn
## X-squared = 0.059179, df = 1, p-value = 0.8078par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
pacf(r_dyn,plot=T)## Warning in if (plot) {: warunek posiada długość > 1 i tylko pierwszy
## element będzie użyty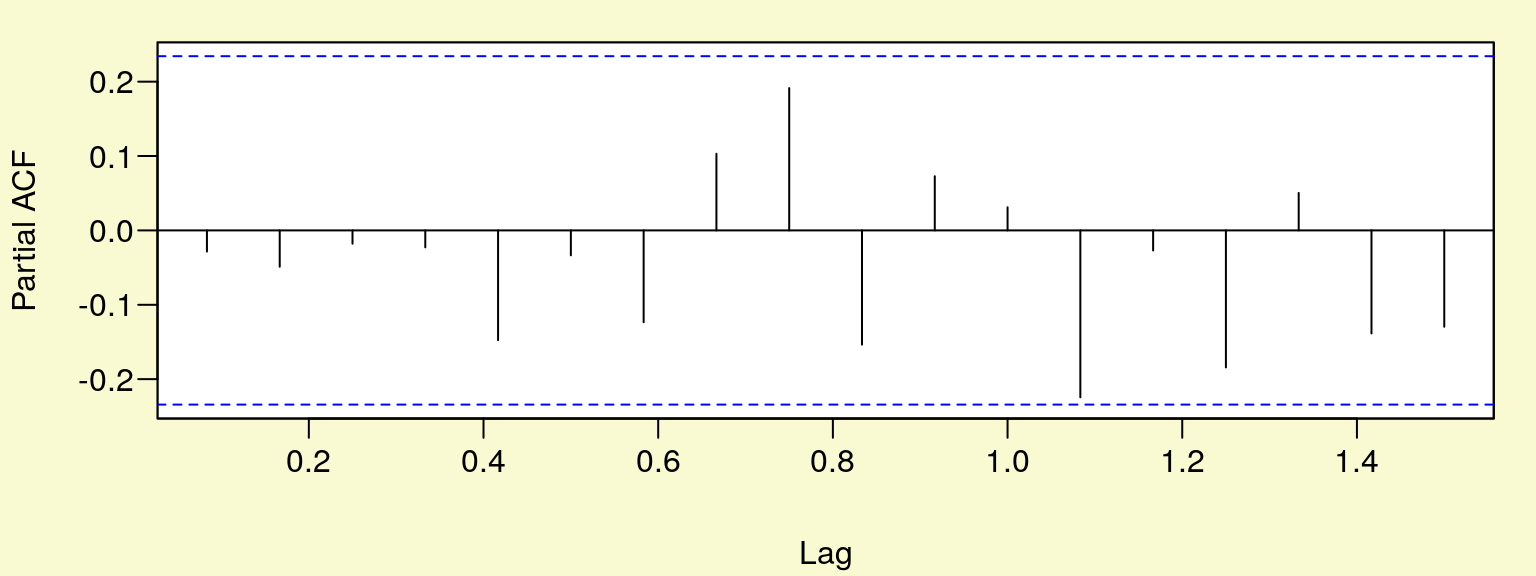
Rysunek 10.8: Funkcja autokorelacji cząstkowej reszt modelu.
Także test Quenouille’a na poziomoe istotności \(\alpha = 0,05\) (przerywane poziome
linie – rys. (10.8)) potwierdza brak zjawiska autokorelacji reszt. W oprogramowaniu R dostępne są też inne testy do badania tego zjawiska np. test Breuscha-Godfreya – lmtest::bgtest
oraz test Durbina-Watsona – lmtest::dwtest. Jednak
ten ostatni umożliwia badanie tylko autokorelacji rzędu pierwszego.
10.4.3 Heteroskedastyczność procesu resztowego
Ponieważ niejednorodność wariancji jest zjawiskiem nieporządanym należy więc zbadać czy występuje heteroskedastyczność w procesie reszt. Do tego celu można wykorzystać test Breusha-Pagana.
# test Koenkera:
lmtest::bptest(m_dyn)##
## studentized Breusch-Pagan test
##
## data: m_dyn
## BP = 22.774, df = 17, p-value = 0.1567# test Breusha-Pagana:
lmtest::bptest(m_dyn,studentize=F)##
## Breusch-Pagan test
##
## data: m_dyn
## BP = 28.29, df = 17, p-value = 0.04166# Cook i Weisberg [1983]:
lmtest::bptest(m_dyn,studentize=F,varformula =~fitted(m_dyn))##
## Breusch-Pagan test
##
## data: m_dyn
## BP = 1.7564, df = 1, p-value = 0.1851Na podstawie przeprowadzonych testów Breusha-Pagana możemy wnioskować, że
występuje homoskedastyczność reszt. Dzięki środowisku R mamy możliwość przeprowadzenia także innych testów np. test Harrisona-McCabea – lmtest::hmctest
lub test Goldfelda-Quandta – lmtest::gqtest.
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(r_dyn,col='SteelBlue')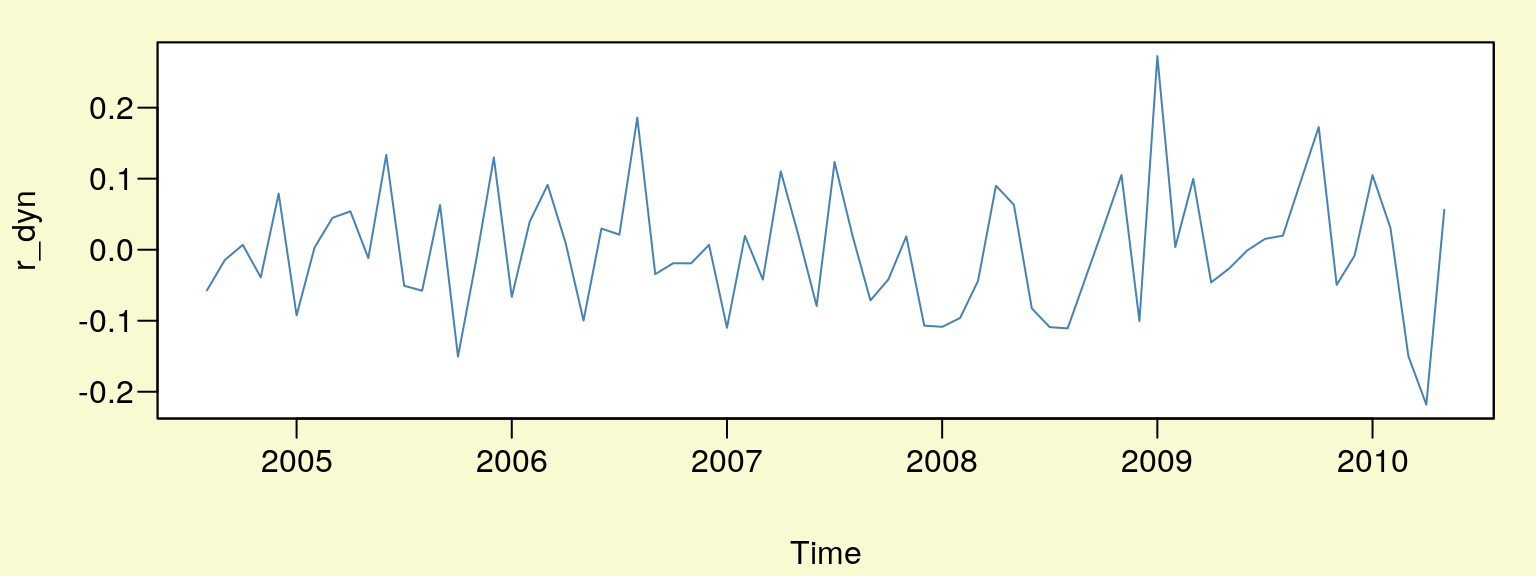
Rysunek 10.9: Reszty modelu.
10.4.4 Stabilność parametrów modelu
Do zbadania stabilności parametrów modelu można wykorzystać test Chowa. Jednak aby móc zastosować ten test należy określić punkt zwrotny, który podzieli cały
analizowany proces na dwie podpróby. Jeśli w tych dwóch podokresach parametry modeli nie będą się różniły, można wtedy przyjąć, że są one stabilne. W teście
strucchange::sctest jako punkt zwrotny należy podać ostatnią datę z pierwszej
podpróby. Tzn. jeśli za punkt zwrotny przyjmiemy 10.2008 (pierwsza data drugiej
podpróby) to dla opcji point trzeba podać 09.2008 (ostatnia data pierwszej podpróby).
# przygotowanie danych:
d <- cbind(bezrob,t1,t2,t3,month,
stats::lag(bezrob,k=-1),stats::lag(bezrob,k=-2),stats::lag(bezrob,k=-3))
d <- na.omit(d)
# test Chowa:
strucchange::sctest(bezrob~., data=d, type="Chow", point=c(2008,9))##
## Chow test
##
## data: bezrob ~ .
## F = 5.5201, p-value = 9.785e-06Innym testem, który bada stabilność parametrów modelu jest test CUSUM (cumulated sum of residuals) zwany także testem Harvey’a-Colliera. Jest on dostępny
w programie R po uprzednim wczytaniu biblioteki lmtest.
lmtest::harvtest(m_dyn)##
## Harvey-Collier test
##
## data: m_dyn
## HC = 0.36995, df = 51, p-value = 0.713Na podstawie przeprowadzonego testu Chowa należy odrzucić hipotezę zerową o stabilności parametrów modelu. Z kolei na podstawie testu CUSUM należy stwierdzić, że parametry modelu są stabilne.
10.4.5 Postać analityczna modelu
Aby zweryfikować hipotezę o poprawnym doborze postaci analitycznej modelu moż-
na skorzystać z testu RESET – lmtest::resettest. Możemy go przeprowadzić w kilku wersjach:
# wartości wyrównane podniesione do potęgi drugiej i trzeciej:
lmtest::resettest(m_dyn,power=2:3)##
## RESET test
##
## data: m_dyn
## RESET = 0.060498, df1 = 2, df2 = 50, p-value = 0.9414# wartości wyrównane podniesione do potęgi drugiej:
lmtest::resettest(m_dyn,power=2)##
## RESET test
##
## data: m_dyn
## RESET = 0.059816, df1 = 1, df2 = 51, p-value = 0.8078# wartości wyrównane podniesione do potęgi trzeciej:
lmtest::resettest(m_dyn,power=3)##
## RESET test
##
## data: m_dyn
## RESET = 0.096832, df1 = 1, df2 = 51, p-value = 0.7569Otrzymane wartości p-value wskazują, że brak jest podstaw do odrzucenia hipotezy zerowej zakładającej poprawną specyfikację modelu.