Rozdział 5 Analiza kanoniczna
Podstawowe problemy i wyniki analizy kanonicznej zostały sformułowane przez Harolda Hotellinga (wybitny ekonomista, matematyk, statystyk) w latach 1935-36. Powstała jako metoda do badania zależności pomiędzy dwoma zbiorami zmiennych. Do dziś doczekała się wielu uogólnień i rozszerzeń, np. na badanie relacji pomiędzy wieloma zbiorami zmiennych, na badane relacji w obecności współliniowych zmiennych (przez regularyzację) itp.
5.1 Problem
Mamy dwa zbiory zmiennych \(\{X_1,\dots,X_p\}\) i \(\{Y_1\dots,Y_p\}\).
Chcemy znaleźć taką kombinację liniową zmiennych z pierwszego zbioru, aby korelowała ona możliwie najsilniej ze zmiennymi z drugiego zbioru.
Innymi słowy, szukamy wektorów współczynników \(a\) i \(b\), takich, że \[cor(a^{\prime}X,b^{\prime}Y)\] jest możliwie największa.
5.2 Rozwiązanie
Wektor współczynników a to wektor własny odpowiadający największej wartości własnej macierzy \[S^{-1}_{22}S_{21}S^{-1}_{11}S_{12}\] a wektor współczynników b to wektor własny odpowiadający największej wartości własnej macierzy \[S^{-1}_{11}S_{12}S^{-1}_{22}S_{21}\] Korelacja \(cor(a^{\prime}X,b^{\prime}Y)\) to wartość największa wartość własna z powyższych macierzy.
[Wyprowadzenie na tablicy]
Nowe zmienne \(u_1=a^{\prime}X\) i \(v_1=b^{\prime}Y\) wyjaśniają największą część korelacji pomiędzy zbiorami wektorów \(X\) i \(Y\), ale nie całą.
Kolejnym krokiem jest znalezienie kolejnych zmiennych \(u_i=a_{i}X\) i \(u_i=b_iY\) , tak by:
wektory \(u_i\) są nieskorelowane pomiędzy sobą,
wektory \(v_i\) są nieskorelowane pomiędzy sobą,
korelacje \(cor(u_i,v_i)\) tworzą nierosnący ciąg odpowiadający możliwie największym cząstkowym korelacjom.
Jeżeli obserwacje pochodzą z wielowymiarowego modelu normalnego \(N(\mu,\sum)\) to możemy testować: \[H_0:R_i=0\forall_i\] Statystyka testowa dla testu ilorazu wiarogodności \[LRT=-n\sum_{i=k+1}^{s}\log(1-R^2_i)\] ma asymptotyczny rozkład \(\chi^2_{(p-k)(q-k)}\).
Wartość \(n\) w statystykach testowych zamienia się czasem na \(n - \frac{1}{2} (p + q + 3)\), co poprawia test.
5.3 Założenia
wielowymiarowa normalność,
brak obserwacji odstających (miara Cooka, Leverage, test Grubbsa, test Dixona)
brak współliniowości (reguła kciuka, wyznacznik \(>10^{-5}\) )
Liczba obserwacji powinna być większa od około 20*liczba zmiennych.
5.4 Jak to zrobić w R
Analiza kanoniczna jest zaimplementowana między innymi w pakiecie CCA w funkcji cc().
Prześledźmy poniższy kod
> library(CCA)
> dane = read.table("dane.csv",header=T,sep=";")
> X = dane[,c(9:10)]
# kolumny z waga
> Y = dane[,c(11:17)]
# kolumny z MDRD
> wynik = cc(X,Y)
> wynik$cor
[1] 0.3754946 0.1907164> wynik$xcoef
[,1]
[,2]
wagastart 0.1047822 -0.09276486
wagaend
-0.1154909 0.01404359
> wynik$ycoef
[,1]
[,2]
MDRD7
0.056059823 0.05799373
MDRD30 -0.059196976 -0.03981322
MDRD6m -0.006987328 0.02870234
MDRD12m -0.094082377 0.07732582
MDRD24m 0.119735985 -0.09688825
MDRD36m -0.024980200 -0.01744831
MDRD60m -0.007345604 0.04083270
> plot(wynik$cor,type="b")
> plt.cc(wynik,var.label=T)5.5 Przykładowe wyniki
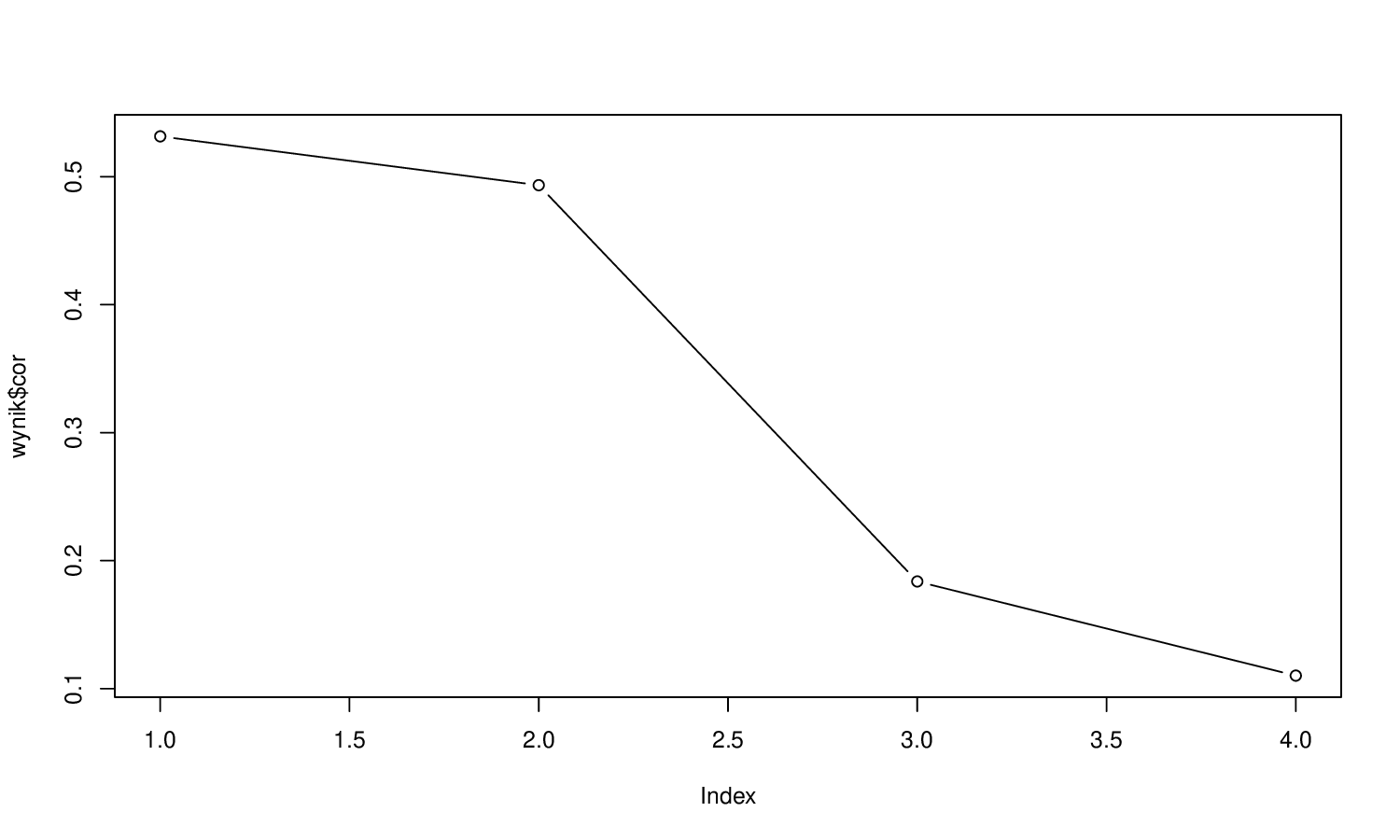
Rysunek 5.1: w1
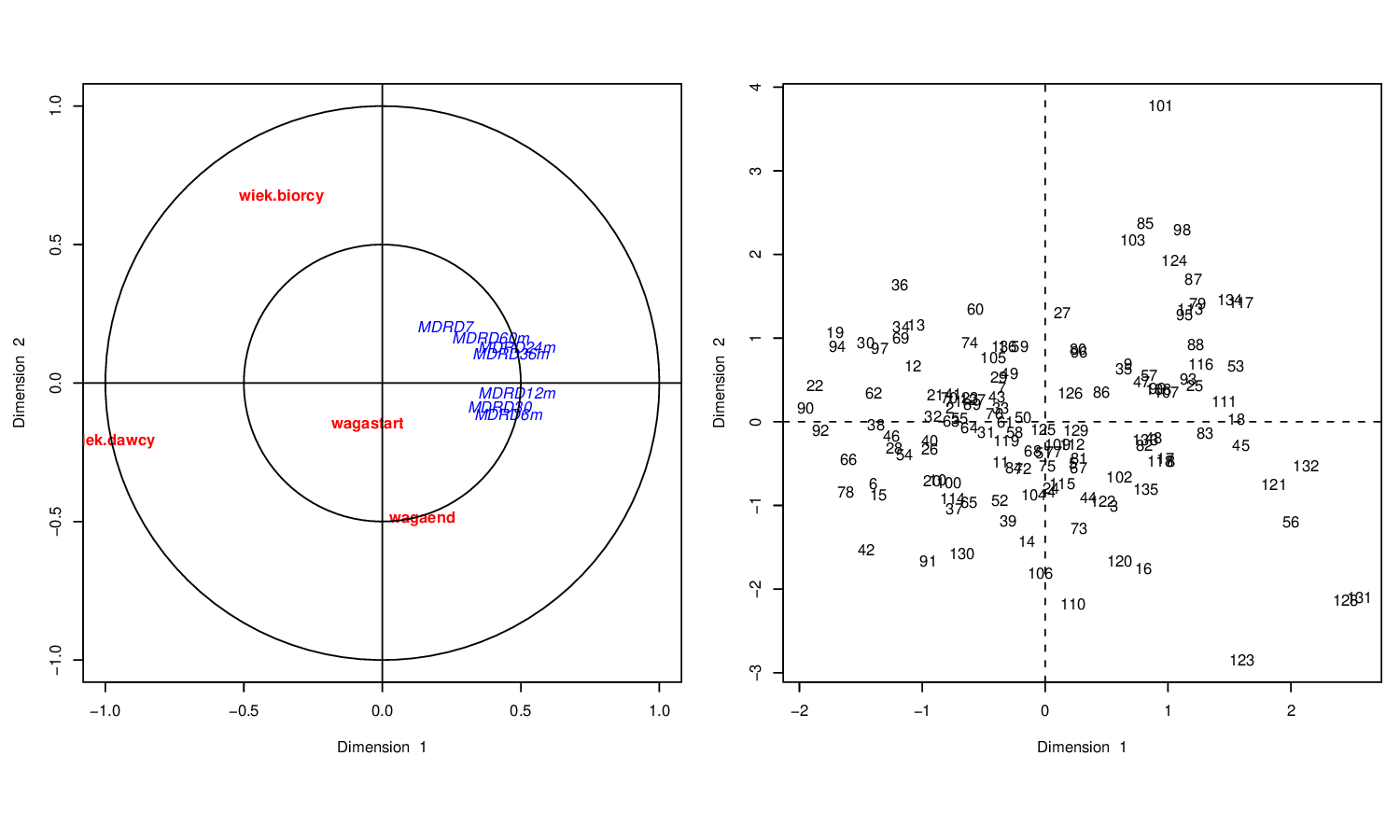
Rysunek 5.2: w2