Rozdział 6 Analiza korespondencji (odpowiedniości)
6.1 Problem
Obserwujemy dwie zmienne jakościowe. Pierwsza zmienna przyjmuje wartości z \(n_1\) poziomów, druga z \(n_2\) poziomów.
Interesuje nas, czy zmienne te są od siebie niezależne, a jeżeli nie są niezależne to które kombinacje poziomów występują ze sobą znacznie częściej. Dane z którymi mamy do czynienia to macierz kontyngencji (tabela wielodziel- cza) o wymiarach k × l wyznaczona dla dwóch zmiennych o odpowiednio \(k\) i \(l\) poziomach. Jeżeli \(k\) i \(l\) są małe, to taką macierz można ogarnąć rzutem oka. Jednak dla zmiennych występujących na wielu poziomach potrzebne są już dodatkowe narzędzia.
6.2 Rozwiązanie
Aby ocenić niezależność dwóch zmiennych można wykorzystać test \(\chi^2\) z funkcji
chisq.test() lub inny test dla macierzy kontyngencji (jeżeli poziomy są uporządkowane to dobrym rozwiązaniem będzie test Cochrana-Armitage). Testem tym zweryfikujemy hipotezę o niezależności częstości występowań poszczególnych zmiennych.
Jeżeli jednak odrzucimy tę hipotezę zerową, czyli przyjmiemy że jest JAKAŚ
zależność, to naturalnym pytaniem będzie jaka to zależność i pomiędzy którymi
poziomami.
Aby ocenić, które zmienne występują częściej ze sobą można wykonuje się tzw.
analizę korespondencji. Jeżeli zmienne były by niezależne od siebie, to zachodziło
by równanie
\[
p_{ij}=p_{i\cdot}p_{\cdot j},\quad i\in \{1\dots k\},\quad j\in \{1\dots l\}.
\]
gdzie \(p_{ij}\) to prawdopodobieństwo zaobserwowania pierwszej zmiennej na poziomie
\(i\) i jednocześnie drugiej na poziomie \(j\), \(p_{i\cdot}\) to prawdopodobieństwo zaobserwowania zmiennej pierwszej na poziomie \(i\) a \(p_{\cdot j}\) to prawdopodobieństwo zaobserwowania zmiennej drugiej na poziomie \(j\).
Żeby ocenić, które zmienne występują częściej lub rzadziej niż wynikało by to z niezależności, wyznaczymy standaryzowane reszty Pearsonowskie, zastąpimy też prawdopodobieństwa ich częstościowymi ocenami (czyli \(\hat{p}\) to liczba obserwowanych zdarzeń podzielona przez liczbę wszystkich obserwowanych zdarzeń) \[ \hat{e}_{ij}=\frac{\hat{p}_{ij}-\hat{p}_{i\cdot}\hat{p}_{\cdot j}}{\hat{p}_{i\cdot}\hat{p}_{\cdot j}} \] Duże dodatnie wartości \(\hat{e}_{ij}\) odpowiadają wysokiemu współwystępowaniu, ujemne \(E=[\hat{e}_{ij}]\) przedstawić w postaci graficznej używając tzw. biplotu. Innymi słowy wyznaczamy dekompozycję SVD macierzy E wartości odpowiadają występowaniu rzadszemu niż losowe. Możemy teraz macierz \[ E_{k\times l}=U_{k\times k}\sum_{k\times k}V_{l \times l}^{T} \]
Kolumny macierzy \(U_{k \times k}\) to wektory własne macierzy \(E^T E\) a kolumny macierzy \(V\) to wektory własne macierzy \(EE^T\). Na przekątnej macierzy diagonalnej \(\sigma\) znajdują się tzw. wartości singularne (osobliwe?) równe pierwiastkom z wartości własnych macierzy \(E^TE\) i EE^T . “Przy okazji”" kolumny macierzy \(U\) rozpinają ortonormalną bazę na kolumnach macierzy \(E\) a kolumny macierzy \(V\) rozpinają ortonormlaną bazę na wierszach macierzy \(E\). Można więc przedstawić macierz \(E\) (lub możliwie dużo informacji z tej macierzy) we nowej przestrzeni określonej na bazie współrzędnych wierszy i kolumn macierzy \(E\).
6.3 Jak to zrobić w R?
Przedstawimy funkcje ca(ca) oraz corresp(MASS). Obie służą do wykonania analizy
korespondencji. Wykonują ją jednak w odrobinę odmienny sposób przez co wyniki
końcowe też są inne.
6.4 Studium przypadku
Przedstawmy przykład bazujący na danych o zatrudnieniu w poszczególnych województwach. Zmienne które chcemy porównać to Województwo (16 poziomów) i Sektor pracy (4 poziomy: rolnictwo, przemysł, usługi, bezrobotni). Podejrzewamy, że struktura zatrudnienia różni się pomiędzy województwami.
library("MASS")
library("ca")
library("RColorBrewer")
# przygotujmy wektor kolorow
kolory = rev(brewer.pal(11,"Spectral"))
# wybierzmy interesujące nas kolumny
# konwertujemy tabele na macierz, takiego formatu spodziewa się funkcja heatmap()
dane = as.matrix(daneGUS[,c(22:25)])
colSums(dane)## pracujacy.rolnictwo pracujacy.przemysl pracujacy.uslugi
## 2249 4680 8309
## bezrobotni
## 743rowSums(dane)## DOLNOSLASKIE KUJAWSKO-POMORSKIE LODZKIE
## 1218 791 1304
## LUBELSKIE LUBUSKIE MALOPOLSKIE
## 1018 451 1336
## MAZOWIECKIE OPOLSKIE PODKARPACKIE
## 2373 379 852
## PODLASKIE POMORSKIE SLASKIE
## 478 792 1845
## SWIETOKRZYSKIE WARMINSKO-MAZURSKIE WIELKOPOLSKIE
## 622 573 1371
## ZACHODNIOPOMORSKIE
## 578# jak wygląda macierz z danymi?
head(dane)## pracujacy.rolnictwo pracujacy.przemysl pracujacy.uslugi
## DOLNOSLASKIE 74 415 651
## KUJAWSKO-POMORSKIE 128 245 369
## LODZKIE 220 384 636
## LUBELSKIE 328 197 447
## LUBUSKIE 43 151 244
## MALOPOLSKIE 205 381 689
## bezrobotni
## DOLNOSLASKIE 78
## KUJAWSKO-POMORSKIE 49
## LODZKIE 64
## LUBELSKIE 46
## LUBUSKIE 13
## MALOPOLSKIE 61Macierz 64 liczb jest trudno ogarnąć nieuzborojonym okiem. Możemy zauważyć, że biorąc pod uwagę, że najwięcej ludzi pracuje w sektorze usługowym (\(8309\) tys.) również łatwo zauważyć, że najludniejsze jest województwo Mazowieckie (\(2 373\) tys.) ale z tych surowych danych ciężko wyciągnąć głębszy wniosek.
# tę macierz można przedstawić w postaci graficznej
# czerwony odpowiada dużym liczbom, niebieski małym
heatmap(dane,scale="col",Colv=NA, col= kolory)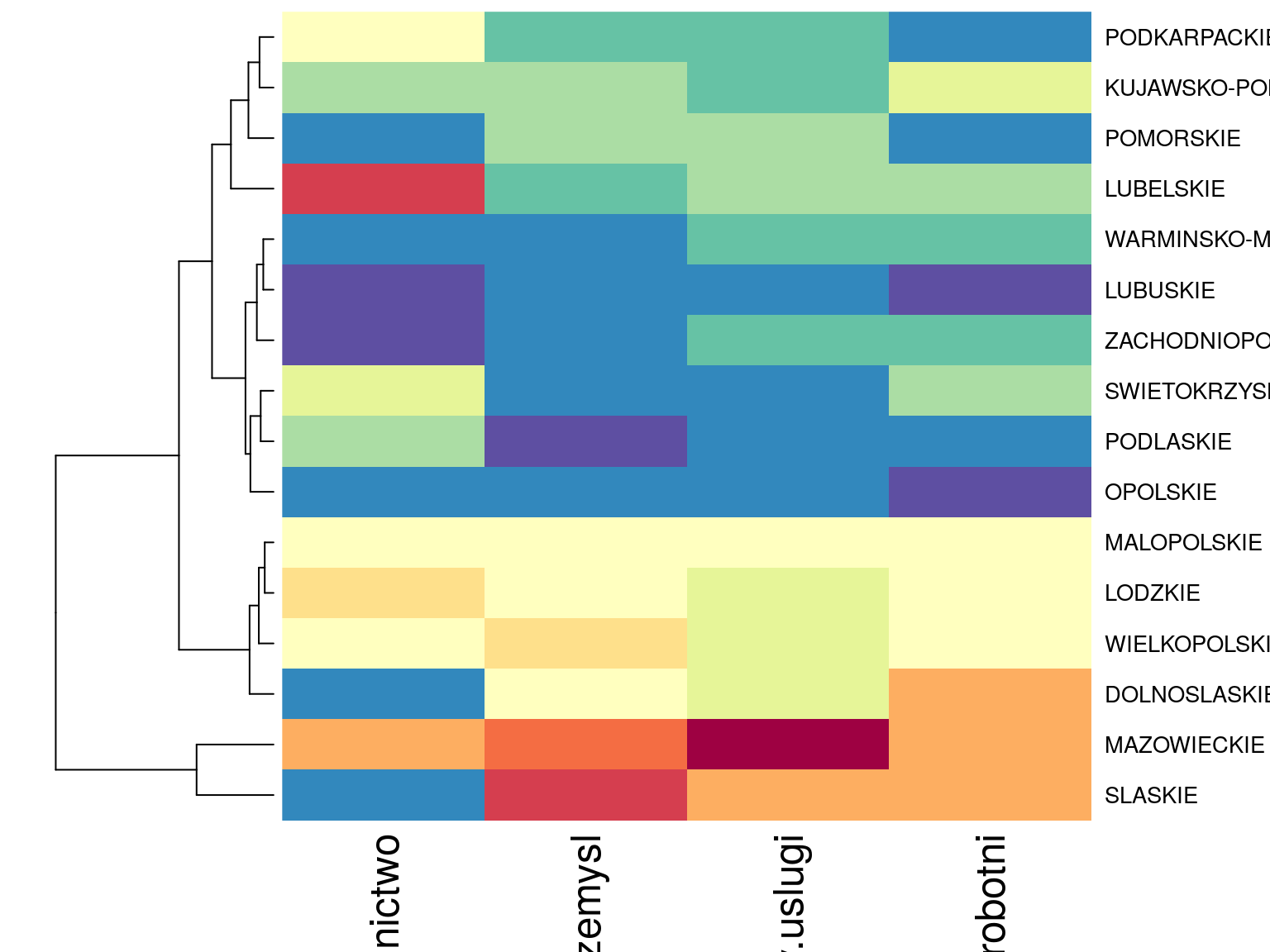
Rysunek 6.1: Mapa ciepła dla danych oryginalnych (kolory normalizowane po kolumnach).
# zobaczmy czy sa zaleznosci pomiedzy kolumnami i wierszami, wygląda na to że nie są to niezależne cechy
chisq.test(dane)##
## Pearson's Chi-squared test
##
## data: dane
## X-squared = 1031.9, df = 45, p-value < 2.2e-16Wykonaliśmy test \(\chi^2\) i otrzymaliśmy bardzo małą p-wartość, która upewniła nas w przekonaniu, że województwa mają inną strukturę zatrudnienia.
# zobaczmy które kombinacje występują częściej niż w przypadku niezależności
# policzymy residua Pearsonowskie
P = dane/sum(dane)
# macierz czestosci oczekiwanych
PP = outer(rowSums(P),colSums(P))
# macierz residuow Pearsonowskich
E = (P-PP)/sqrt(PP)
head(E)## pracujacy.rolnictwo pracujacy.przemysl pracujacy.uslugi
## DOLNOSLASKIE -0.058854443 0.024423457 0.005571820
## KUJAWSKO-POMORSKIE 0.012508000 0.006942431 -0.016485942
## LODZKIE 0.021307056 0.000860813 -0.012756112
## LUBELSKIE 0.122091621 -0.046327197 -0.028293827
## LUBUSKIE -0.020324264 0.013026864 0.004913504
## MALOPOLSKIE 0.009798815 -0.004097028 -0.001688693
## bezrobotni
## DOLNOSLASKIE 0.022465943
## KUJAWSKO-POMORSKIE 0.015945574
## LODZKIE 0.003427270
## LUBELSKIE -0.001528783
## LUBUSKIE -0.013765063
## MALOPOLSKIE -0.001118379# tę macierz również można przedstawić za pomocą mapy ciepła
heatmap(E,scale="none",Colv=NA,col= kolory)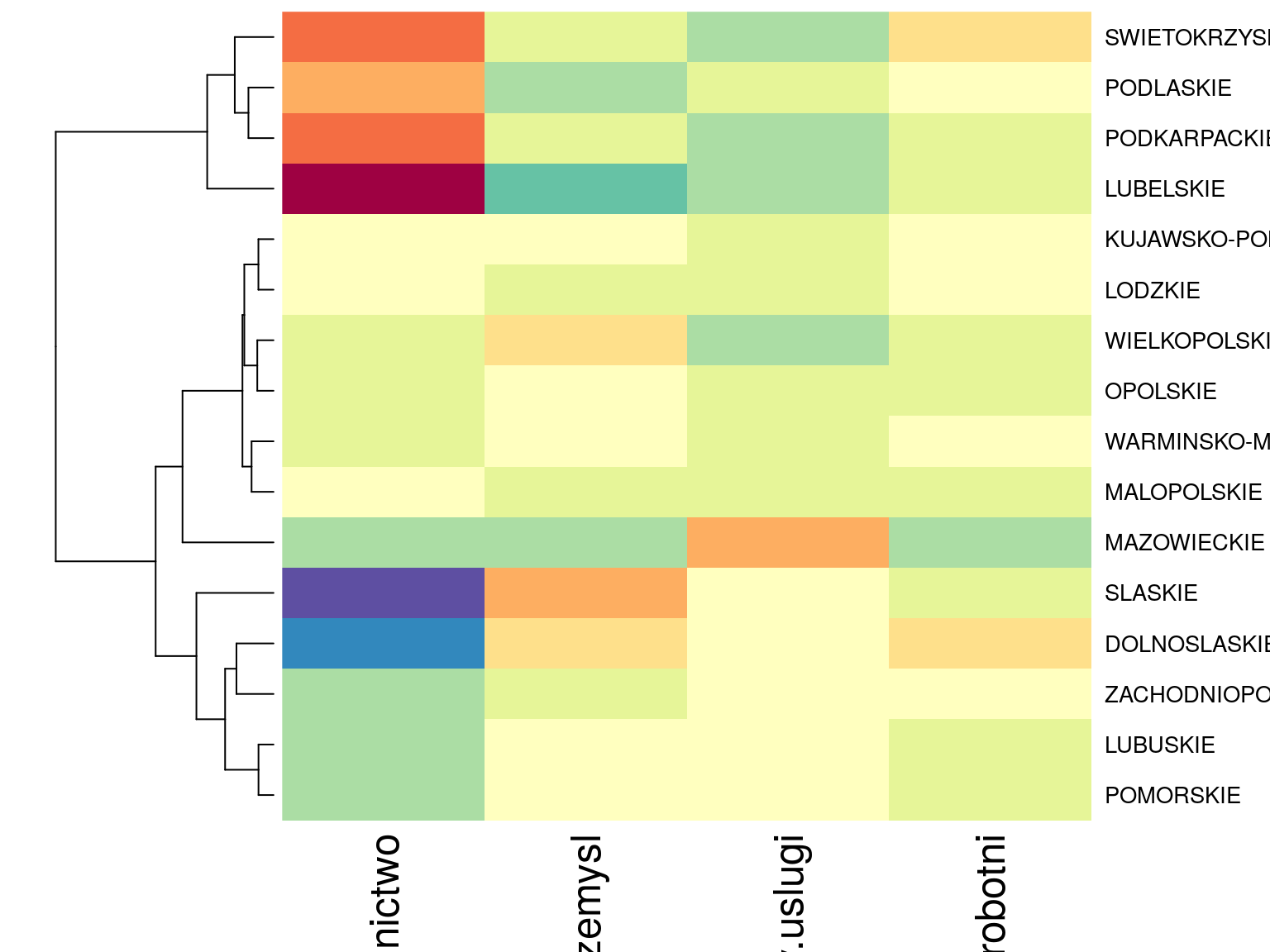
Rysunek 6.2: Mapa ciepła dla reszt Pearsonowskich.
Wyznaczyliśmy macierz reszt Pearsonowskich \(E\) (którą też przedstawiliśmy graficznie z użyciem mapy ciepła) i z tej macierzy możemy już odczytać w których województwach poszczególne sektory są popularniejsze. Największe reszty obserwujemy dla sektora rolnictwa, zarówno duże dodatnie wartości (w województwie lubelskim, podlaskim, podkarpackim i świętokrzyskim) jak i duże (co do modułu) ujemne wartości (w województwie śląskim i dolnośląskim). Możemy teraz przedstawić graficznie macierz \(E\) z użyciem biplotu (z wykorzystaniem dekompozycji SVD).
# wykonujemy dekompozycje na wartosci osobliwe (singularne/szczegolne)
A = svd(E)
X = t(apply(A$u, 1, "*", sqrt(A$d)))
Y = t(apply(A$v, 1, "*", sqrt(A$d)))
# zwykle współrzędne liczone są ze wzorow, w ktorych A jest dekompozycja innej macierzy
# [TODO: uzupełnić albo pominąć]
# A = Dr^(-1/2) A$u A$d
# B = Dc^(-1/2) A$v a$dplot(rbind(X[,1:2], Y[,1:2]), xlab="", ylab="", main="Bramka nr. 1", lwd
=3)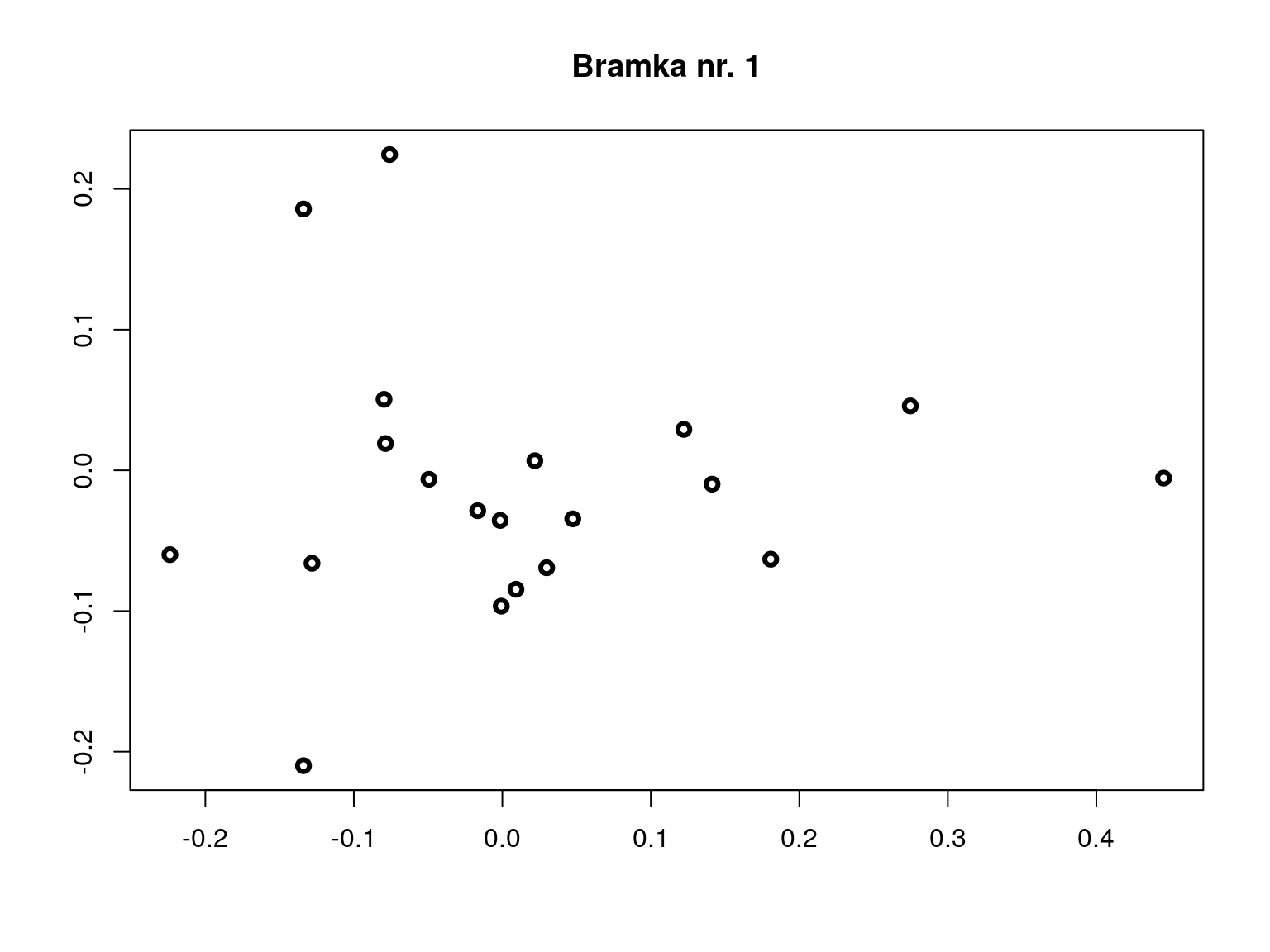
Rysunek 6.3: ?
# analiza korespondencji z użyciem pakietu MASS
biplot(MASS::corresp(dane, nf = 2))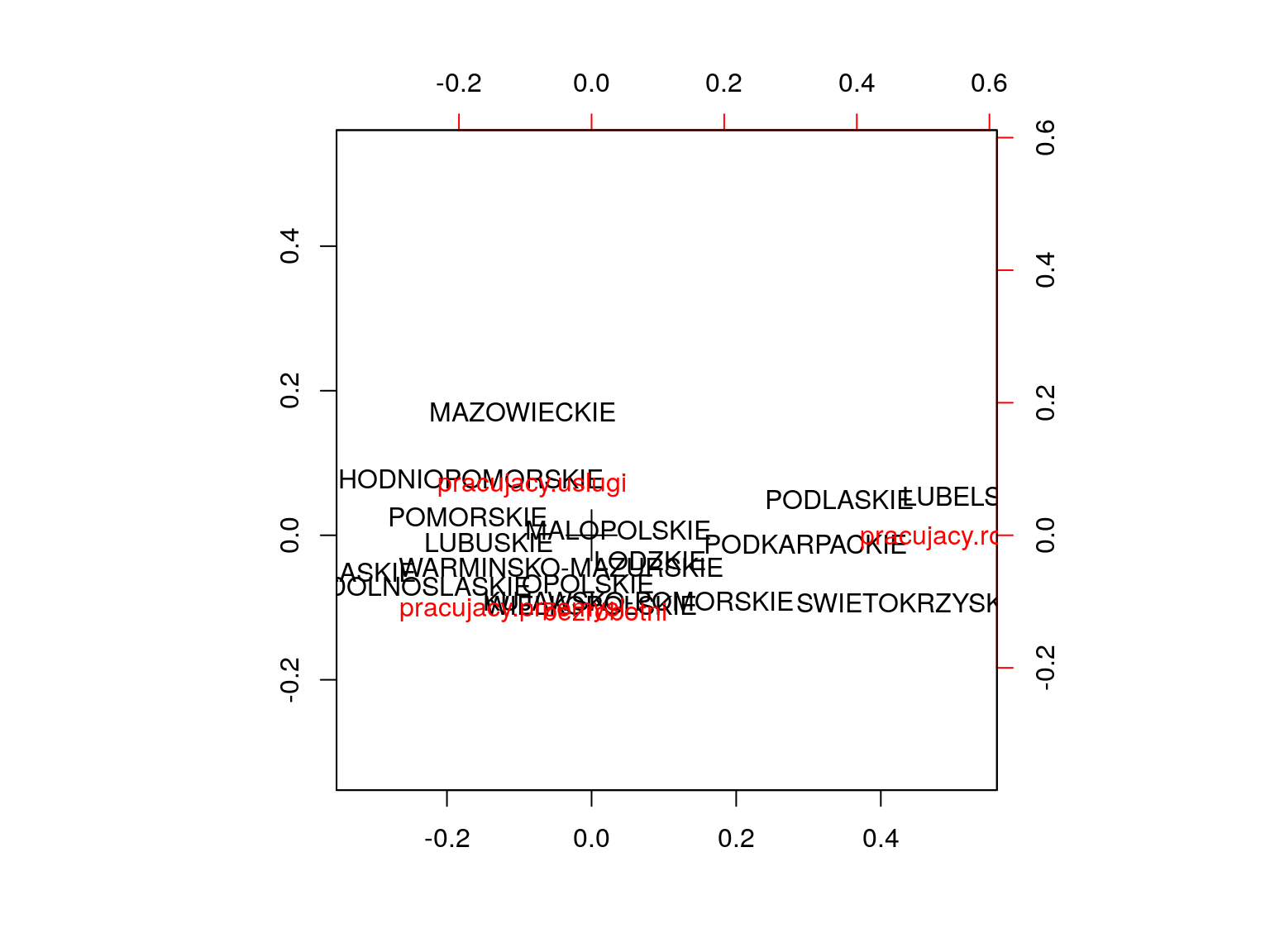
Rysunek 6.4: ?
# analiza korespondencji z użyciem pakietu ca
# argument mass powoduje że liczebności komórek odpowiadają wielkościom punktów na wykresie
plot(ca::ca(dane), mass=c(T,T))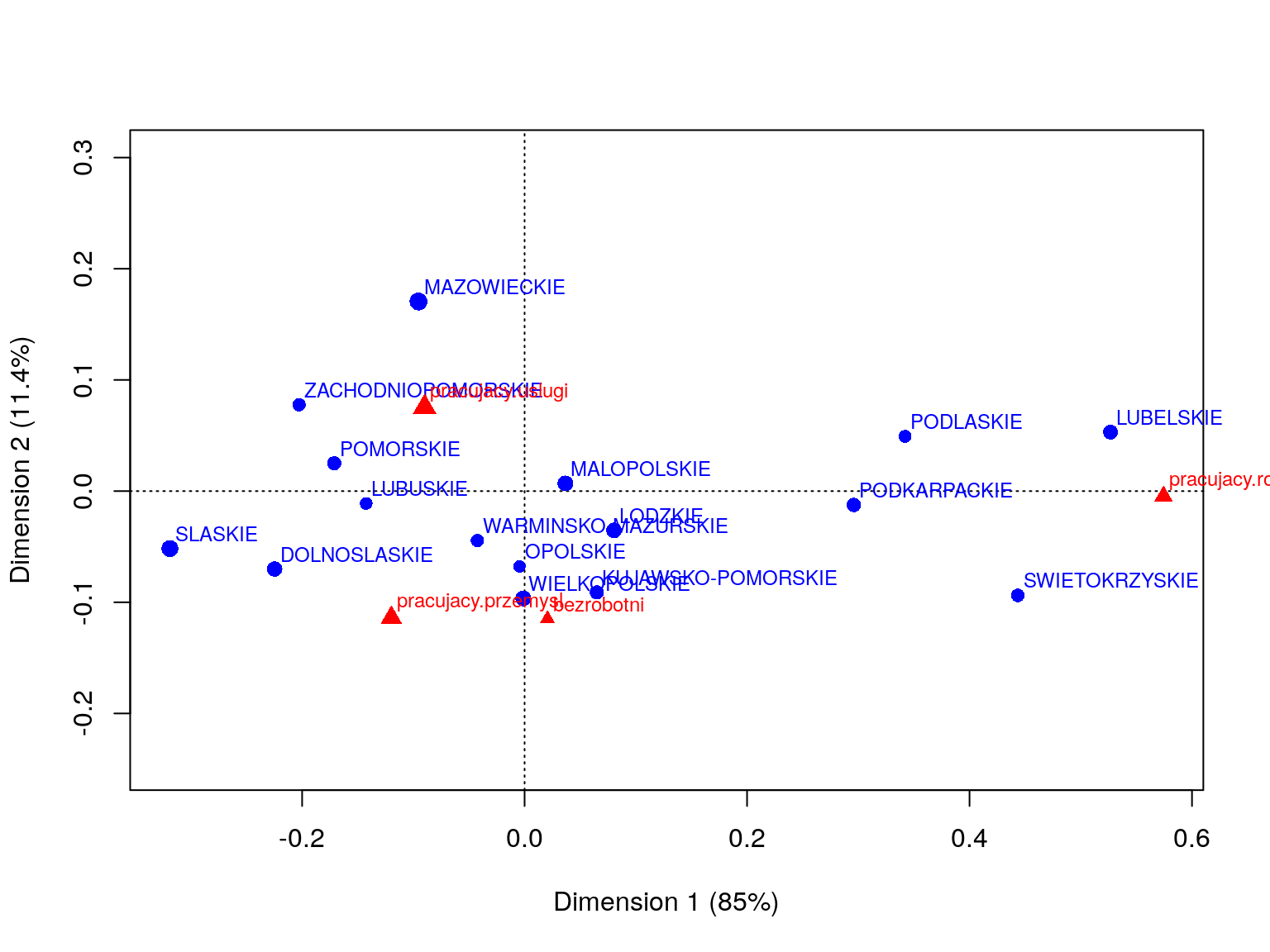
Rysunek 6.5: Przykład analizy korespondencji.
summary(ca::ca(dane))##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.054859 85.0 85.0 *********************
## 2 0.007352 11.4 96.3 ***
## 3 0.002360 3.7 100.0 *
## -------- -----
## Total: 0.064571 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | DOLN | 76 918 71 | -225 837 70 | -70 81 51 |
## 2 | KUJA | 49 848 11 | 65 286 4 | -91 563 56 |
## 3 | LODZ | 82 1000 10 | 80 838 10 | -35 162 14 |
## 4 | LUBE | 64 1000 277 | 527 990 322 | 53 10 24 |
## 5 | LUBU | 28 723 12 | -142 719 10 | -11 4 0 |
## 6 | MALO | 84 995 2 | 37 960 2 | 7 34 1 |
## 7 | MAZO | 148 1000 88 | -95 238 25 | 171 762 587 |
## 8 | OPOL | 24 496 3 | -5 2 0 | -68 494 15 |
## 9 | PODK | 53 926 78 | 296 925 85 | -12 2 1 |
## 10 | PODL | 30 994 56 | 342 974 64 | 49 20 10 |
## 11 | POMO | 50 939 24 | -171 919 26 | 25 20 4 |
## 12 | SLAS | 115 995 187 | -319 970 214 | -52 25 42 |
## 13 | SWIE | 39 968 128 | 443 926 139 | -94 41 47 |
## 14 | WARM | 36 515 4 | -42 246 1 | -44 269 10 |
## 15 | WIEL | 86 808 15 | -1 0 0 | -97 808 109 |
## 16 | ZACH | 36 806 33 | -203 702 27 | 78 103 30 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | prcjcyr | 141 999 720 | 574 999 847 | -4 0 0 |
## 2 | prcjcyp | 293 967 128 | -120 509 77 | -114 458 514 |
## 3 | prcjcys | 520 1000 111 | -90 587 77 | 75 413 402 |
## 4 | bzrb | 46 236 42 | 21 7 0 | -115 228 83 |Przy opisie analizy korespondencji często wymienianym czynnikiem jest inercja, nazywana czasem bezwładnością (przez podobieństwo do inercji w fizyce). Aby opisać formalnie czym jest ta miara musimy zacząć od kilku innych pojęć.
Niech masa wiersza i masa kolumny będzie określona jako brzegowe częstości macierzy kontyngencji.
(masa.kolumny = colSums(prop.table(dane)))## pracujacy.rolnictwo pracujacy.przemysl pracujacy.uslugi
## 0.14072962 0.29284776 0.51992992
## bezrobotni
## 0.04649271(masa.wiersza = rowSums(prop.table(dane)))## DOLNOSLASKIE KUJAWSKO-POMORSKIE LODZKIE
## 0.07621551 0.04949628 0.08159690
## LUBELSKIE LUBUSKIE MALOPOLSKIE
## 0.06370064 0.02822101 0.08359927
## MAZOWIECKIE OPOLSKIE PODKARPACKIE
## 0.14848883 0.02371566 0.05331331
## PODLASKIE POMORSKIE SLASKIE
## 0.02991052 0.04955885 0.11544960
## SWIETOKRZYSKIE WARMINSKO-MAZURSKIE WIELKOPOLSKIE
## 0.03892122 0.03585508 0.08578937
## ZACHODNIOPOMORSKIE
## 0.03616795Profilem wiersza (kolumny) będą wartości w wierszu (kolumnie) unormowane przez masę kolumny (wiersza).
head(profil.kolumny <- dane/rowSums(dane))## pracujacy.rolnictwo pracujacy.przemysl pracujacy.uslugi
## DOLNOSLASKIE 0.06075534 0.3407225 0.5344828
## KUJAWSKO-POMORSKIE 0.16182048 0.3097345 0.4664981
## LODZKIE 0.16871166 0.2944785 0.4877301
## LUBELSKIE 0.32220039 0.1935167 0.4390963
## LUBUSKIE 0.09534368 0.3348115 0.5410200
## MALOPOLSKIE 0.15344311 0.2851796 0.5157186
## bezrobotni
## DOLNOSLASKIE 0.06403941
## KUJAWSKO-POMORSKIE 0.06194690
## LODZKIE 0.04907975
## LUBELSKIE 0.04518664
## LUBUSKIE 0.02882483
## MALOPOLSKIE 0.04565868Tak unormowane profile wierszy i kolumn mogą być ze sobą porównywane. Im większa odległość pomiędzy profilami kolumn tym mniejsza zależność pomiędzy czynnikami opisanymi w tych kolumnach (oczywiście dla wierszy jest tak samo). Średni profil kolumnowy to masa wiersza a średni profil wierszowy to masa kolumn.
Inercja to odległość (w mierze \(\chi^2\) ) pomiędzy daną kolumną (wierszem, punktem) a średnią wartością dla kolumn (wierszy). Całkowita inercja to suma odległości dla wszystkich kolumn (wierszy). Im większa inercja tym punkty są oddalone dalej od średniego profilu wiersza/kolumny.
[TODO: uzupełnić. nawiązać do wyników funkcji summary.ca()]
Wyniki powyższych instrukcji oglądać można na wykresie 6.1 i kolejnych.
Analizując ten wykres można zauważyć ciekawe zróżnicowanie województw. Na
osi X największą współrzędną ma zmienna pr.rolnictwo, a więc to ta zmienna odpowiada największemu zróżnicowaniu województw. Wysoki wartości na tej osi osiągają województwa gdzie zatrudnienie w rolnictwie było wyższe niż średnie. Druga
oś rozróżnia województwa w których dominuje zatrudnienie w sektorze usług (dodatnie wartości) versus zatrudnieniu w przemyśle lub braku zatrudnienia (niestety
profil zatrudnienia w przemyśle i braku zatrudnienia jest podobny).
Osoby w województwach Mazowieckim i Zachodniopomorskim częściej pracują w sektorze usług, w województwach Lubelskim, Podlaskim, Świętokrzyskim i Podkarpackim dominuje zatrudnienie w sektorze rolniczym, w województwach Śląskim i Dolnośląskim dominuje zatrudnienie w przemyśle te województwa mają też większe problemy z bezrobociem.
[TODO: opisać podobieństwa i różnice do PCA]