Rozdział 8 Przykład analizy tabel wielodzielczych
8.1 Wprowadzenie
Zbiór danych, który zostanie wykorzystany do przeprowadzenia analiz jest dostępny
pod nazwą Titanic. Zawiera on informacje na temat losu 2201 pasażerów
oceanicznego liniowca “Titanic”. Do dyspozycji mamy cztery zmienne nominalne:
Class – klasy podróżowania: 1st (pierwsza), 2nd (druga), 3rd (trzecia), Crew (załoga),
Sex – płeć: Male (mężczyzna), Female (kobieta),
Age – wiek: Adult (dorosły), Child (dziecko),
Survived – przeżycie: No (nie), Yes (tak).
Oryginalny zestaw danych (wielowymiarowa tabela kontyngencji) został przekształcony o nazwie t. Fragment naszych
danych jest widoczny poniżej:
t <- DescTools::Untable(Titanic)
t[1:3,]## Class Sex Age Survived
## 1 3rd Male Child No
## 2 3rd Male Child No
## 3 3rd Male Child NoCelem naszych badań będzie próba opisu zależności między przeżyciem, a klasą podróżowania, płcią podróżnych oraz ich wiekiem.
8.2 Test chi-kwadrat
Do analizy zależności między dwiema zmiennymi zostanie wykorzystamy test \(\chi^2\). W
pakiecie R jest dostępna funkcja assocstats::vcd za pomocą której wykonywane
są dwa testy badające niezależność: test \(\chi^2\) oraz test \(G\):
gdzie:
\(r\) – liczba wierszy,
\(c\) – liczba kolumn,
\(O_{ij}\) – empiryczna liczebność \(i\)-tego wiersza oraz \(j\)-tej kolumny,
\(E_{ij}\) – oczekiwana liczebność \(i\)-tego wiersza oraz \(j\)-tej kolumny.
Dodatkowo podawane są również współczynniki korelacji: \(\phi\)-Yula, \(V\)-Pearsona i \(V\)-Cramera. A zatem spróbujmy odpowiedzieć na następujące pytania:
- Czy na przeżycie katastrofy miała wpływ płeć?
# tablica kontygencji:
s <- xtabs(~Survived+Sex, data=t)
gplots::balloonplot(s,dotcolor="gray80")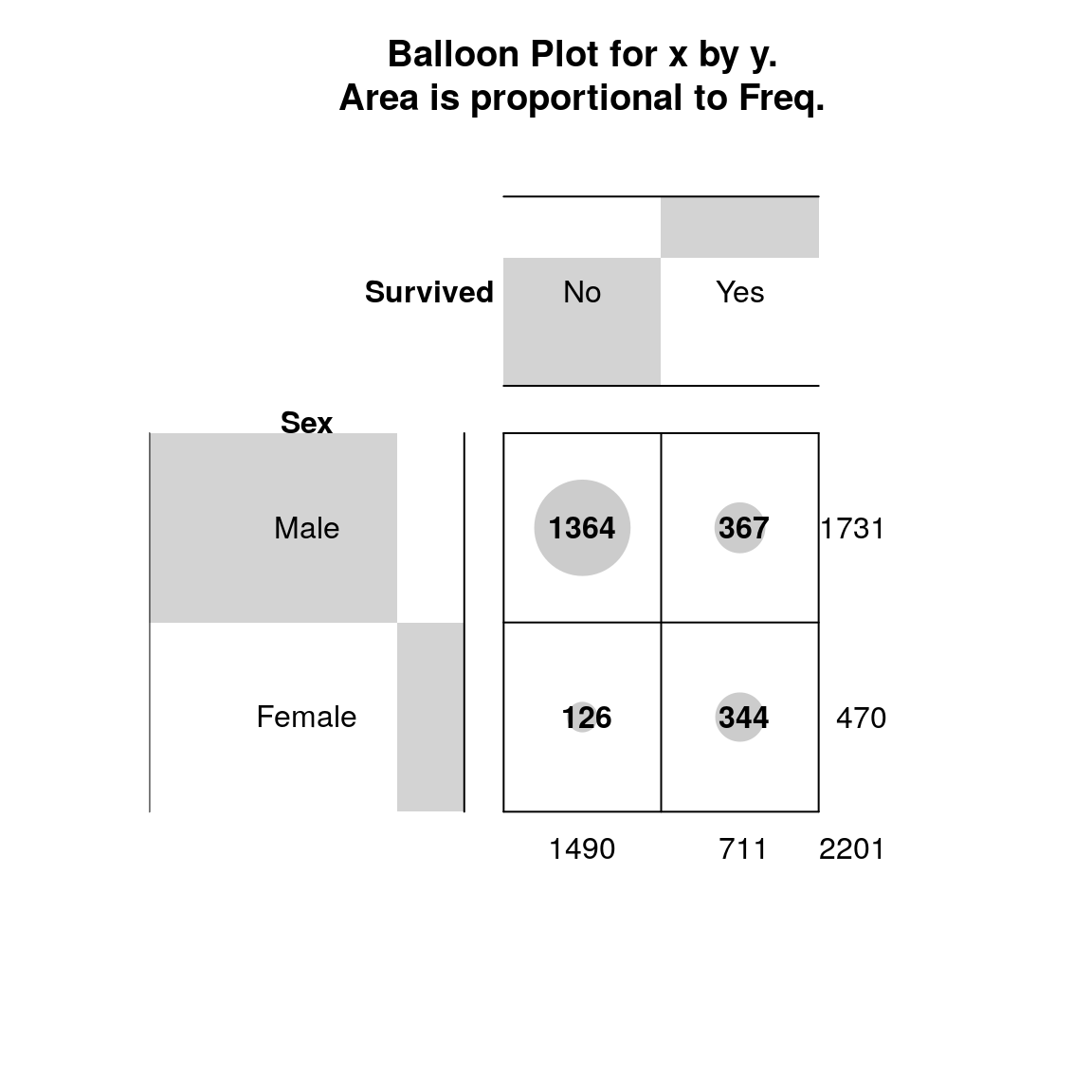
Rysunek 8.1: Przeżycie i płeć.
vcd::assocstats(s)## X^2 df P(> X^2)
## Likelihood Ratio 434.47 1 0
## Pearson 456.87 1 0
##
## Phi-Coefficient : 0.456
## Contingency Coeff.: 0.415
## Cramer's V : 0.456Na podstawie testu \(\chi^2\) oraz wykresu (rys. 8.1) możemy wnioskować, że występuje istotne powiązanie między przeżyciem katastrofy, a płcią pasażerów (p-value= 0, \(V = 0,456\)).
ps <- prop.table(s,2);ps## Sex
## Survived Male Female
## No 0.7879838 0.2680851
## Yes 0.2120162 0.7319149Obliczenia procentowe wskazują, że przeżyło \(73\%\) kobiet oraz tylko \(21\%\) mężczyzn.
ns<-ps/(1-ps);ns # szanse przeżycia## Sex
## Survived Male Female
## No 3.7166213 0.3662791
## Yes 0.2690616 2.7301587ns[,1]/ns[,2] # ilorazy szans przeżycia## No Yes
## 10.14696596 0.09855163Obliczony iloraz szans \(OR = 10,15\) wskazuje, że szansa przeżycia katastrofy na Titanicu wśród kobiet \((2,7301587)\) była ponad dziesięć razy większa niż wśród mężczyzn \((0,2690616)\).
- Czy na przeżycie katastrofy miała wpływ klasa w której podróżowano?
c <- xtabs(~Survived+Class,data=t) # tablica kontygencji
gplots::balloonplot(c,dotcolor="gray80")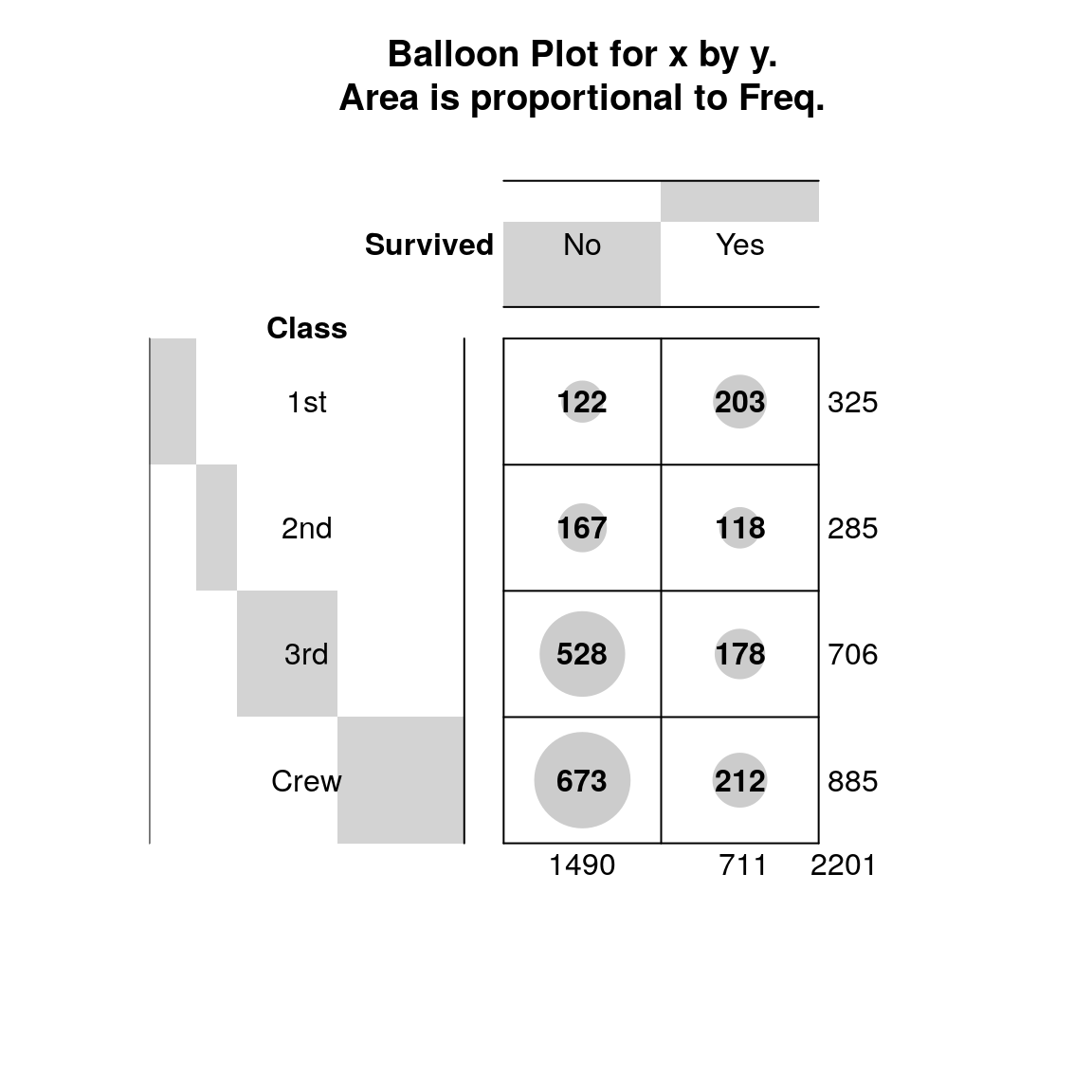
Rysunek 8.2: Przeżycie i klasa podróżowania.
vcd::assocstats(c)## X^2 df P(> X^2)
## Likelihood Ratio 180.9 3 0
## Pearson 190.4 3 0
##
## Phi-Coefficient : NA
## Contingency Coeff.: 0.282
## Cramer's V : 0.294Ponieważ p-value = 0 to należy sądzić, że istnieje zależność między przeżyciem a klasą w której podróżowali uczestnicy rejsu. O wysokim powiązaniu tych zmiennych świdczy także wysoki współczynnik korelacji \(V = 0,29\). Dodajmy, że współczynnik zależności \(\phi\) jest obliczany tylko dla tabel kontyngencji \(2\times2\).
pc <- prop.table(c,2);pc## Class
## Survived 1st 2nd 3rd Crew
## No 0.3753846 0.5859649 0.7478754 0.7604520
## Yes 0.6246154 0.4140351 0.2521246 0.2395480Po obliczeniu wartości procentowych dochodzimy do wniosku, że najwięcej przeżyło tych osób, które podróżowały w pierwszej klasie – \(62\%\). Natomiast wśród załogi przeżyło najmniej osób, tylko \(24\%\). Należy także podkreślić, że im wyższy standard podróży tym większa szansa przeżycia.
nc <- pc/(1-pc);nc # szanse przeżycia## Class
## Survived 1st 2nd 3rd Crew
## No 0.6009852 1.4152542 2.9662921 3.1745283
## Yes 1.6639344 0.7065868 0.3371212 0.3150074nc[,1]/nc[,2] # porównanie szans 1 z 2 klasą## No Yes
## 0.4246482 2.3548902nc[,2]/nc[,3] # porównanie szans 2 z 3 klasą## No Yes
## 0.4771122 2.0959429nc[,3]/nc[,4] # porównanie szans 3 z załogą## No Yes
## 0.9344041 1.0702008- Czy na przeżycie katastrofy miał wpływ wiek?
a <- xtabs(~Survived+Age,data=t) # tablica kontygencji
gplots::balloonplot(a,dotcolor="gray80")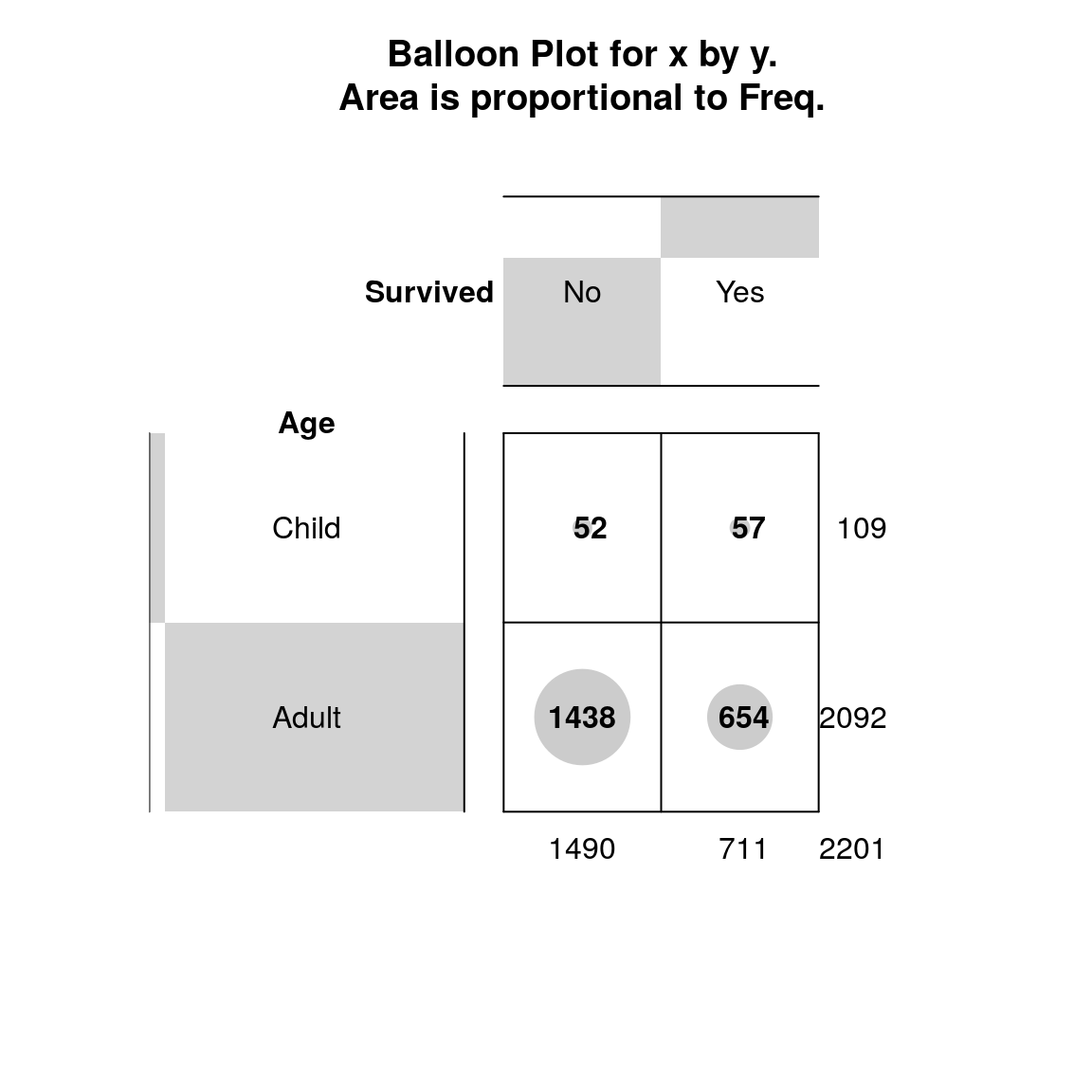
Rysunek 8.3: Przeżycie i wiek.
vcd::assocstats(a)## X^2 df P(> X^2)
## Likelihood Ratio 19.561 1 9.7458e-06
## Pearson 20.956 1 4.7008e-06
##
## Phi-Coefficient : 0.098
## Contingency Coeff.: 0.097
## Cramer's V : 0.098Także i w tym przypadku istnieje zależność między zmiennymi przeżycie oraz wiek, choć współczynnik korelacji nie jest zbyt wysoki i wynosi \(V = 0,098\).
pa <- prop.table(a,2);pa## Age
## Survived Child Adult
## No 0.4770642 0.6873805
## Yes 0.5229358 0.3126195Po obliczeniu wartości procentowych należy stwierdzić, że katastrofę przeżyła ponad połowa dzieci \((52\%)\) oraz \(13\) osób dorosłych \((31\%)\).
8.3 Model logitowy
Model logitowy daje dużo większe możliwości analizy tabel wielodzielczych niż test
\(\chi^2\). Omawiane w poprzenim rozdziale testy niezależności są przeznaczone do badania
zależności dwóch zmiennych jakościowych. Natomiast za pomocą modelu logitowego
mamy możliwość analizy wielowymiarowych tabel kontyngencji. Jdnak warunek jaki
musi zostać spełniony jest taki, aby zmienna zależna była zmienną binarną. W programie R dostępna jest funkcja glm za pomocą której możemy estymować
parametry modelu logitowego.
# ustawienie punktów odniesienia: Male oraz Adult:
tt <- transform(t,Sex=relevel(Sex,ref="Male"),Age=relevel(Age,ref="Adult"))
logit1 <- glm(Survived~.,tt,family=binomial)
summary(logit1)##
## Call:
## glm(formula = Survived ~ ., family = binomial, data = tt)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0812 -0.7149 -0.6656 0.6858 2.1278
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.3762 0.1362 -2.763 0.00573 **
## Class2nd -1.0181 0.1960 -5.194 2.05e-07 ***
## Class3rd -1.7778 0.1716 -10.362 < 2e-16 ***
## ClassCrew -0.8577 0.1573 -5.451 5.00e-08 ***
## SexFemale 2.4201 0.1404 17.236 < 2e-16 ***
## AgeChild 1.0615 0.2440 4.350 1.36e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2769.5 on 2200 degrees of freedom
## Residual deviance: 2210.1 on 2195 degrees of freedom
## AIC: 2222.1
##
## Number of Fisher Scoring iterations: 4Ten model jest dobrze dopasowany do danych. Potwierdzają to poniższe testy:
# test logarytmu wiarygodności:
lmtest::lrtest(logit1)## Likelihood ratio test
##
## Model 1: Survived ~ Class + Sex + Age
## Model 2: Survived ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 6 -1105.0
## 2 1 -1384.7 -5 559.4 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# test reszt deviance:
anova(logit1,test="Chisq")## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: Survived
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 2200 2769.5
## Class 3 180.90 2197 2588.6 < 2.2e-16 ***
## Sex 1 359.64 2196 2228.9 < 2.2e-16 ***
## Age 1 18.85 2195 2210.1 1.413e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# adekwatność modelu:
1-pchisq(deviance(logit1),logit1$df.residual)## [1] 0.4063859# dyspersja:
sum(resid(logit1,type="pearson")^2)/df.residual(logit1)## [1] 1.023531W kolejnym kroku obliczymy ilorazy wiarygodności na podstawie oszacowanych parametrów modelu.
cbind(OR=exp(coef(logit1)))## OR
## (Intercept) 0.6864493
## Class2nd 0.3612825
## Class3rd 0.1690159
## ClassCrew 0.4241466
## SexFemale 11.2465380
## AgeChild 2.8908263Interpretacja jest następująca:
podróżowanie w drugiej klasie dało o \(64\%\) mniej szans na przeżycie niż w pierwszej klasie,
podróżowanie w trzeciej klasie dało o \(83\%\) mniej szans na przeżycie niż w pierwszej klasie,
załoga statku miała o \(58\%\) mniej szans na przeżycie niż w pierwszej klasie,
kobiety miały ponad \(11\) razy większe szanse na przeżycie od mężczyzn,
dzieci miały prawie \(2,9\) razy większe szanse na przeżycie od dorosłych.
Uogólnione modele liniowe dają także możliwość badania bardziej złożonych zależności między zmiennymi tzn. interakcji.
logit2=glm(Survived~.^2,tt,family=binomial) # interakcje rzędu 2.
logit3=glm(Survived~.^3,tt,family=binomial) # interakcje rzędu 2 i 3.Po estymacji kilku modeli, zawsze jesteśmy zainteresowani, który z nich wybrać. Takiego wyboru możemy dokonać np. na podstawie kryterium informacyjnego AIC.
AIC(logit1,logit2,logit3)## df AIC
## logit1 6 2222.061
## logit2 12 2121.495
## logit3 14 2125.495Zatem do dalszych analiz powinniśmy wybrać model logit2 (z podwójnymi interakcjami) ponieważ charakteryzuje się najmiejszą wartością AIC. Naszą decyzję
potwierdzają także inne statystyki np. badające adekwatność modelu:
1-pchisq(deviance(logit1),logit1$df.residual)## [1] 0.40638591-pchisq(deviance(logit2),logit2$df.residual)## [1] 0.91812991-pchisq(deviance(logit3),logit3$df.residual)## [1] 0.9134249oraz oceniające istotność poszczególnych interakcji:
anova(logit3,test="Chisq")## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: Survived
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 2200 2769.5
## Class 3 180.90 2197 2588.6 < 2.2e-16 ***
## Sex 1 359.64 2196 2228.9 < 2.2e-16 ***
## Age 1 18.85 2195 2210.1 1.413e-05 ***
## Class:Sex 3 66.67 2192 2143.4 2.206e-14 ***
## Class:Age 2 44.21 2190 2099.2 2.507e-10 ***
## Sex:Age 1 1.69 2189 2097.5 0.1942
## Class:Sex:Age 2 0.00 2187 2097.5 1.0000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Tak więc najlepszym modelem okazał się logit2.
summary(logit2)##
## Call:
## glm(formula = Survived ~ .^2, family = binomial, data = tt)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6771 -0.7099 -0.5952 0.2374 2.2293
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.72763 0.16130 -4.511 6.45e-06 ***
## Class2nd -1.67026 0.32240 -5.181 2.21e-07 ***
## Class3rd -0.91330 0.20478 -4.460 8.20e-06 ***
## ClassCrew -0.52215 0.18088 -2.887 0.00389 **
## SexFemale 4.28298 0.53213 8.049 8.36e-16 ***
## AgeChild 16.99213 920.38639 0.018 0.98527
## Class2nd:SexFemale -0.06801 0.67120 -0.101 0.91929
## Class3rd:SexFemale -2.79995 0.56875 -4.923 8.52e-07 ***
## ClassCrew:SexFemale -1.13608 0.82048 -1.385 0.16616
## Class2nd:AgeChild 0.84881 1005.81951 0.001 0.99933
## Class3rd:AgeChild -16.34159 920.38646 -0.018 0.98583
## ClassCrew:AgeChild NA NA NA NA
## SexFemale:AgeChild -0.68679 0.52541 -1.307 0.19116
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2769.5 on 2200 degrees of freedom
## Residual deviance: 2097.5 on 2189 degrees of freedom
## AIC: 2121.5
##
## Number of Fisher Scoring iterations: 15Teraz obliczymy ilorazy wiarygodności aby je zinterpretować. Wyniki zostały zaokrąglone do dwóch miejsc po przecinku za pomocą funkcji round.
cbind(OR=round(exp(coef(logit2)),2))## OR
## (Intercept) 0.48
## Class2nd 0.19
## Class3rd 0.40
## ClassCrew 0.59
## SexFemale 72.46
## AgeChild 23965569.64
## Class2nd:SexFemale 0.93
## Class3rd:SexFemale 0.06
## ClassCrew:SexFemale 0.32
## Class2nd:AgeChild 2.34
## Class3rd:AgeChild 0.00
## ClassCrew:AgeChild NA
## SexFemale:AgeChild 0.50szansa przeżycia osób, które podróżowały w drugiej klasie była o \(81\%\) mniejsza niż w pierwszej klasie,
szansa przeżycia osób, które podróżowały w trzeciej klasie była o \(60\%\) mniejsza niż w pierwszej klasie,
szansa przeżycia załogi statku była o \(41\%\) mniejsza niż w pierwszej klasie,
kobiety miały ponad \(72\) razy większe szanse na przeżycie od mężczyzn,
dzieci miały również dużo większe szanse na przeżycie od dorosłych,
szansa przeżycia kobiet, które podróżowały w trzeciej klasie była mniejsza o \(94\%\) niż w pierwszej klasie,
szansa przeżycia dzieci, które podróżowały w drugiej klasie była ponad \(2\) razy większa niż w pierwszej klasie.
Funkcja glm umożliwia także wybór odpowiednich zmiennych do modelu. Jeśli
np. chcielibyśmy oszacować model logit2 ale tylko z istotnymi statystycznie parametrami to kod wyglądałby następująco:
myl <- glm(Survived~Class+Sex+Age+I(Class=="3rd" & Sex=="Female"),tt,
family=binomial)
summary(myl)##
## Call:
## glm(formula = Survived ~ Class + Sex + Age + I(Class == "3rd" &
## Sex == "Female"), family = binomial, data = tt)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.5435 -0.7070 -0.5798 0.3842 2.0293
##
## Coefficients:
## Estimate Std. Error z value
## (Intercept) -0.6337 0.1506 -4.208
## Class2nd -1.2888 0.2385 -5.404
## Class3rd -1.0642 0.1935 -5.500
## ClassCrew -0.6252 0.1708 -3.661
## SexFemale 3.8283 0.2715 14.098
## AgeChild 1.0522 0.2306 4.563
## I(Class == "3rd" & Sex == "Female")TRUE -2.4578 0.3302 -7.443
## Pr(>|z|)
## (Intercept) 2.57e-05 ***
## Class2nd 6.52e-08 ***
## Class3rd 3.80e-08 ***
## ClassCrew 0.000252 ***
## SexFemale < 2e-16 ***
## AgeChild 5.05e-06 ***
## I(Class == "3rd" & Sex == "Female")TRUE 9.81e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2769.5 on 2200 degrees of freedom
## Residual deviance: 2145.1 on 2194 degrees of freedom
## AIC: 2159.1
##
## Number of Fisher Scoring iterations: 58.4 Model logitowy
Innym sposobem analizy wielowymiarowych tabel kontyngencji jest zastosowanie modelu Poissona. Procedura estymacji i diagnostyki przebiega w taki sam sposób jak w przypadku modelu logitowego. Należy jednak pamiętać o tym, że w tego typu modelach zmienna zależna ma rozkład Poissona. A zatem nasz zbiór danych należy przekształcić.
f <- as.data.frame(xtabs(~Survived+Class+Sex+Age,tt))
f[1:3,]## Survived Class Sex Age Freq
## 1 No 1st Male Adult 118
## 2 Yes 1st Male Adult 57
## 3 No 2nd Male Adult 154p1 <- glm(Freq~.,f,family=poisson)
p2 <- glm(Freq~.^2,f,family=poisson)
p3 <- glm(Freq~.^3,f,family=poisson)
p4 <- glm(Freq~.^4,f,family=poisson)
# kryteria informacyjne:
AIC(p1,p2,p3,p4)## df AIC
## p1 7 1385.0654
## p2 19 281.9902
## p3 29 185.4021
## p4 32 191.4021# adekwatność modelu:
1-pchisq(deviance(p1),p1$df.residual)## [1] 01-pchisq(deviance(p2),p2$df.residual)## [1] 01-pchisq(deviance(p3),p3$df.residual)## [1] 11-pchisq(deviance(p4),p4$df.residual)## [1] 0# istotność poszczególnych interakcji:
anova(p4,test="Chisq")## Analysis of Deviance Table
##
## Model: poisson, link: log
##
## Response: Freq
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 31 4953.1
## Survived 1 281.78 30 4671.4 < 2.2e-16 ***
## Class 3 475.81 27 4195.5 < 2.2e-16 ***
## Sex 1 768.32 26 3427.2 < 2.2e-16 ***
## Age 1 2183.56 25 1243.7 < 2.2e-16 ***
## Survived:Class 3 180.90 22 1062.8 < 2.2e-16 ***
## Survived:Sex 1 434.47 21 628.3 < 2.2e-16 ***
## Survived:Age 1 19.56 20 608.7 9.746e-06 ***
## Class:Sex 3 337.77 17 271.0 < 2.2e-16 ***
## Class:Age 3 154.35 14 116.6 < 2.2e-16 ***
## Sex:Age 1 0.02 13 116.6 0.8882240
## Survived:Class:Sex 3 65.30 10 51.3 4.336e-14 ***
## Survived:Class:Age 3 29.34 7 22.0 1.900e-06 ***
## Survived:Sex:Age 1 12.17 6 9.8 0.0004857 ***
## Class:Sex:Age 3 9.78 3 0.0 0.0205004 *
## Survived:Class:Sex:Age 3 0.00 0 0.0 1.0000000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# ilorazy wiarygodności:
cbind(OR=round(exp(coef(p3)),1))## OR
## (Intercept) 1.180000e+02
## SurvivedYes 5.000000e-01
## Class2nd 1.300000e+00
## Class3rd 3.300000e+00
## ClassCrew 5.700000e+00
## SexFemale 0.000000e+00
## AgeChild 0.000000e+00
## SurvivedYes:Class2nd 2.000000e-01
## SurvivedYes:Class3rd 4.000000e-01
## SurvivedYes:ClassCrew 6.000000e-01
## SurvivedYes:SexFemale 7.250000e+01
## SurvivedYes:AgeChild 9.354350e+10
## Class2nd:SexFemale 2.500000e+00
## Class3rd:SexFemale 6.800000e+00
## ClassCrew:SexFemale 1.000000e-01
## Class2nd:AgeChild 4.000000e-01
## Class3rd:AgeChild 9.644408e+10
## ClassCrew:AgeChild 0.000000e+00
## SexFemale:AgeChild 2.000000e-01
## SurvivedYes:Class2nd:SexFemale 9.000000e-01
## SurvivedYes:Class3rd:SexFemale 1.000000e-01
## SurvivedYes:ClassCrew:SexFemale 3.000000e-01
## SurvivedYes:Class2nd:AgeChild 2.550000e+01
## SurvivedYes:Class3rd:AgeChild 0.000000e+00
## SurvivedYes:ClassCrew:AgeChild 0.000000e+00
## SurvivedYes:SexFemale:AgeChild 5.000000e-01
## Class2nd:SexFemale:AgeChild 2.500000e+00
## Class3rd:SexFemale:AgeChild 1.310000e+01
## ClassCrew:SexFemale:AgeChild 4.034000e+02Na podstawie otrzymanych ilorazów wiarygodności możemy również sformułować kilka wniosków:
szanse zgonu w poszczególnych klasach były większe niż w pierwszej klasie o: \(30\%\) w klasie drugiej, ponad 3 razy większe w klasie trzeciej oraz prawie sześciokrotnie większe wśród załogi.
szanse przeżycia w poszczególnych klasach były mniejsze niż w pierwszej klasie o: \(80\%\) w klasie drugiej, \(60\%\) w klasie trzeciej i \(40\%\) wśród załogi. Z kolei szansa przeżycia kobiet była ponad \(72\) razy większa niż mężczyzn, także dzieci miały wielokrotnie większe szanse na przeżycie niż dorośli.
szanse przeżycia w poszczególnych klasach wśród kobiet były mniejsze niż dla kobiet podróżujących w pierwszej klasie o: \(10\%\) w klasie drugiej, \(90\%\) w klasie trzeciej i \(70\%\) wśród żeńskiej załogi statku.
W środowisku R dostępne są także inne funkcje za pomocą których możemy ana-
lizować wielowymiarowe tabele wielodzielcze np. MASS::loglm lub loglin.