Rozdział 11 Przegląd wybranych testów statystycznych
11.1 Testy normalności
W celu przedstawienia procedury obliczeniowej testu normalności Doornika-Hansena wykorzystamy dane dotyczące długości płatka kosaćca z gatunku setosa.
attach(iris)
f <- Petal.Length[Species=="setosa"]Przed przystąpieniem do obliczeń statystyki jednowymiarowego testu normalności Doornika-Hansena, należy przekształcić nasz wektor danych f w następujący sposób:
ff <- f-mean(f) # przekształcenie
n <- length(ff) # liczebność wektora danychTeraz dokonamy transformacji skośności (D’Agostino) czyli obliczymy statystykę z1:
\[\begin{equation} \beta=\frac{3(n^2+27n-70)(n+1)(n+3)}{(n-2)(n+5)(n+7)(n+9)} \tag{11.1} \end{equation}\]
\[\begin{equation} \omega^2=-1+\left[2(\beta-1)\right]^{1/2} \tag{11.2} \end{equation}\]
\[\begin{equation} \delta=\left[\ln\left(\sqrt{\omega^2}\right)\right]^{-1/2} \tag{11.3} \end{equation}\]
\[\begin{equation} S_1=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{\sqrt{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^3}} \tag{11.4} \end{equation}\]
\[\begin{equation} y=S_1\left[\frac{\omega^2-1}{2}\frac{(n+1)(n+3)}{6(n-2)}\right]^{1/2} \tag{11.5} \end{equation}\]
\[\begin{equation} z_1=\delta\ln\left[y+(y^2+1)^{1/2}\right] \tag{11.6} \end{equation}\]
# obliczenia dla z1:
f1 <- function(x){
DNAME= deparse(substitute(x))
x= sort(x[complete.cases(x)])
n= length(x)
beta= (3*(n^2+27*n-70)*(n+1)*(n+3)) / ((n-2)*(n+5)*(n+7)*(n+9))
w2= -1+(2*(beta-1))^(1/2)
del= 1/sqrt(log(sqrt(w2)))
S1= e1071::skewness(x,type=1) # parametr skośności
y= S1*sqrt(((w2-1) / (2))*(((n+1)*(n+3))/(6*(n-2))))
z1= del*log(y+sqrt(y^2+1))
}
z1 <- f1(ff); z1## [1] 0.3315036Należy zaznaczyć, że statystyka z1 ma rozkład zbliżony do rozkładu normalnego.
# rozkład statystyki z1 dla 10000 replikacji
statsS <- sapply(1:10000, function(i) f1(sample(ff,length(ff),TRUE)))par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(statsS,prob=TRUE,col='SteelBlue',border='white')
curve(dnorm(x,mean(statsS),sd(statsS)),add=TRUE,lwd=3,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))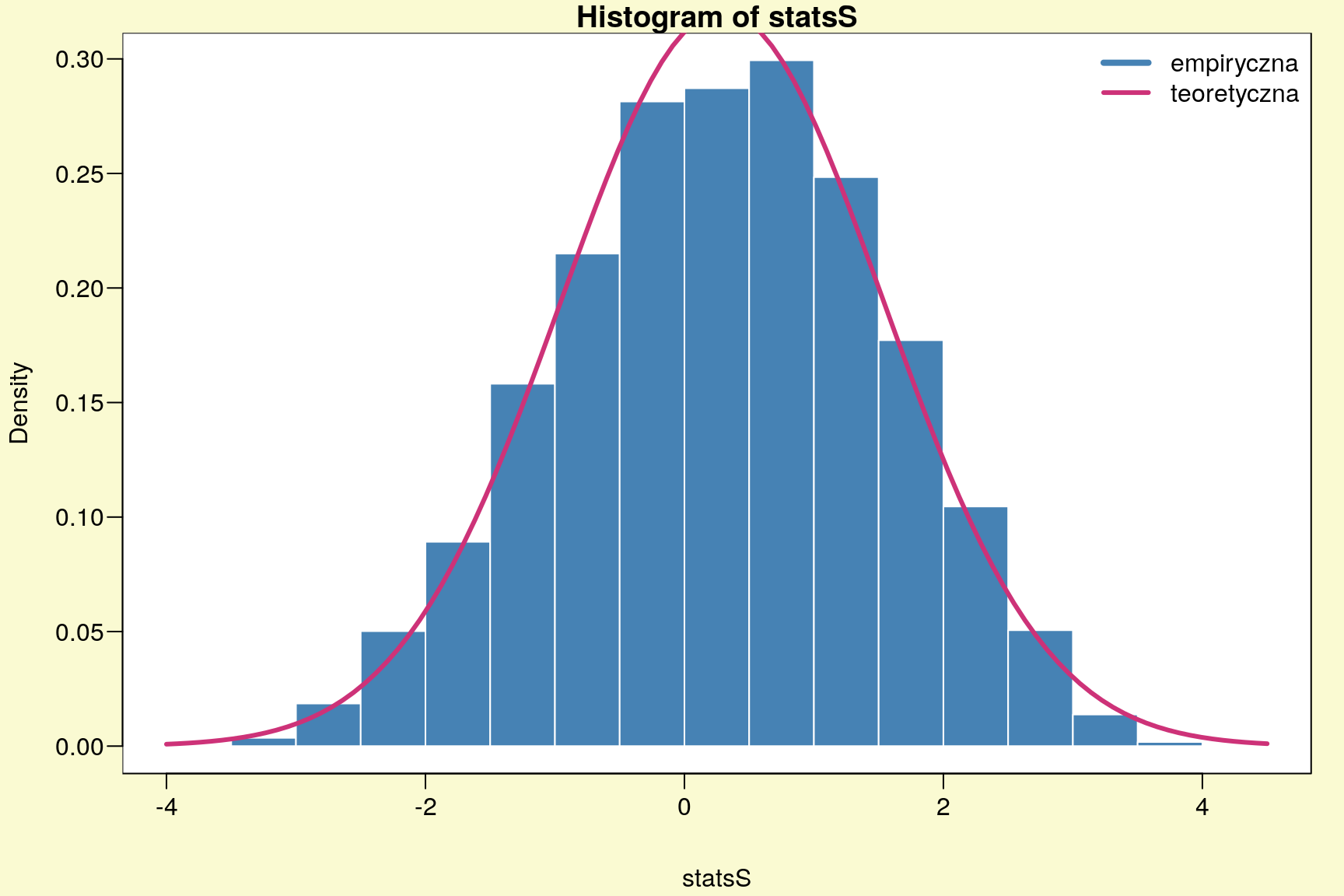
Rysunek 11.1: Rozkład statystyki z1 dla 10000 replikacji.
Otrzymaną wartość z1 możemy wykorzystać do zweryfikowania następujących hipotez dotyczących skośności (wzór (11.4)):
\[
\begin{array}{ll}
H_0: & S_1 = 0\\
H_1: & S_1 \neq 0
\end{array}
\qquad\text{lub}\qquad
\begin{array}{ll}
H_0: & S_1 \geq 0\\
H_1: & S_1 < 0
\end{array}
\qquad\text{lub}\qquad
\begin{array}{ll}
H_0: & S_1 \leq 0\\
H_1: & S_1 > 0
\end{array}
\]
2*(1-pnorm(abs(z1))) # p-value dla H1: S1!=0## [1] 0.7402641pnorm(z1) # p-value dla H1: S1<0## [1] 0.62986791-pnorm(z1) # p-value dla H1: S1>0## [1] 0.3701321Do weryfikacji tego typu hipotez możemy skorzystać z testu skośności D’Agostino wpisując następującą komendę:
moments::agostino.test(f)##
## D'Agostino skewness test
##
## data: f
## skew = 0.10318, z = 0.33150, p-value = 0.7403
## alternative hypothesis: data have a skewnessJak można zauważyć wartość statystyki z jest taka sama jak z1. Warto dodać, że we wzorach (11.3) oraz (11.6) może być stosowany
logarytm dziesiętny – \(\log\) zamiast logarytu naturalnego – \(\ln\). Wtedy wyniki
testów D’Agostino mogą się różnić.
W kolejnym kroku obliczymy statystykę z2 czyli przeprowadzimy transformację
kurtozy (Wilson-Hilferty) według poniższych wzorów:
\[\begin{equation}
\delta= (n-3)(n+1)(n^2+15n-4)
\tag{11.7}
\end{equation}\]
\[\begin{equation} a=\frac{(n-2)(n+5)(n+7)(n^2+27n-70)}{6\;\delta} \tag{11.8} \end{equation}\]
\[\begin{equation} c=\frac{(n-7)(n+5)(n+7)(n^2+2n-5)}{6\;\delta} \tag{11.9} \end{equation}\]
\[\begin{equation} k=\frac{(n+5)(n+7)(n^3+37n^2+11n-313)}{12\;\delta} \tag{11.10} \end{equation}\]
\[\begin{equation} S_1=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{\sqrt{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^3}} \tag{11.11} \end{equation}\]
\[\begin{equation} \alpha=a+{S_1}^2c \tag{11.12} \end{equation}\]
\[\begin{equation} K_1=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^2} \tag{11.13} \end{equation}\]
\[\begin{equation} \chi=(K_1-1-{S_1}^2)2k \tag{11.14} \end{equation}\]
\[\begin{equation} z_2=\left[\left(\frac{\chi}{2\alpha}\right)^{1/3}-1+\frac{1}{9\alpha}\right](9\alpha)^{1/2} \tag{11.15} \end{equation}\]
# obliczenia dla z2:
f2 <- function(x){
DNAME= deparse(substitute(x))
x= sort(x[complete.cases(x)])
n= length(x)
delta= (n-3)*(n+1)*(n^2+15*n-4)
a= ((n-2)*(n+5)*(n+7)*(n^2+27*n-70)) / (6*delta)
c= ((n-7)*(n+5)*(n+7)*(n^2+2*n-5)) / (6*delta)
k= ((n+5)*(n+7)*(n^3+37*n^2+11*n-313)) / (12*delta)
S1= e1071::skewness(x,type=1) # parametr skośności
alpha= a+S1^2*c
K1= e1071::kurtosis(x,type=1)+3 # parametr kurtozy
chi= (K1-1-S1^2)*2*k
z2= ( (chi/(2*alpha))^(1/3)-1+(1/(9*alpha)) )*sqrt(9*alpha)
}
z2 <- f2(ff); z2## [1] 2.04261Także parametr z2 ma rozkład zbliżony do rozkładu normalnego (rys. 11.2).
# rozkład statystyki z2 dla 10000 replikacji
statsK <- sapply(1:10000, function(i) f2(sample(ff,length(ff),TRUE)))par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(statsK,prob=TRUE,col='SteelBlue',border='white')
curve(dnorm(x,mean(statsK),sd(statsK)),add=TRUE,lwd=3,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))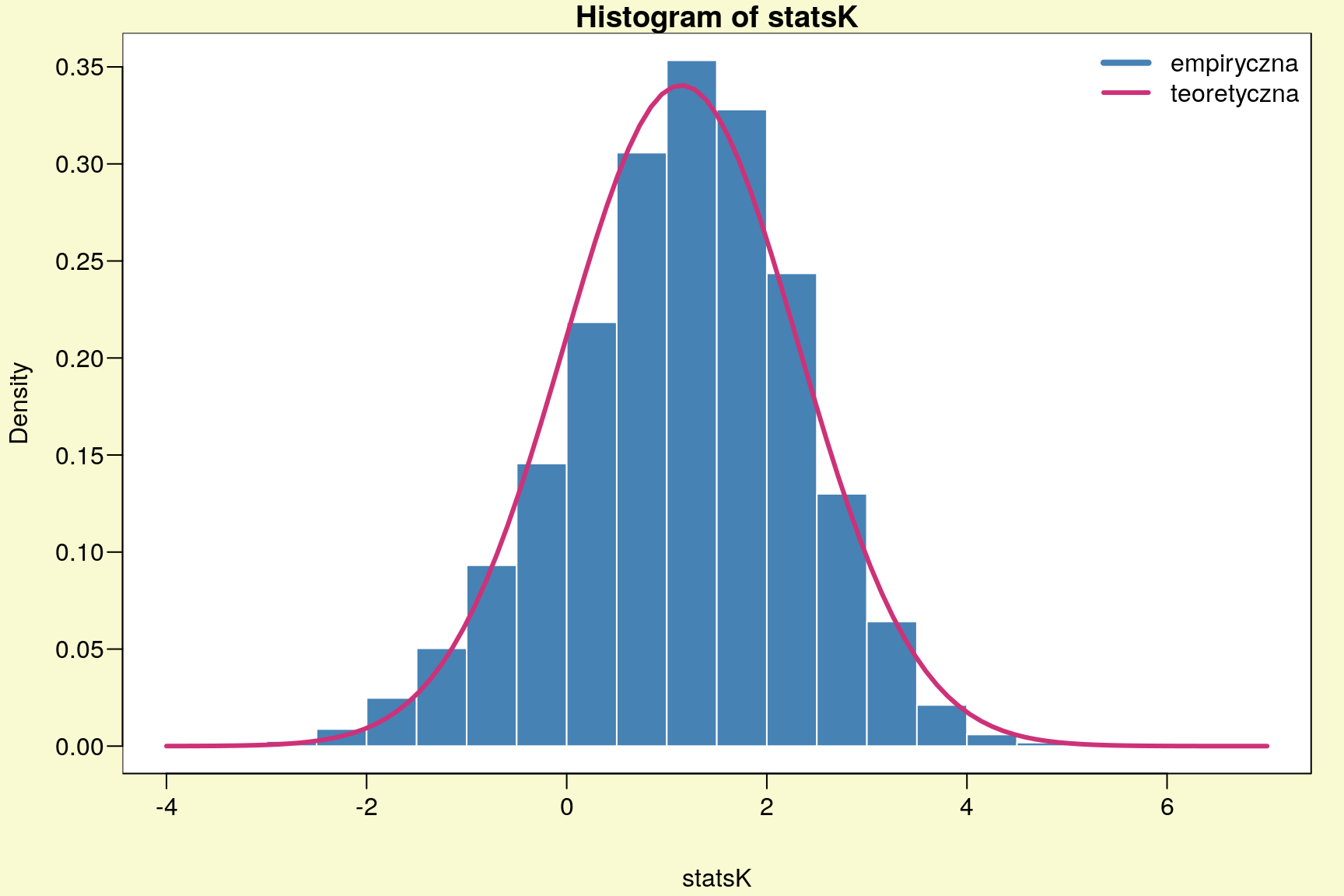
Rysunek 11.2: Rozkład statystyki z2 dla 10000 replikacji.
Na podstawie obliczonej wartości z2 dokonamy wefyfikacji następujących hipotez
statystycznych dotyczących kurtozy (wzór (11.13)):
\[
\begin{array}{ll}
H_0: & K_1 = 3\\
H_1: & K_1 \neq 3
\end{array}
\qquad\text{lub}\qquad
\begin{array}{ll}
H_0: & K_1 \geq 3\\
H_1: & K_1 < 3
\end{array}
\qquad\text{lub}\qquad
\begin{array}{ll}
H_0: & K_1 \leq 3\\
H_1: & K_1 > 3
\end{array}
\]
2*(1-pnorm(abs(z2))) # p-value dla H1: K1!=3## [1] 0.04109101pnorm(z2) # p-value dla H1: K1<3## [1] 0.97945451-pnorm(z2) # p-value dla H1: K1>3## [1] 0.02054551W przypadku weryfikacji powyższych hipotez statystycznych możemy zastosować test kurtozy Anscombe-Glynn: \[\begin{equation} a=\frac{3(n-1)}{(n+1)} \tag{11.16} \end{equation}\]
\[\begin{equation} b=\frac{24n(n-2)(n-3)}{(n+1)^2(n+3)(n+5)} \tag{11.17} \end{equation}\]
\[\begin{equation} c=\frac{6(n^2-5n+2)}{(n+7)(n+9)}\sqrt{\frac{6(n+3)(n+5)}{n(n-2)(n-3)}} \tag{11.18} \end{equation}\]
\[\begin{equation} d=6+\frac{8}{c}\left(\frac{2}{c}+\sqrt{1+\frac{4}{c}}\right) \tag{11.19} \end{equation}\]
\[\begin{equation} K_1=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^2} \tag{11.20} \end{equation}\]
\[\begin{equation} \chi=\frac{K_1-a}{\sqrt{b}} \tag{11.21} \end{equation}\]
\[\begin{equation} z=\frac{1-\frac{2}{9d}-\left(\frac{1-2/d}{1+\chi\sqrt{2/(d-4)}}\right)^{1/3}}{\sqrt{2/9d}} \tag{11.22} \end{equation}\]
moments::anscombe.test(f)##
## Anscombe-Glynn kurtosis test
##
## data: f
## kurt = 3.8046, z = 1.4585, p-value = 0.1447
## alternative hypothesis: kurtosis is not equal to 3Po wyznaczeniu wartości z1 oraz z2 możemy obliczyć statystykę testu normalności \(ep\) według wzoru:
\[\begin{equation}
ep=z_1^2+z_2^2
\tag{11.23}
\end{equation}\]
ep <- z1^2+z2^2; ep## [1] 4.282152Ponieważ statystyki z1 oraz z2 mają rozkłady zbliżone do normalnych (rys. 11.1 i rys. 11.2) to suma ich kwadratów będzie miała rozkład \(\chi^2\) z dwoma stopniami swobody.
# rozkład statystyki ep dla 10000 replikacji
statsC <- sapply(1:10000, function(i) f1(sample(ff,length(ff),TRUE))^2 +
f2(sample(ff,length(ff),TRUE))^2)par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(statsC,prob=TRUE,col='SteelBlue',border='white')
curve(dchisq(x,2),add=TRUE,lwd=3,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))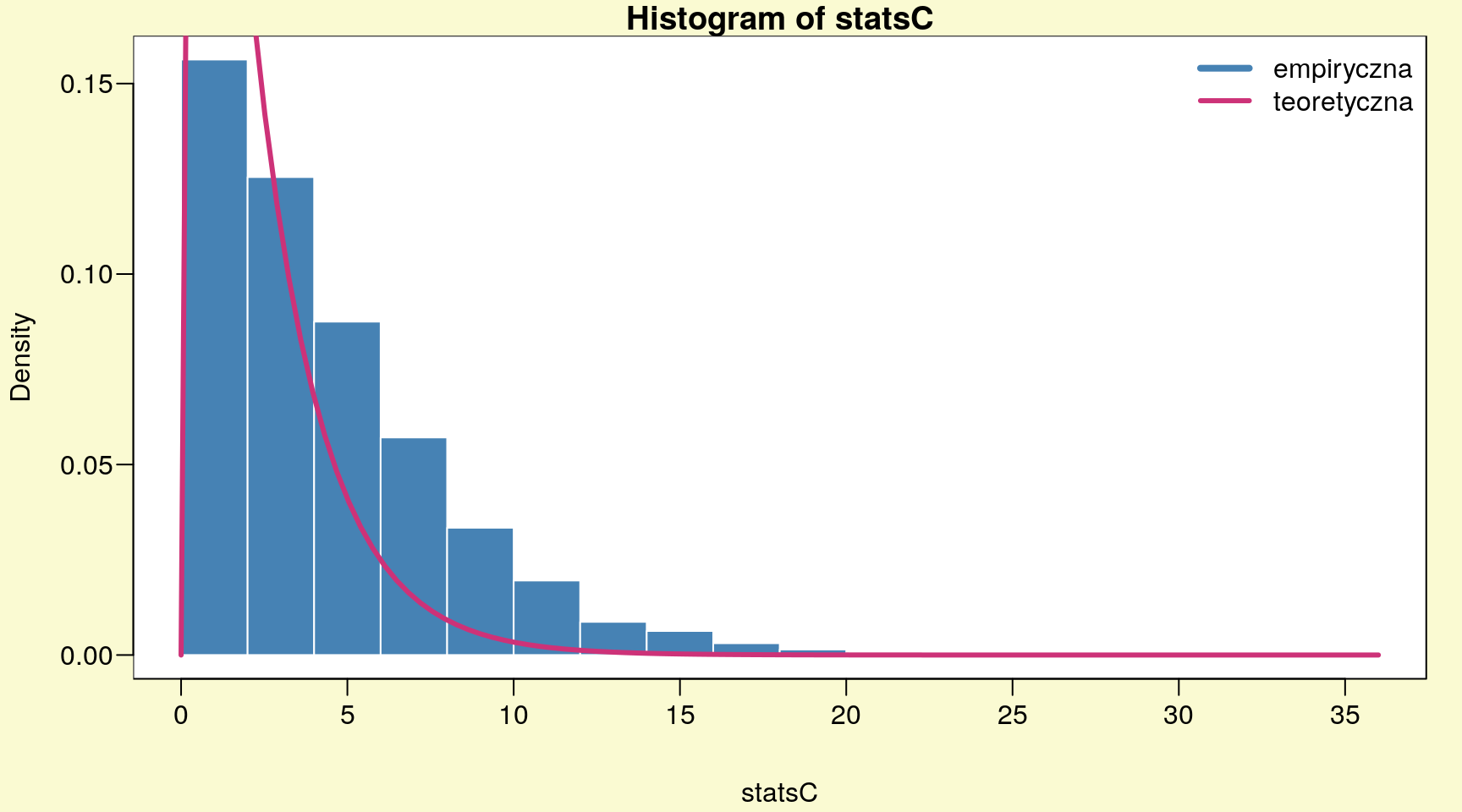
Rysunek 11.3: Rozkład statystyki ep dla 10000 replikacji.
1-pchisq(ep,2)## [1] 0.1175283Teraz zostaną przedstawione wyniki testu Doornika-Hansena z wykorzystaniem gotowej funkcji normwhn.test::normality.test1.
normwhn.test::normality.test1(as.matrix(f))## [1] "sk"
## [1] 0.1031751
## [1] "k"
## [1] 3.804592
## [1] "rtb1"
## [1] 0.1031751
## [1] "b2"
## [1] 3.804592
## [1] "z1"
## [1] 0.3315036
## [1] "z2"
## [1] 2.04261
## [1] "H0: data do not have skewness"
## [1] "pvalsk"
## [1] 0.7402641
## [1] "H0: data do not have negative skewness"
## [1] "pskneg"
## [1] 0.6298679
## [1] "H0: data do not have positive skewness"
## [1] "pskpos"
## [1] 0.3701321
## [1] "H0: data do not have kurtosis"
## [1] "pvalk"
## [1] 0.04109101
## [1] "H0: data do not have negative kurtosis"
## [1] "pkneg"
## [1] 0.9794545
## [1] "H0: data do not have positive kurtosis"
## [1] "pkpos"
## [1] 0.02054551
## [1] "H0: data are normally distributed"
## [1] "Ep"
## [,1]
## [1,] 4.282152
## [1] "dof"
## [1] 2
## [1] "sig.Ep"
## [,1]
## [1,] 0.1175283Ponieważ w teście Doornika-Hansena p-value = \(0,1175283\), należy stwierdzić, że
zmienna f (długość płatka gatunku setosa) charakteryzuje się rozkładem normalnym. Również test skośności (p-value = \(0,7402641\)) oraz kurtozy (p-value =
\(0,04109101\)) potwierdzają naszą decyzję.
shapiro.test(f)##
## Shapiro-Wilk normality test
##
## data: f
## W = 0.95498, p-value = 0.05481Także test Shapiro-Wilka wskazuje na normalność rozkładu badanej zmiennej (p-value = \(0,05481\)).
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(f,prob=TRUE,col='SteelBlue',border='white')
curve(dnorm(x,mean(f),sd(f)),add=TRUE,lwd=3,col='violetred3')
legend("topright",bg='white',bty="n",lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))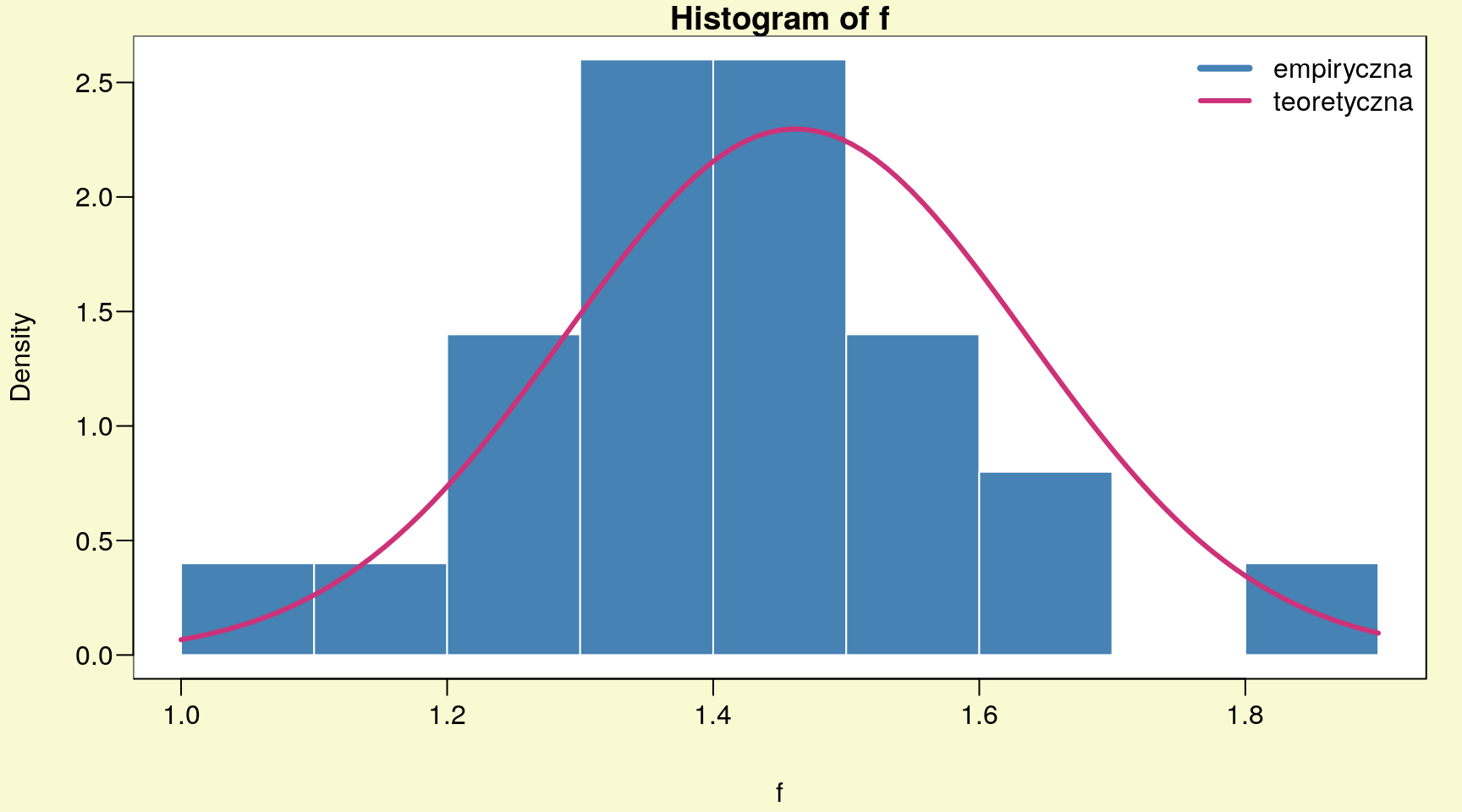
Rysunek 11.4: Histogram - długość płatka irysa, gatunek setosa.
Gdy badamy normalność za pomocą kilku testów np. Doornika-Hansena i Shapiro- Wilka zawsze warto porównać ich moc. Poniżej zostały przedstawione obliczenia dotyczące mocy obu testów.
# moc testu Doornika-Hansena:
set.seed(2305)
statP <- sapply(1:10000, function(i)
1-pchisq(f1(sample(ff,length(ff),TRUE))^2 + f2(sample(ff,length(ff),TRUE))^2,2))
mean(statP< 0.05)## [1] 0.2605# moc testu Shapiro-Wilka:
set.seed(2305)
statSW <- sapply(1:10000, function(i)
shapiro.test(sample(f,length(f),TRUE))$p.value)
mean(statSW< 0.05)## [1] 0.8758Tak więc test Shapiro-Wilka charakteryzuje się zdecydowanie większą mocą \((0,8758)\) niż test Doornika-Hansena \((0,2605)\). Czyli do oceny normalności wektora danych f należy posłużyć się testem Shapiro-Wilka.
Za pomocą funkcji normwhn.test::normality.test1 mamy możliwość także badania wielowymiarowej normalności macierzy danych. Sposób przeprowadzania obliczeń dla wielowymiarowego testu Doornika-Hansena przedstawimy na przykładzie macierzy X.
# długość i szerokość płatka - setosa:
X <- iris[1:50,3:4]
p <- length(X[1,])
n <- length(X[,1])
# wektor średnich dla kolumn macierzy X:
m <- NULL
for (i in 1:p) m[i]= mean(X[,i])W pierwszym kroku dokonamy przekształcenia macierzy X w poniższy sposób.
\[\begin{equation}
\check{X}_{p \times n}=\left[
\begin{array}{*{4}{c}}
X_{11}-\bar{X}_1 & \ldots & X_{p1}-\bar{X}_p\\
\vdots & \ddots & \vdots\\
X_{1n}-\bar{X}_1 & \ldots & X_{pn}-\bar{X}_p
\end{array}
\right]
\tag{11.24}
\end{equation}\]
M <- matrix(rep(m, n), nrow=p)
Xhat <- X-t(M)\[\begin{equation} V=\mbox{diag}\left({S_{11}}^{-1/2},\ldots,\;{S_{pp}}^{-1/2}\right) \tag{11.25} \end{equation}\]
V <- diag(1/sqrt(diag(cov(X))))\[\begin{equation} \Lambda=\mbox{diag}(\lambda_1,\ldots,\;\lambda_n) \tag{11.26} \end{equation}\]
lambda <- diag(eigen(cor(X))$values)
H <- eigen(cor(X))$vectors\[\begin{equation} R^T=H\Lambda^{-1/2}H^TV\check{X}^{T} \tag{11.27} \end{equation}\]
RT <- H %*% solve(lambda)^(1/2) %*% t(H) %*% V %*% t(Xhat)
R <- t(RT)Po otrzymaniu macierzy R możemy teraz obliczyć wartości wektorów z1 i z2 w
podobny sposób jak w przypadku testu jednowymiarowego.
# obliczenia dla z1:
f1= function(x){
DNAME <- deparse(substitute(x))
rS1 <- apply(x,2,FUN=function(x)e1071::skewness(x,type=1))
rK1 <- apply(x,2,FUN=function(x)e1071::kurtosis(x,type=1)+3)
beta <- (3*(n^2+27*n-70)*(n+1)*(n+3)) / ((n-2)*(n+5)*(n+7)*(n+9))
w2 <- -1+(2*(beta-1))^(1/2)
del <- 1/sqrt(log(sqrt(w2)))
y <- rS1*sqrt(((w2-1) / (2))*(((n+1)*(n+3))/(6*(n-2))))
z1 <- del*log(y+sqrt(y^2+1))
}
z1 <- f1(R); z1## [1] 0.3200522 3.1503286# p-value dla jednowymiarowych testów skośności - H1: S1!=0
2*(1-pnorm(abs(z1)))## [1] 0.748928767 0.001630869# obliczenia dla z2:
f2 <- function(x){
delta <- (n-3)*(n+1)*(n^2+15*n-4)
a <- ((n-2)*(n+5)*(n+7)*(n^2+27*n-70)) / (6*delta)
c <- ((n-7)*(n+5)*(n+7)*(n^2+2*n-5)) / (6*delta)
k <- ((n+5)*(n+7)*(n^3+37*n^2+11*n-313)) / (12*delta)
rS1 <- apply(x,2,FUN=function(x)e1071::skewness(x,type=1))
alpha <- a+rS1^2*c
rK1 <- apply(x,2,FUN=function(x)e1071::kurtosis(x,type=1)+3)
chi <- (rK1-1-rS1^2)*2*k
z2 <- ( (chi/(2*alpha))^(1/3)-1+(1/(9*alpha)) )*sqrt(9*alpha)
}
z2 <- f2(R); z2## [1] 2.145361 -1.685471# p-value dla jednowymiarowych testów kurtozy - H1: K1!=3
2*(1-pnorm(abs(z2)))## [1] 0.03192402 0.09189779\[\begin{equation} Ep={Z_1}^TZ_1+{Z_2}^TZ_2 \tag{11.28} \end{equation}\]
z1 <- matrix(z1,p,1)
z2 <- matrix(z2,p,1)
Ep <- t(z1) %*% z1 + t(z2) %*% z2; Ep## [,1]
## [1,] 17.47039\[\begin{equation} Ep\longrightarrow {{\chi}^{2}}_{df=2p} \tag{11.29} \end{equation}\]
1-pchisq(Ep,2*p)## [,1]
## [1,] 0.001565663Identyczne wyniki otrzymamy wykonując poniższą komendę.
normwhn.test::normality.test1(X)## [1] "sk"
## [1] 0.1031751 1.2159276
## [1] "k"
## [1] 3.804592 4.434317
## [1] "rtb1"
## [1] 0.09959901 1.14396118
## [1] "b2"
## [1] 3.872623 4.324673
## [1] "z1"
## [1] 0.3200522 3.1503286
## [1] "z2"
## [1] 2.145361 -1.685471
## [1] "H0: data do not have skewness"
## [1] "pvalsk"
## [1] 0.748928767 0.001630869
## [1] "H0: data do not have negative skewness"
## [1] "pskneg"
## [1] 0.6255356 0.9991846
## [1] "H0: data do not have positive skewness"
## [1] "pskpos"
## [1] 0.3744643837 0.0008154347
## [1] "H0: data do not have kurtosis"
## [1] "pvalk"
## [1] 0.03192402 0.09189779
## [1] "H0: data do not have negative kurtosis"
## [1] "pkneg"
## [1] 0.9840380 0.0459489
## [1] "H0: data do not have positive kurtosis"
## [1] "pkpos"
## [1] 0.01596201 0.95405110
## [1] "H0: data are normally distributed"
## [1] "Ep"
## [,1]
## [1,] 17.47039
## [1] "dof"
## [1] 4
## [1] "sig.Ep"
## [,1]
## [1,] 0.001565663Wartość p-value = \(0,001565663\) jest mniejsza od \(\alpha = 0,05\), a więc należy odrzucić
hipotezę zerową zakładającą wielowymiarowy rozkład normalny macierzy X. Warto zwrócić uwagę na wysoki wskaźnik skośności \((1,2159276)\) dla drugiej zmiennej
(szerokość płatka) co może sugerować prawostronną skośność rozkładu.
mvnormtest::mshapiro.test(t(X))##
## Shapiro-Wilk normality test
##
## data: Z
## W = 0.85492, p-value = 2.108e-05Na podstwie wielowymiarowego testu Shapiro-Wilka także należy odrzcić hipotezę
zerową zakładającą dwuwymiarowy rozkład normalny macierzy X.
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(X[,1],prob=TRUE,main="długość",border="white",col="SteelBlue")
curve(dnorm(x,mean(X[,1]),sd(X[,1])),add=TRUE,lwd=3,col="violetred3")
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
hist(X[,2],prob=TRUE,main="szerokość",border="white",col="SteelBlue")
curve(dnorm(x,mean(X[,2]),sd(X[,2])),add=TRUE,lwd=3,col="violetred3")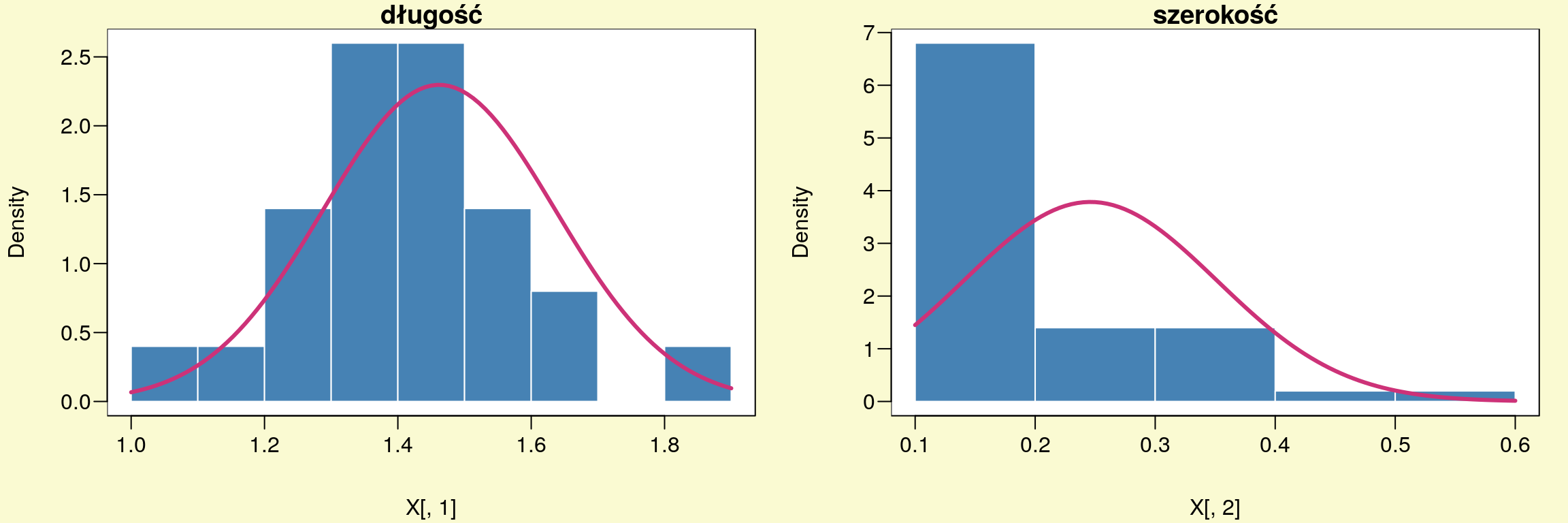
Rysunek 11.5: Długość i szerokość płatka setosa.
W celu porównania obu wielowymiaroych testów normalności obliczymy ich moc.
set.seed(2305)
statP= NULL
for (i in 1:10000) {
R1 <- matrix(c(sample(R[,1],n,TRUE),sample(R[,2],n,TRUE)),n,2)
z1 <- matrix(f1(R1))
z2 <- matrix(f2(R1))
Ep <- t(z1) %*% z1 + t(z2) %*% z2
statP[i] <- 1-pchisq(Ep, 2*p)
}
# moc wielowymiarowego testu Doornika-Hansena:
mean(statP< 0.05)## [1] 0.8919set.seed(2305)
statP= NULL
for (i in 1:10000) {
X1 <- t(matrix(c(sample(X[,1],n,TRUE),sample(X[,2],n,TRUE)),n,2))
statP[i] = mvnormtest::mshapiro.test(X1)$p.value
}
# moc wielowymiarowego testu Shapiro-Wilka:
mean(statP< 0.05)## [1] 0.8191Tym razem okazało się, że większą moc ma wielowymiarowy test Doornika-Hansena niż wielowymiarowy test Shapiro-Wilka. Różnica między mocą obu testów nie jest zbyt wysoka i wynosi \(0,0728\).
Kolejną grupa testów jaką przedstawimy to takie które badają wielowymiarową normalność w oparciu o wielowymiarowy parametr skośności lub kurtozy. Jednym z takich testów jest procedura zaproponowana przez Kanti V. Mardiego. Obliczenia dla tego testu są przedstawione poniżej. \[\begin{equation} J_n=\left[ \begin{array}{*{4}{c}} 1 \\ \vdots \\ 1 \end{array} \right] \tag{11.30} \end{equation}\]
Jn <- matrix(1, n)\[\begin{equation} I_n \tag{11.31} \end{equation}\]
In <- matrix(0, n, n)
diag(In) <- 1\[\begin{equation} D_{p \times n}=\left[ \begin{array}{*{4}{c}} d_{11} & \ldots & d_{p1}\\ \vdots & \ddots & \vdots\\ d_{1n} & \ldots & d_{pn} \end{array} \right] \tag{11.32} \end{equation}\]
Q <- In - 1/n * Jn %*% t(Jn)
X <- as.matrix(X)
D <- Q %*% X %*% solve(var(X)) %*% t(X) %*% QParametr wielowymiarowej skośności: \[\begin{equation} \hat{S}_1=\frac{1}{n^2}\sum_{p=1}^{n}\sum_{n=1}^{n}{d_{pn}}^3 \tag{11.33} \end{equation}\]
S_hat <- 1/(n^2) * sum(D^3); S_hat## [1] 1.42242Statystyka testu: \[\begin{equation} \kappa_1=\frac{n\hat{S}_1}{6} \tag{11.34} \end{equation}\]
kappa1 <- (n * S_hat)/6; kappa1## [1] 11.8535\[\begin{equation} \kappa_1\longrightarrow {{\chi}^{2}}_{df=p(p+1)(p+2)/6} \tag{11.35} \end{equation}\]
df <- p*(p+1)*(p+2)/6; df## [1] 41-pchisq(kappa1,df)## [1] 0.01847459Parametr wielowymiarowej kurtozy: \[\begin{equation} K_1=\frac{1}{n}\sum_{p=1}^{n}{d_{pp}}^2 \tag{11.36} \end{equation}\]
K_hat <- 1/n * sum(diag(D)^2); K_hat## [1] 9.305538Statystyka testu: \[\begin{equation} \kappa_2=\frac{\hat{K}_1-p(p+2)}{\sqrt{8p(p+2/n)}} \tag{11.37} \end{equation}\]
kappa2 <- (K_hat-p*(p+2)) / (8*p*(p+2)/n)^0.5; kappa2## [1] 1.153943\[\begin{equation} \kappa_2\longrightarrow N(0,1) \tag{11.38} \end{equation}\]
2*(1-pnorm(abs(kappa2)))## [1] 0.2485234Wykorzystując funkcję QuantPsyc::mult.norm mamy możliwość uzyskać jednocześnie wszystkie wartości, które zostały obliczone powyżej.
# wielowymiarowy test Mardiego w oparciu o skośność i kurtozę:
QuantPsyc::mult.norm(X)$mult.test## Beta-hat kappa p-val
## Skewness 1.422420 11.853500 0.01847459
## Kurtosis 9.305538 1.153943 0.24852335W programie R są dostępne także inne funkcje umożliwiające badanie wielowy-
miarowej normalności w oparciu o parametr skośności ICS::mvnorm.skew.test lub
kurtozy ICS::mvnorm.kur.test
# wielowymiarowy test w oparciu o skośność:
ICS::mvnorm.skew.test(X)##
## Multivariate Normality Test Based on Skewness
##
## data: X
## U = 8.2428, df = 2, p-value = 0.01622# wielowymiarowy test w oparciu o kurtozę:
ICS::mvnorm.kur.test(X, method="satterthwaite")##
## Multivariate Normality Test Based on Kurtosis
##
## data: X
## W = 3.7523, w1 = 1.5, df1 = 2.0, w2 = 2.0, df2 = 1.0, p-value =
## 0.5195Badając wielowymiarowy rozkład macierzy X w oparciu o parametr skośności należy
odrzucić hipotezę zerową (na poziomie istotności \(\alpha = 0,05\)), która zakłada rozkład
normalny. Wartości p-value są równe \(0,01847\) (test Mardiego) oraz \(0,01622\). Z kolei
na podstawie testu kurtozy p-value wynoszą: \(0,2485\) (test Mardiego) i \(0,5195\), a zatem
brak jest podstaw do odrzucenia hipotezy zerowej na poziomie istotności \(\alpha = 0,05\).
Porównanie mocy testów skośności i kurtozy:
B <- 10000
pv <- lapply(1:B, function(i) {
X1 <- matrix(c(sample(X[,1],50,TRUE),sample(X[,2],50,TRUE)),50,2);
list(QuantPsyc::mult.norm(X1)$mult.test[1,3],
ICS::mvnorm.skew.test(X1)$p.value,
QuantPsyc::mult.norm(X1)$mult.test[2,3],
ICS::mvnorm.kur.test(X1, method="satterthwaite")$p.value)
})
df <- data.frame(matrix(unlist(pv), nrow=B, byrow=T),stringsAsFactors=FALSE)
colnames(df) <- c("skewMard","skewICS","kurtMard","kurtICS")
apply(df,2,function(i) mean(i<0.05))## skewMard skewICS kurtMard kurtICS
## 0.7250 0.6932 0.2384 0.2517Na koniec przedstawimy kilka dwuwymiarowych wykresów gęstości macierzy X
za pomocą poniższych komend:
# przygotowanie zmiennych:
library(MASS)
x <- kde2d(X[,1],X[,2])$x
y <- kde2d(X[,1],X[,2])$y
z <- kde2d(X[,1],X[,2])$z
# kolory:
jet.colors= colorRampPalette(
c("blue", "cyan", "green", "yellow", "orange", "red") )
nrz <- nrow(z); ncz= ncol(z)
nbcol <- 100
color <- jet.colors(nbcol)
zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz]
facetcol <- cut(zfacet, nbcol)par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
persp(x,y,z, expand= 0.5, col= color[facetcol],xlab= "długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 210, phi= 30)
persp(x,y,z, expand= 0.5, col= color[facetcol],xlab= "długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 120, phi= 30)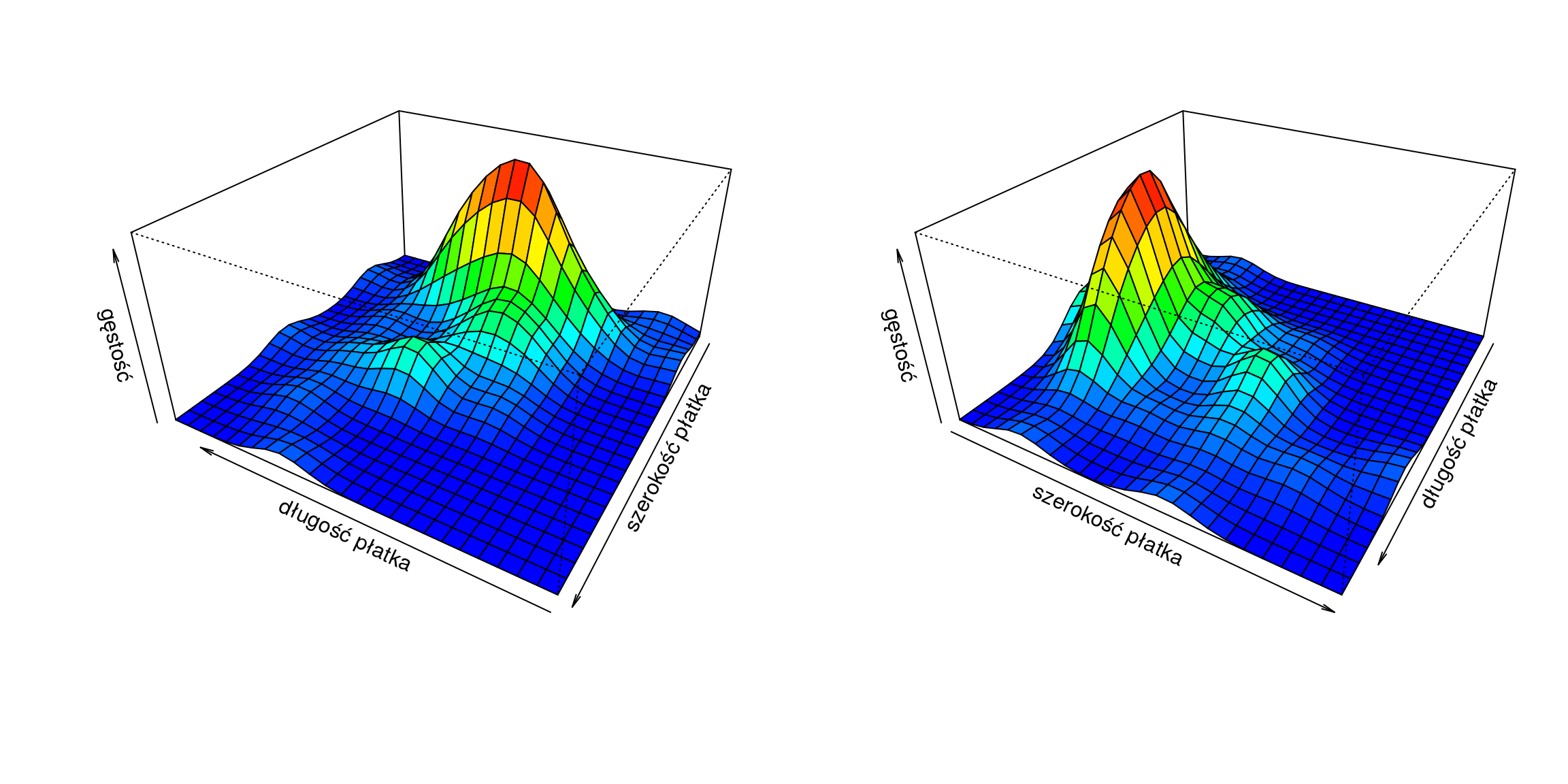
Rysunek 11.6: Gęstość empiryczna.
# tzw. mapy ciepła - gęstość empiryczna:
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
persp(x,y,z, expand = 0.5, col = color[facetcol],xlab= "długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 90, phi= 90)
persp(x,y,z, expand = 0.5, col = color[facetcol],xlab= "długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 180, phi= 90)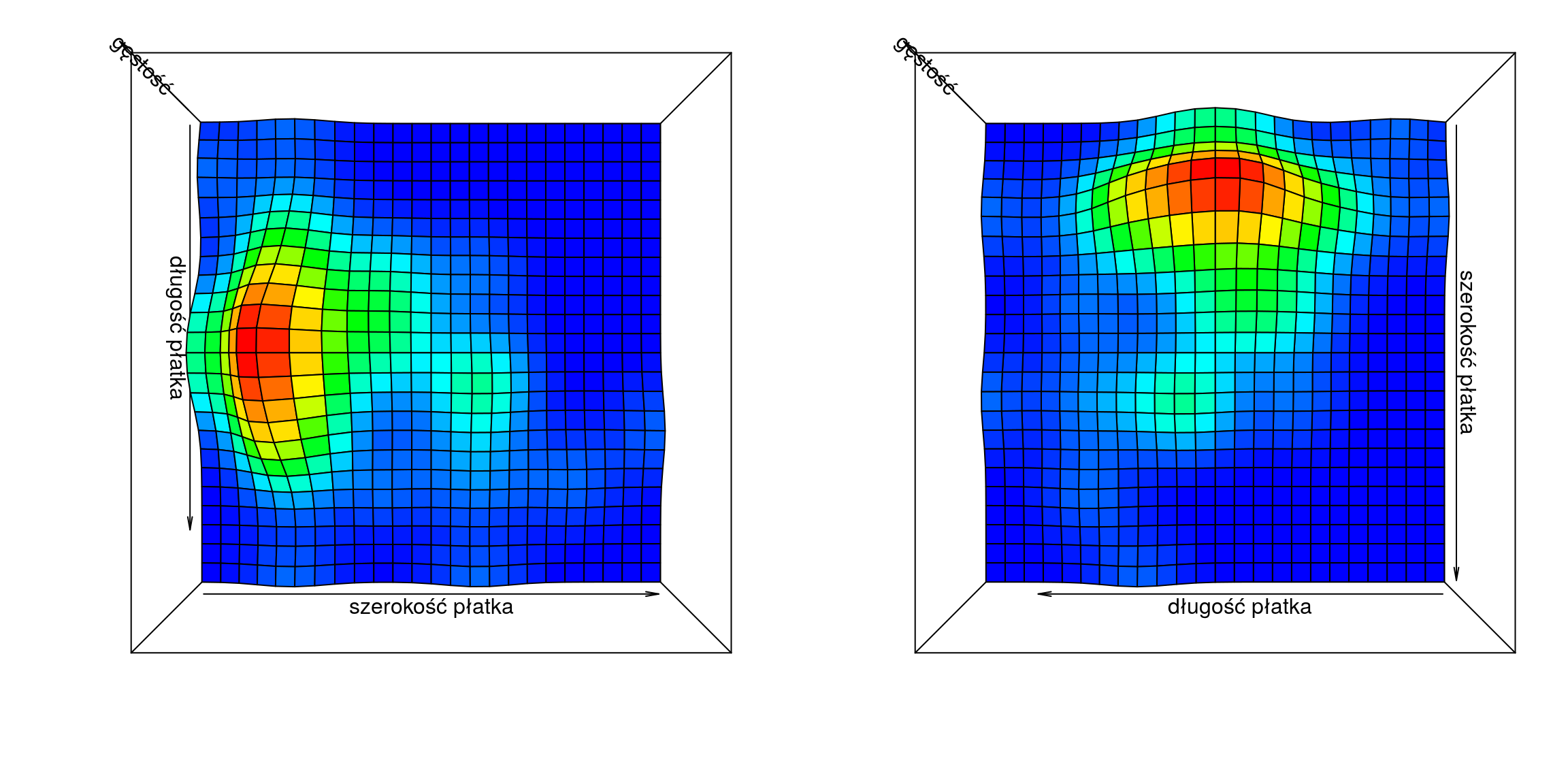
Rysunek 11.7: Gęstość empiryczna.
Możemy również przedstawić wykresy gęstości dwuwymiarowego rozkładu normalnego o określonych parametrach obliczonych na podstawie macierzy X.
mu1 <- mean(X[,1]) # średnia dla X[,1]
mu2 <- mean(X[,2]) # średnia dla X[,2]
s11 <- var(X[,1]) # wariancja dla X[,1]
s12 <- cov(X[,1],X[,2]) # kowariancja dla X[,1] i X[,2]
s22 <- var(X[,2]) # wariancja dla X[,2]
rho <- cor(X)[1,2] # korelacja między X[,1] i X[,2]
x1 <- seq(1,2,length=41) # zakres osi x
x2 <- seq(0,1,length=41) # zakres osi y
f <- function(x1,x2)
{
term1 <- 1/(2*pi*sqrt(s11*s22*(1-rho^2)))
term2 <- -1/(2*(1-rho^2))
term3 <- (x1-mu1)^2/s11
term4 <- (x2-mu2)^2/s22
term5 <- -2*rho*((x1-mu1)*(x2-mu2))/(sqrt(s11)*sqrt(s22))
term1*exp(term2*(term3+term4-term5))
}
z <- outer(x1,x2,f)
# kolory:
jet.colors= colorRampPalette(
c("blue", "cyan", "green", "yellow", "orange", "red") )
nrz <- nrow(z); ncz= ncol(z)
nbcol <- 100
color <- jet.colors(nbcol)
zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz]
facetcol <- cut(zfacet, nbcol)par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
persp(x1,x2,z, expand= 0.5, col= color[facetcol], xlab="długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 120, phi= 30)
persp(x1,x2,z, expand= 0.5, col= color[facetcol], xlab="długość płatka",
ylab= "szerokość płatka",zlab= "gęstość",theta= 90, phi= 90)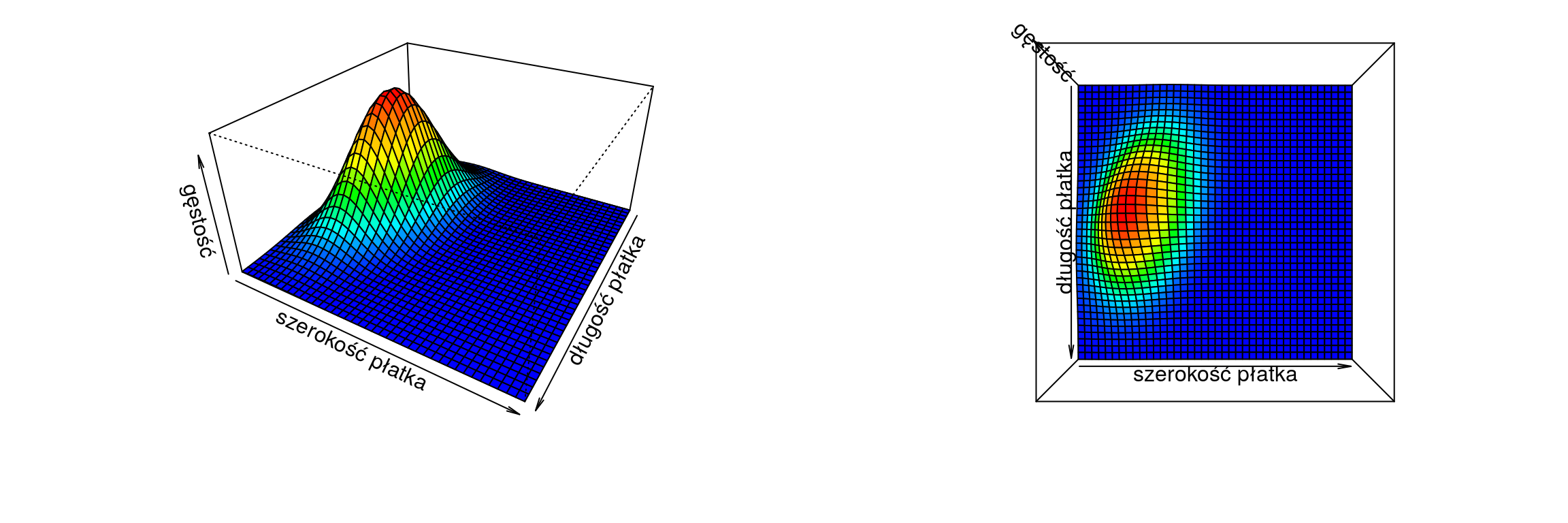
Rysunek 11.8: Gęstość teoretyczna.
W środowisku R dostępnych jest jeszcze wiele innych testów badających normalność zmiennych. Wymienimy niektóre z nich: wielowymiarowy test Doornika-
Hansena - asbio::DH.test,Energy test - energy::mvnorm.etest, Shapiro-Francia
- mvsf::mvsf. Warto także wspomnieć o gładkim teście adaptacyjnym Neymana, za
pomocą którego mamy możliwość zbadania czy wektor danych pochodzi z rozkładu
normalnego - ddst::ddst.norm.test, jednostajnego - ddst::ddst.unifrom.test,
wykładniczego - ddst::ddst.exp.test lub z rozkładu wartości ekstremalnych -
ddst::ddst.extr.test.
11.2 Testy asymptotyczne
W tym podrozdziale przedstawimy testy asymptotyczne asympTest::asymp.test,
które stanowią altenatywę dla takich testów jak: BSDA::z.test oraz var.test.
W celu przedstawienia tych testów skorzystamy ze zbioru danych, który dotyczy skuteczności leczenia niewydolności serca z rytmem zatokowym u 6800 pacjentów.
library(asympTest)
data(DIGdata)Z całego zbioru danych DIGdata wyodrębnimy dwie zmienne: DIABP - ciśnienie rozkurczliwe oraz zmienną grupującą TRTMT - leczenie (0 - placebo, 1 - lek).
t <- DIGdata[,c("DIABP","TRTMT")]
length(which(is.na(t)))## [1] 5Ponieważ nasz zbiór danych zawiera pięć obserwacji brakujących, zastąpimy je wartością mediany.
t <- e1071::impute(t,"median")
t <- as.data.frame(t)
x <- subset(t, TRTMT==0)$DIABP # podano placebo
y <- subset(t, TRTMT==1)$DIABP # podano lekJedna średnia. Weryfikacja hipotezy dotyczącej wartości średniej dla grupy pacjentów którym podano placebo: \[ \begin{array}{ll} H_0:\,\mu = 75\quad\mbox{vs.}\quad H_1:\,\mu \neq 75 \end{array} \]
asymp.test(x,par="mean",ref=75)##
## One-sample asymptotic mean test
##
## data: x
## statistic = -0.46221, p-value = 0.6439
## alternative hypothesis: true mean is not equal to 75
## 95 percent confidence interval:
## 74.54110 75.28377
## sample estimates:
## mean
## 74.91243Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że średnie ciśnienie krwi (u pacjentów którym podano placebo) wynosi 75 mmHg.
Błąd standardowy średniej:
\[\begin{equation} SE_{\bar{x}}=\sqrt{\frac{s^2}{n}} \tag{11.39} \end{equation}\] gdzie: \(s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2\) to nieobciążony estymator wariancji.
seMean(x)## [1] 0.18946Różnica dwóch średnich. Weryfikacja hipotezy o równości średnich dla dwóch grup pacjentów - pierwszej podano placebo a drugiej lek: \[ \begin{array}{ll} H_0:\,\mu_1-\mu_2 = 0\quad\mbox{vs.}\quad H_1:\,\mu_1-\mu_2 \neq 0 \end{array} \]
asymp.test(x,y,par="dMean",ref=0)##
## Two-sample asymptotic difference of means test
##
## data: x and y
## statistic = 0.069549, p-value = 0.9446
## alternative hypothesis: true difference of means is not equal to 0
## 95 percent confidence interval:
## -0.5162964 0.5542861
## sample estimates:
## difference of means
## 0.01899482Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że brak jest istotnej różnicy w średnich ciśnienia krwi dla badanych grup pacjentów.
Błąd standardowy różnicy dwóch średnich:
\[\begin{equation} SE_{\bar{x}_1-\bar{x}_2}=\sqrt{ SE^2_{\bar{x}(1)}+\rho^2\cdot SE^2_{\bar{x}(2)} } \tag{11.40} \end{equation}\] gdzie: \(SE_{\bar{x}(1)}\) i \(SE_{\bar{x}(2)}\) to błędy standardowe średnich odpowiednio dla pierwszej i drugiej grupy oraz parametr \(\rho\) to opcjonalny parametr do osłabienia/wzmocnienia udziału drugiej średniej.
seDMean(x,y)## [1] 0.2731128Iloraz dwóch średnich. Weryfikacja hipotezy o ilorazie średnich dla dwóch grup pacjentów - pierwszej podano placebo a drugiej lek: \[ \begin{array}{ll} H_0:\,\mu_1/\mu_2 = 1\quad\mbox{vs.}\quad H_1:\,\mu_1/\mu_2 \neq 1 \end{array} \]
asymp.test(x,y,par="rMean",ref=1)##
## Two-sample asymptotic ratio of means test
##
## data: x and y
## statistic = 0.06954, p-value = 0.9446
## alternative hypothesis: true ratio of means is not equal to 1
## 95 percent confidence interval:
## 0.9931053 1.0074019
## sample estimates:
## ratio of means
## 1.000254Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że brak jest istotnej różnicy w średnich ciśnienia krwi dla badanych grup pacjentów.
Błąd standardowy ilorazu dwóch średnich: \[\begin{equation} SE_{\bar{x}_1/\bar{x}_2}=\frac{1}{|\bar{x}_{(2)}|} \sqrt{ SE^2_{\bar{x}(1)}+r_0^2\cdot SE^2_{\bar{x}(2)} } \tag{11.41} \end{equation}\] gdzie: \(SE_{\bar{x}(1)}\) i \(SE_{\bar{x}(2)}\) to błędy standardowe średnich odpowiednio dla pierwszej i drugiej grupy oraz \(r0\) to iloraz dwóch średnich.
seRMean(x,y)## [1] 0.003647165Jedna wariancja. Weryfikacja hipotezy dotyczącej wartości wariancji dla grupy pacjentów którym podano placebo: \[ \begin{array}{ll} H_0:\,\sigma^2 = 120\quad\mbox{vs.}\quad H_1:\,\sigma^2 \neq 120 \end{array} \]
asymp.test(x,par="var",ref=120)##
## One-sample asymptotic variance test
##
## data: x
## statistic = 0.65419, p-value = 0.513
## alternative hypothesis: true variance is not equal to 120
## 95 percent confidence interval:
## 115.7065 128.5957
## sample estimates:
## variance
## 122.1511Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że wariancja ciśnienia krwi dla pacjentów którym podano placebo wynosi 120 mmHg.
Błąd standardowy wariancji: \[\begin{equation} SE_{s^2}=\sqrt{\frac{\sum_{i=1}^{n}\big((x_i-\bar{x})^2-s^2_*\big)^2}{n\cdot(n-1)}} \tag{11.42} \end{equation}\] gdzie: \(s^2_{*}=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\) to obciążony estymator wariancji.
seVar(x)## [1] 3.288122Różnica dwóch wariancji. Weryfikacja hipotezy o równości wariancji dla dwóch grup pacjentów - pierwszej podano placebo a drugiej lek: \[ \begin{array}{ll} H_0:\,\sigma^2_1-\sigma^2_2 = 0\quad\mbox{vs.}\quad H_1:\,\sigma^2_1-\sigma^2_2 \neq 0 \end{array} \]
asymp.test(x,y,par="dVar",ref=0)##
## Two-sample asymptotic difference of variances test
##
## data: x and y
## statistic = -1.5331, p-value = 0.1253
## alternative hypothesis: true difference of variances is not equal to 0
## 95 percent confidence interval:
## -21.183911 2.588843
## sample estimates:
## difference of variances
## -9.297534Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że brak jest istotnej różnicy w wariancjach ciśnienia krwi dla badanych grup pacjentów.
Błąd standardowy dwóch wariancji: \[\begin{equation} SE_{s_1^2-s_2^2}=\sqrt{SE_{s^2(1)}^2 +\rho^2\cdot SE_{s^2(2)}^2} \tag{11.43} \end{equation}\] gdzie: \(SE_{s^2(1)}\) i \(SE_{s^2(2)}\) to błędy standardowe wariancji odpowiednio dla pierwszej i drugiej grupy.
seDVar(x,y)## [1] 6.064589Iloraz dwóch wariancji. Weryfikacja hipotezy o równości wariancji dla dwóch grup pacjentów - pierwszej podano placebo a drugiej lek: \[ \begin{array}{ll} H_0:\,\sigma^2_1/\sigma^2_2 = 1\quad\mbox{vs.}\quad H_1:\,\sigma^2_1/\sigma^2_2 \neq 1 \end{array} \]
asymp.test(x,y,par="rVar",ref=1)##
## Two-sample asymptotic ratio of variances test
##
## data: x and y
## statistic = -1.6127, p-value = 0.1068
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.843309 1.015228
## sample estimates:
## ratio of variances
## 0.9292687Brak podstaw do odrzucenia hipotezy zerowej - możemy przyjąć, że brak jest istotnej różnicy w wariancjach ciśnienia krwi dla badanych grup pacjentów.
Błąd standardowy ilorazu wariancji: \[\begin{equation} SE_{s_1^2/s_2^2}=\frac{1}{s^{2}_{(2)}}\sqrt{ SE_{s^2(1)} +r_0^2\cdot SE_{s^2(2)}} \tag{11.44} \end{equation}\] gdzie: \(SE_{s^2(1)}\) i \(SE_{s^2(2)}\) to błędy standardowe wariancji odpowiednio dla pierwszej i drugiej grupy oraz \(s^2_{(2)}\) to nieobciążony estymator wariancji dla drugiej grupy.
seRVar(x,y)## [1] 0.0438577811.3 Testy dla proporcji
Do prezentacji testów proporcji zostaną wykorzystane dane które są dostępne na stronie internetowej GUS. Dotyczą one liczby ludności w województwie łódzkim w 2009 r. Poniżej zostały przedstawione dane dotyczące liczby osób w województwie łódzkim w 2009 r. W tym podziale została uwzględniona również struktura wiekowa.
K <- c(58548, 53251, 61402, 76522, 89106, 102074, 96932, 85084, 76663,
81355, 107911, 107430, 90269, 57402, 185898)
M <- c(61951, 56582, 64722, 80317, 92346, 106389, 100261, 87159, 75991,
84553, 99678, 92989, 72334, 41261, 95452)
w <- data.frame(K, M)
rownames(w) <- c('0-4','5-9','10-14','15-19','20-24','25-29','30-34','35-39','40-44',
'45-49','50-54','55-59','60-64','65-69','70 i więcej')par(mfcol=c(1,1),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
pyramid::pyramid(w, Llab="kobiety", Rlab="mężczyźni", Clab="wiek",
Laxis=seq(0,200000,len=5), AxisFM="d", AxisBM=".",
Lcol="orange", Rcol="red4", Csize=1, Cadj=-0.01)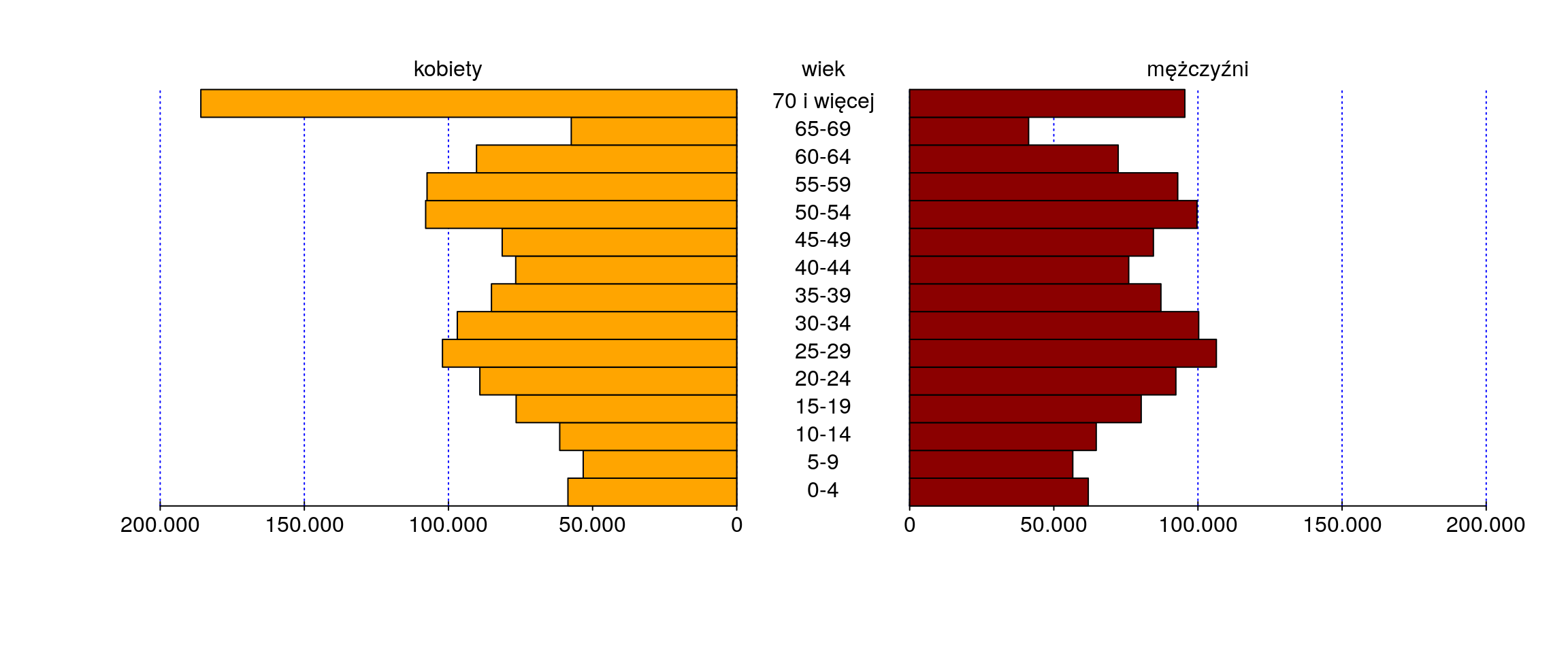
Rysunek 11.9: Liczebności w poszczególnych grupach wiekowych z podziałem na płeć.
par(mfcol=c(1,1),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
barplot(t(prop.table(as.matrix(w),1)),horiz=T,las=1,
col=c("orange","red4"))
legend('right',bg="white",fill=c('orange','red4'),c('k','m'))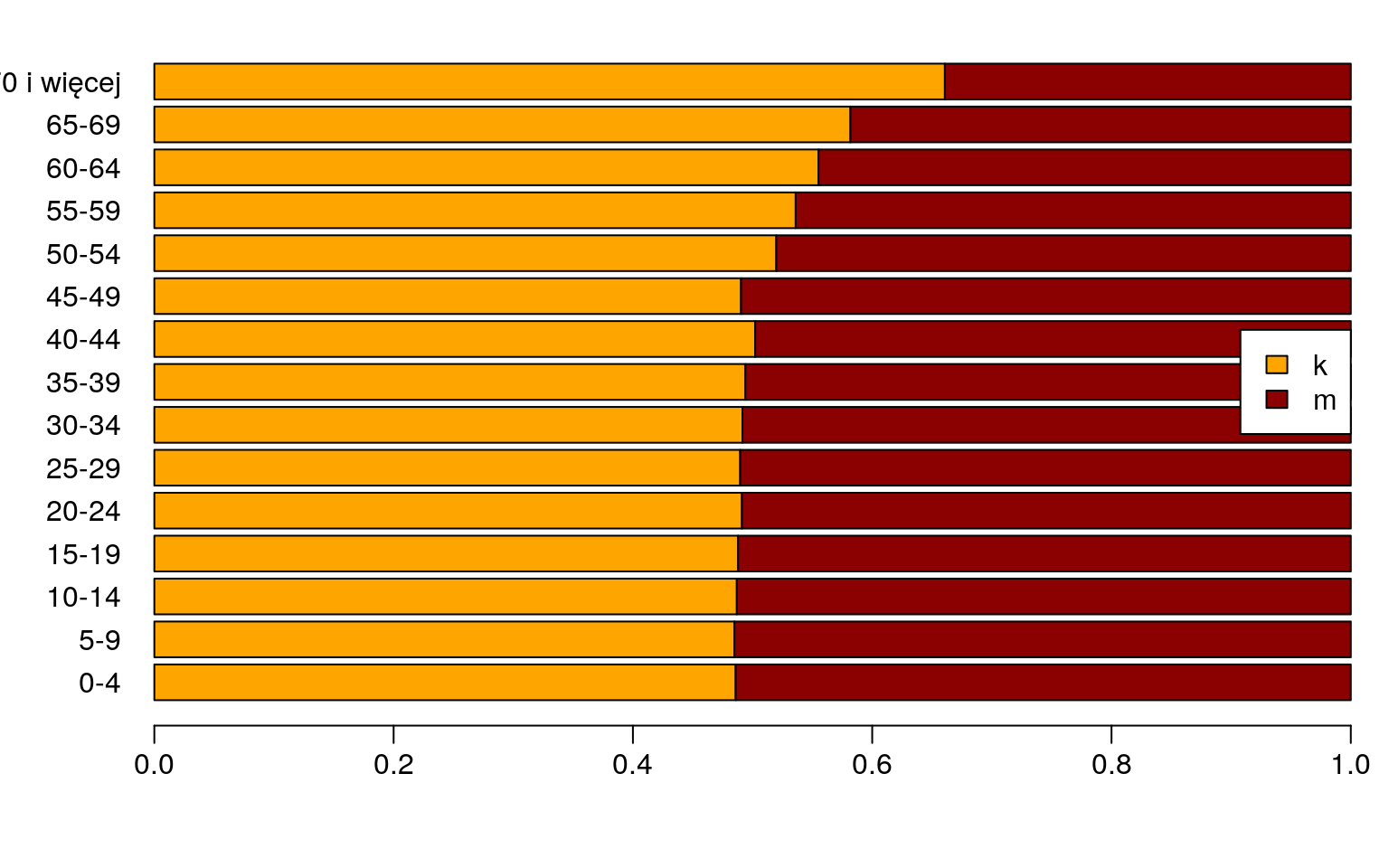
Rysunek 11.10: Prezentacja proporcji w poszczególnych grupach wiekowych.
Na podstawie danych (rys. 11.9) możemy sądzić, że odsetek kobiet i mężczyzn w grupie wiekowej 40-44 lat (rys. 11.10) może wynosić po 50%. A zatem sprawdźmy czy te proporcje są równe. Hipotezy testowe będą następującej postaci: \[H_0:\,p=0,5\quad\mbox{vs.}\quad H_1:\,p \neq 0,5\]
m <- 76663; n <- 76663+75991
binom.test(m, n, p=0.5)##
## Exact binomial test
##
## data: m and n
## number of successes = 76663, number of trials = 152650, p-value =
## 0.08591
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.4996896 0.5047125
## sample estimates:
## probability of success
## 0.5022011Na podstawie otrzymanego wyniku możemy stwierdzić, że brak jest podstaw do odrzucenia hipotezy zerowej. Tak więc na poziomie istotności \(\alpha = 0,05\) przyjmujemy, że proporcje w grupie wiekowej 40-44 lat wynoszą po \(50\%\).
P-wartość: \[\begin{equation} \sum_{}^{}{n \choose m}p^m(1-p)^{n-m} \tag{11.45} \end{equation}\]
(1-pbinom(m-1,n,.5))*2## [1] 0.08590797Przedział ufności Cloppera-Pearsona:
– z wykorzystaniem kwantyli rozkładu \(F\):
\[\begin{equation} \left(1+\frac{n-m+1}{m\,F_{\alpha/2,\;2m,\;2(n-m+1)}}\right)^{-1},\;\left(1+\frac{n-m}{(m+1)\,F_{1-\alpha/2,\;2(m+1),\;2(n-m)}}\right)^{-1} \tag{11.46} \end{equation}\]
c( 1/(1+(n-m+1)/(m*qf(0.05/2,2*m,2*(n-m+1)))),
1/(1+(n-m)/((m+1)*qf(1-0.05/2,2*(m+1),2*(n-m)))) )## [1] 0.4996896 0.5047125– z wykorzystaniem kwantyli rozkładu Beta:
\[\begin{equation} B_{[1-(1-\alpha)]/2,\;m,\;n-m+1},\quad B_{[1+(1-\alpha)]/2,m+1,\;n-m} \tag{11.47} \end{equation}\]
c( qbeta((1-(1-0.05))/2,m,n-m+1), qbeta((1+(1-0.05))/2,m+1,n-m) )## [1] 0.4996896 0.5047125Dokładny test dwumianowy warto stosować w przypadku gdy dysponujemy małymi liczebnościami. Natomiast gdy nasze liczebności są duże możemy wykorzystać inną procedurę z wykorzystaniem rozkładu normalnego lub \(\chi^2\).
Błąd standardowy proporcji: \[\begin{equation} SE_{\hat{p}}=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \tag{11.48} \end{equation}\] gdzie: \(\hat{p}\) to estymacja proporcji na podstawie próby.
Statystyka testu \(z=(\hat{p}-p_0)/SE_{\hat{p}}\) ma rozkład normalny natomiast podniesiona do kwadratu czyli \(z^2\) ma rozkład \(\chi^2\).
prop.test(m, n, correct=F)##
## 1-sample proportions test without continuity correction
##
## data: m out of n, null probability 0.5
## X-squared = 2.9582, df = 1, p-value = 0.08544
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
## 0.4996928 0.5047092
## sample estimates:
## p
## 0.5022011Przedział ufności jest obliczany według formuły Wilsona: \[\begin{equation} \frac{m+z^2}{n+z^2}-z\sqrt{p(1-p)+\frac{z^2}{4n}},\;\frac{m+z^2}{n+z^2}+z\sqrt{p(1-p)+\frac{z^2}{4n}} \tag{11.49} \end{equation}\] gdzie: \(z=z_{1-\alpha/2}\) to kwantyl z rozkładu normalnego.
Gdy pominiemy argument correct=F to otrzymamy wyniki testu z korektą ponieważ opcja correct=T jest stosowana domyślnie. Jest to korekta na ciągłość a statystyka testu ma wtedy postać: \(z=\left(|\hat{p}-p_0|-0,5\,n^{-1}\right)/SE_{\hat{p}}\).
prop.test(m, n)##
## 1-sample proportions test with continuity correction
##
## data: m out of n, null probability 0.5
## X-squared = 2.9494, df = 1, p-value = 0.08591
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
## 0.4996896 0.5047124
## sample estimates:
## p
## 0.5022011W środowisku R jest dostępnych jeszcze wiele innych przedziałow ufności dla jednej proporcji. Wymienimy niektóre z nich:
- przedział ufności Jeffreysa:
\[\begin{equation} B_{\alpha/2,\;m+1/2,\;n-m+1/2},\;B_{1-\alpha/2,\;m+1,\;n-m+1/2} \tag{11.50} \end{equation}\]
c(qbeta(0.05/2,m+1/2,n-m+0.5), qbeta(1-0.05/2,m+0.5,n-m+0.5) )## [1] 0.4996928 0.5047092- przedział ufności (asymptotyczny) Walda:
\[\begin{equation} \hat{p}-z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}},\;\hat{p}+z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \tag{11.51} \end{equation}\]
hp <- m/n
c(hp-qnorm(1-0.05/2)*sqrt(hp*(1-hp)/n),
hp+qnorm(1-0.05/2)*sqrt(hp*(1-hp)/n))## [1] 0.4996929 0.5047092- przedział ufności Agresti-Coull:
\[\begin{equation} \check{p}-z_{1-\alpha/2}\sqrt{\frac{\check{p}(1-\check{p})}{\check{n}}},\; \check{p}+z_{1-\alpha/2}\sqrt{\frac{\check{p}(1-\check{p})}{\check{n}}} \tag{11.52} \end{equation}\] gdzie: \(\check{p}=\frac{m+z_{\alpha/2}/2}{n+(z_{\alpha/2})^2}\quad\mbox{oraz}\quad \check{n}=n+z_{1-\alpha/2}\)
cp <- (m+(qnorm(1-0.05/2)^2)/2)/(n+qnorm(1-0.05/2)^2)
cn <- n+qnorm(1-0.05/2)^2
c(cp-qnorm(1-0.05/2)*sqrt((cp*(1-cp))/cn),
cp+qnorm(1-0.05/2)*sqrt((cp*(1-cp))/cn))## [1] 0.4996928 0.5047092- przedział ufności arcsine:
\[\begin{equation} \sin\left(\arcsin\sqrt{\check{p}}-\frac{z_{1-\alpha/2}}{2\sqrt{n}}\right)^2,\quad\sin\left(\arcsin\sqrt{\check{p}}+\frac{z_{1-\alpha/2}}{2\sqrt{n}}\right)^2 \tag{11.53} \end{equation}\] gdzie: \(\check{p}=\frac{m+0,375}{n+0,75}\).
cp <- (m+0.375)/(n+0.75)
c(sin(asin(sqrt(cp))+qnorm(1-0.05/2)/(2*sqrt(n)))^2,
sin(asin(sqrt(cp))-qnorm(1-0.05/2)/(2*sqrt(n)))^2)## [1] 0.5047092 0.4996928- przedział ufności logit:
\[\begin{equation} \frac{\exp\left(\lambda-z_{1-\alpha/2}\sqrt{\frac{n}{m(n-m)}}\right)}{1-\exp\left(\lambda-z_{1-\alpha/2}\sqrt{\frac{n}{m(n-m)}}\right)},\; \frac{\exp\left(\lambda-z_{1+\alpha/2}\sqrt{\frac{n}{m(n-m)}}\right)}{1-\exp\left(\lambda+z_{1-\alpha/2}\sqrt{\frac{n}{m(n-m)}}\right)} \tag{11.54} \end{equation}\] gdzie: \(\lambda=\ln\frac{m}{n-m}\).
l <- log(m/(n-m))
c(exp(l-qnorm(1-0.05/2)*sqrt(n/(m*(n-m))))/
(1+exp(l-qnorm(1-0.05/2)*sqrt(n/(m*(n-m))))),
exp(l+qnorm(1-0.05/2)*sqrt(n/(m*(n-m))))/
(1+exp(l+qnorm(1-0.05/2)*sqrt(n/(m*(n-m))))))## [1] 0.4996928 0.5047092Wszystkie omówione powyżej przedziały ufności (oraz kilka innych przedziałów)
możemy wyznaczyć dzięki funkcji MKmisc::binomCI:
# przedział ufności Wittinga:
MKmisc::binomCI(m, n, method= "witting", rand=231)##
## witting confidence interval
##
## 95 percent confidence interval:
## 2.5 % 97.5 %
## prob 0.5000651 0.5043002
##
## sample estimates:
## prob
## 0.5022011W tej części opracowania przedstawimy testy dla dwóch proporcji. Rozważane hipotezy oraz wzory dotyczące omawianego testu (bez korekty i z korektą) są przedstawione poniżej. \[H_{0}:\,p_1-p_2=0\quad\mbox{vs.}\quad H_{1}:\,p_1-p_2\neq 0\] Statystyka testu bez korekty: \[\begin{equation} z=\frac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{SE_{p(1,2)}} \tag{11.55} \end{equation}\] gdzie: \(SE_{p(1,2)}=\sqrt{\frac{m_1+m_2}{n_1+n_2}\left(1-\frac{m_1+m_2}{n_1+n_2}\right)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\).
Przedział ufności: \[\begin{equation} (\hat{p}_1-\hat{p}_2)-z_{1-\alpha/2}SE_{p(1-2)},\;(\hat{p}_1-\hat{p}_2)+z_{1-\alpha/2}SE_{p(1-2)} \tag{11.56} \end{equation}\] gdzie: \(SE_{p(1-2)}=\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\).
Do przeprowadzenia testu wykorzystamy dane dotyczące odsetka kobiet mieszkających w dwóch powiatach: piotrkowskim i mieście na prawach powiatu Piotrkowie Trybunalskim w grupie wiekowej: 70 lat i więcej.
k70 <- c(10951,5295,1970,7178,3464,3980,64883,4096,5887,5361,8865,
3856,6262,4922,3024,8276,3200,7734,3081,2676,8679,5521,2557,4180)
# liczba kobiet i mężczyzn w grupie wiekowej: 70 lat i więcej:
k70o <- c(16740,8196,3073,10922,5351,6282,94438,6296,9142,8291,13402,
6061,9697,7556,4835,12883,5050,12129,4859,4140,13147,8345,3990,6525)
# tabela:
d <- data.frame(k70,k70o)
# nazwy równań tabeli:
rownames(d) <- c('zgierski','bełchatowski','brzeziński','kutnowski',
'łaski','łęczycki','ŁÓDŹ','łódzki wsch.','łowicki','opoczyński',
'pabianicki','pajęczański','piotrkowski','PIOTRKÓW TRYB.','poddębicki',
'radomszczański','rawski','sieradzki','skierniewicki','SKIERNIEWICE',
'tomaszowski','wieluński','wieruszowski','zduńskowolski')
# wybór dwóch badanych powiatów:
d2 <- d[13:14,]; d2## k70 k70o
## piotrkowski 6262 9697
## PIOTRKÓW TRYB. 4922 7556# test dla dwóch proporcji:
prop.test(d2[,1],d2[,2],correct=F)##
## 2-sample test for equality of proportions without continuity
## correction
##
## data: d2[, 1] out of d2[, 2]
## X-squared = 0.59162, df = 1, p-value = 0.4418
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## -0.01999111 0.00871886
## sample estimates:
## prop 1 prop 2
## 0.6457667 0.6514029Statystyka testu z korektą: \[\begin{equation} z=\frac{|\hat{p}_1-\hat{p}_2|-\frac{1}{2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)-(p_1-p_2)}{SE_{p(1,2)}} \tag{11.57} \end{equation}\]
Przedział ufności: \[\begin{equation} |\hat{p}_1-\hat{p}_2|-\frac{1}{2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)z_{1-\alpha/2}SE_{p(1,2)},\;|\hat{p}_1-\hat{p}_2|+\frac{1}{2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)z_{1-\alpha/2}SE_{p(1,2)} \tag{11.58} \end{equation}\]
prop.test(d2[,1],d2[,2])##
## 2-sample test for equality of proportions with continuity
## correction
##
## data: d2[, 1] out of d2[, 2]
## X-squared = 0.56716, df = 1, p-value = 0.4514
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## -0.020108848 0.008836595
## sample estimates:
## prop 1 prop 2
## 0.6457667 0.6514029Na poziomie istotności \(\alpha = 0,05\) brak jest podstaw do odrzucenia hipotezy zerowej. Zatem należy stwierdzić, że proporcje są równe.
Za pomocą funkcji prop.test mamy także możliwość przeprowadzać
testy dla kilku proporcji. Tym razem sprawdzimy czy odsetki kobiet (w grupie wiekowej 70 lat i więcej, mieszkających w powiatach: wieluńskim, pabianickim oraz
tomaszowskim są takie same.
\[
H_{0}:\;p_1=p_2=\;\dots\,=p_k\quad\mbox{vs.}\quad H_{1}:\,\mbox{nie wszystkie proporcje są równe}
\]
Statystyka testu:
\[\begin{equation}
c=\sum_{i=1}^{k}\left(\frac{\hat{p}_i-\hat{p}}{SE_{p(i)}}\right)^2
\tag{11.59}
\end{equation}\]
gdzie: \(\hat{p}_i=\frac{m_i}{n_i},\;\hat{p}=\sqrt{\frac{\sum_{i=1}^{k}m_i}{\sum_{i=1}^{k}n_i}},\;SE_{p(i)}=\sqrt{\frac{\hat{p}(1-\hat{p})}{n_i}} \quad\mbox{dla}\quad i=1,2,\dots k\).
# wybór trzech badanych powiatów:
d3 <- d[c(11, 21, 22),]; d3## k70 k70o
## pabianicki 8865 13402
## tomaszowski 8679 13147
## wieluński 5521 8345# test dla trzech proporcji:
prop.test(d3[,1],d3[,2])##
## 3-sample test for equality of proportions without continuity
## correction
##
## data: d3[, 1] out of d3[, 2]
## X-squared = 0.068583, df = 2, p-value = 0.9663
## alternative hypothesis: two.sided
## sample estimates:
## prop 1 prop 2 prop 3
## 0.6614684 0.6601506 0.6615938Także i w tym przypadku brak jest podstaw do odrzucenia hipotezy zerowej. A zatem (na poziomie istotności \(\alpha = 0,05\)) można przyjąć, że odsetki są równe.