Rozdział 13 Modele regresji
13.1 Wprowadzenie
W tym opracowaniu zostanie przedstawionych kilka modeli regresji oraz metody za pomocą których można oszacować ich parametry. Dane jakie zostaną wykorzystane do budowy modeli regresji dotyczą przeciętnych miesięcznych wydatków i dochodów przypadających na jedną osobę w danym województwie. Informacje zostały zebrane i opublikowane przez GUS od 37302 gospodarstw domowych w 2009 roku.
wyd <- c(997.73, 1233.28, 900.35, 959.51, 826.98, 783.78, 823.56, 792.07, 937.9, 879.57,
940.2, 1013.17, 1016.33, 875.59, 977.11, 872.5) # wydatki
doch <- c(1115.1, 1438.73, 1041.73, 1114.05, 908.99, 834.59, 1018.77, 937.89, 1103.32,
1097.33, 1139.67, 1174.26, 1082.27, 1014.99, 1164.50, 1084.28) # dochody
# liczba gospodarstw domowych objętych badaniem:
gd <- c(2735,5366,3104,4381,2205,1932,1208,1258,989,3143,1627,2939,1017,1965,2039,1394)
t <- data.frame(doch,wyd)par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(doch,wyd,cex=1.2,pch=20,xlim=c(800,1550))
lines(lowess(t),lwd=2,lty=2,col="red"); grid(col="black")
legend("topleft",c("regresja lokalnie wygładzana - lowess"),lty=2,lwd=2, col="red",bg="white")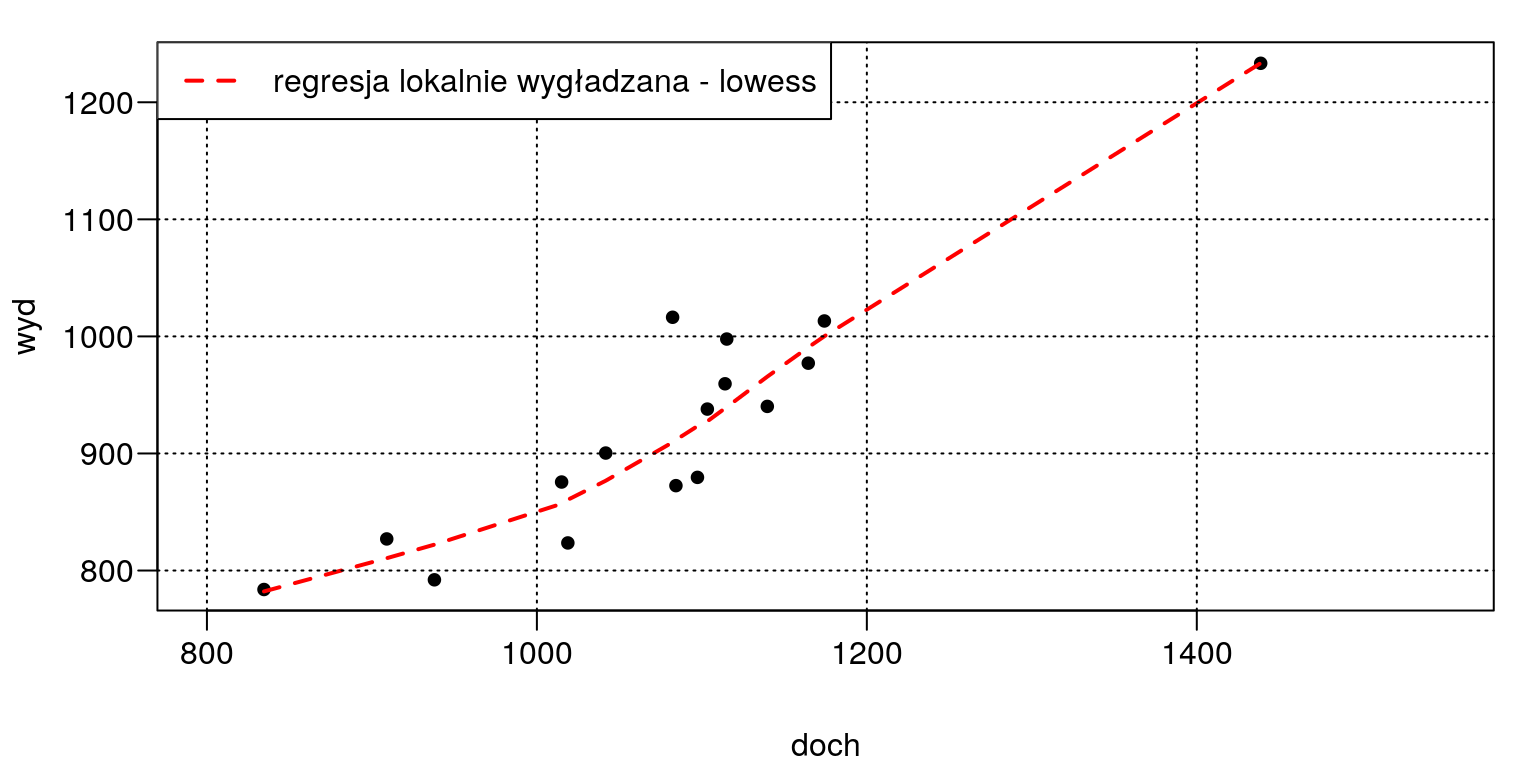
Rysunek 13.1: Wykres korelacyjny: dochód vs. wydatki.
13.2 Estymacja modelu liniowego
13.2.1 Metoda najmniejszych kwadratów
W programie R do estymacji modeli liniowych służy funkcja lm(stats). Kryterium optymalizacji dla metody najmniejszych kwadratów jest przedstawione poniżej (wzory (13.1) oraz (13.2)).
\[\begin{equation} \sum_{i=1}^{n}e_i^2 \longrightarrow\quad\mbox{min} \tag{13.1} \end{equation}\] \[\begin{equation} \sum_{i=1}^{n}(y_i-\alpha_0-\alpha_1x_{1i})^2 \longrightarrow\quad\mbox{min} \tag{13.2} \end{equation}\]
# model z wyrazem wolnym:
mnk <- lm(wyd~doch,data=t)
summary(mnk)##
## Call:
## lm(formula = wyd ~ doch, data = t)
##
## Residuals:
## Min 1Q Median 3Q Max
## -61.068 -27.713 0.374 30.364 87.274
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 96.73935 90.08070 1.074 0.301
## doch 0.76905 0.08285 9.282 2.33e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 43.1 on 14 degrees of freedom
## Multiple R-squared: 0.8602, Adjusted R-squared: 0.8502
## F-statistic: 86.15 on 1 and 14 DF, p-value: 2.332e-07Ponieważ wyraz wolny nie jest istotny statystycznie (p-value = \(0,301\)) zostanie on usunięty z modelu.
# model bez wyrazu wolnego:
mnk0 <- lm(wyd~doch+0, data=t)
summary(mnk0)##
## Call:
## lm(formula = wyd ~ doch + 0, data = t)
##
## Residuals:
## Min 1Q Median 3Q Max
## -61.267 -25.223 2.034 15.802 88.405
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## doch 0.857387 0.009962 86.07 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 43.32 on 15 degrees of freedom
## Multiple R-squared: 0.998, Adjusted R-squared: 0.9978
## F-statistic: 7407 on 1 and 15 DF, p-value: < 2.2e-16Usunięcie wyrazu wolnego spowodowało podwyższenie skorygowanego współczynnika determinacji który teraz jest równy \(0,998\). A więc model jest lepiej dopasowany. Potwierdza to także kryterium informacyjne \(AIC\) oraz \(BIC\). \[\begin{equation} AIC=n+n\ln(2\pi)+n\ln\left(\frac{RSS}{n}\right)+3k \tag{13.3} \end{equation}\]
# kryterium AIC dla modelu z wyrazem wolnym:
k <- 2; n <- length(doch)
aic <- n + n*log(2*pi) + n * log(sum(resid(mnk)^2) / n) + 3 * k
aic## [1] 169.7045# kryterium AIC dla modelu bez wyrazu wolnego:
aic0 <- n + n*log(2*pi) + n * log(sum(resid(mnk0)^2) / n) + 2 * k
aic0## [1] 168.9711# z wykorzystaniem funkcji AIC oraz parametru k:
AIC(mnk,mnk0,k=2)## df AIC
## mnk 3 169.7045
## mnk0 2 168.9711# kryterium BIC dla modelu z wyrazem wolnym:
k <- log(n)
bic <- n + n*log(2*pi) + n * log(sum(resid(mnk)^2) / n) + 3 * k
bic## [1] 172.0223# kryterium BIC dla modelu bez wyrazu wolnego:
bic0 <- n + n*log(2*pi) + n * log(sum(resid(mnk0)^2) / n) + 2 * k
bic0## [1] 170.5162AIC(mnk,mnk0,k=log(n))## df AIC
## mnk 3 172.0223
## mnk0 2 170.5162Porównamy teraz modele za pomocą funkcji anova. Badane hipotezy mają
następującą postać:
\[\begin{equation*}
\begin{array}{r@{}l}
H_0:&\;y_i=0,857387x_{1i}\\
H_1:&\;y_i=0,76905x_{1i}+96,73935
\end{array}
\end{equation*}\]
# test oparty na statystyce F:
anova(mnk0,mnk)## Analysis of Variance Table
##
## Model 1: wyd ~ doch + 0
## Model 2: wyd ~ doch
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 15 28153
## 2 14 26010 1 2142.7 1.1533 0.301# test oparty na statystyce chi-kwadrat:
anova(mnk0,mnk, test="Chisq")## Analysis of Variance Table
##
## Model 1: wyd ~ doch + 0
## Model 2: wyd ~ doch
## Res.Df RSS Df Sum of Sq Pr(>Chi)
## 1 15 28153
## 2 14 26010 1 2142.7 0.2829Takie same wyniki otrzymamy wykorzystując funkcję badającą restrykcje nałożone na parametry modelu liniowego. Czyli zweryfikujemy hipotezę zerową o nieistotności wyrazu wolnego. \[ H_0:\;\alpha_0=0\quad\mbox{vs.}\quad H_1:\;\alpha_0=0 \]
# test oparty na statystyce F:
car::linearHypothesis(mnk, c("(Intercept) = 0"))## Linear hypothesis test
##
## Hypothesis:
## (Intercept) = 0
##
## Model 1: restricted model
## Model 2: wyd ~ doch
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 15 28153
## 2 14 26010 1 2142.7 1.1533 0.301# test oparty na statystyce chi-kwadrat:
car::linearHypothesis(mnk, c("(Intercept) = 0"),test="Chisq")## Linear hypothesis test
##
## Hypothesis:
## (Intercept) = 0
##
## Model 1: restricted model
## Model 2: wyd ~ doch
##
## Res.Df RSS Df Sum of Sq Chisq Pr(>Chisq)
## 1 15 28153
## 2 14 26010 1 2142.7 1.1533 0.2829Tak więc powyższe testy potwierdziły nasz wniosek, że lepszym modelem jest regresja liniowa bez wyrazu wolnego.
plot(doch,wyd,cex=1.2,pch=20)
abline(mnk,col='red',lwd=2,lty=2); abline(mnk0,col='blue',lwd=2)
legend("topleft",c("mnk","mnk0"),col=c("red","blue"),lty=c(2,1),lwd=2)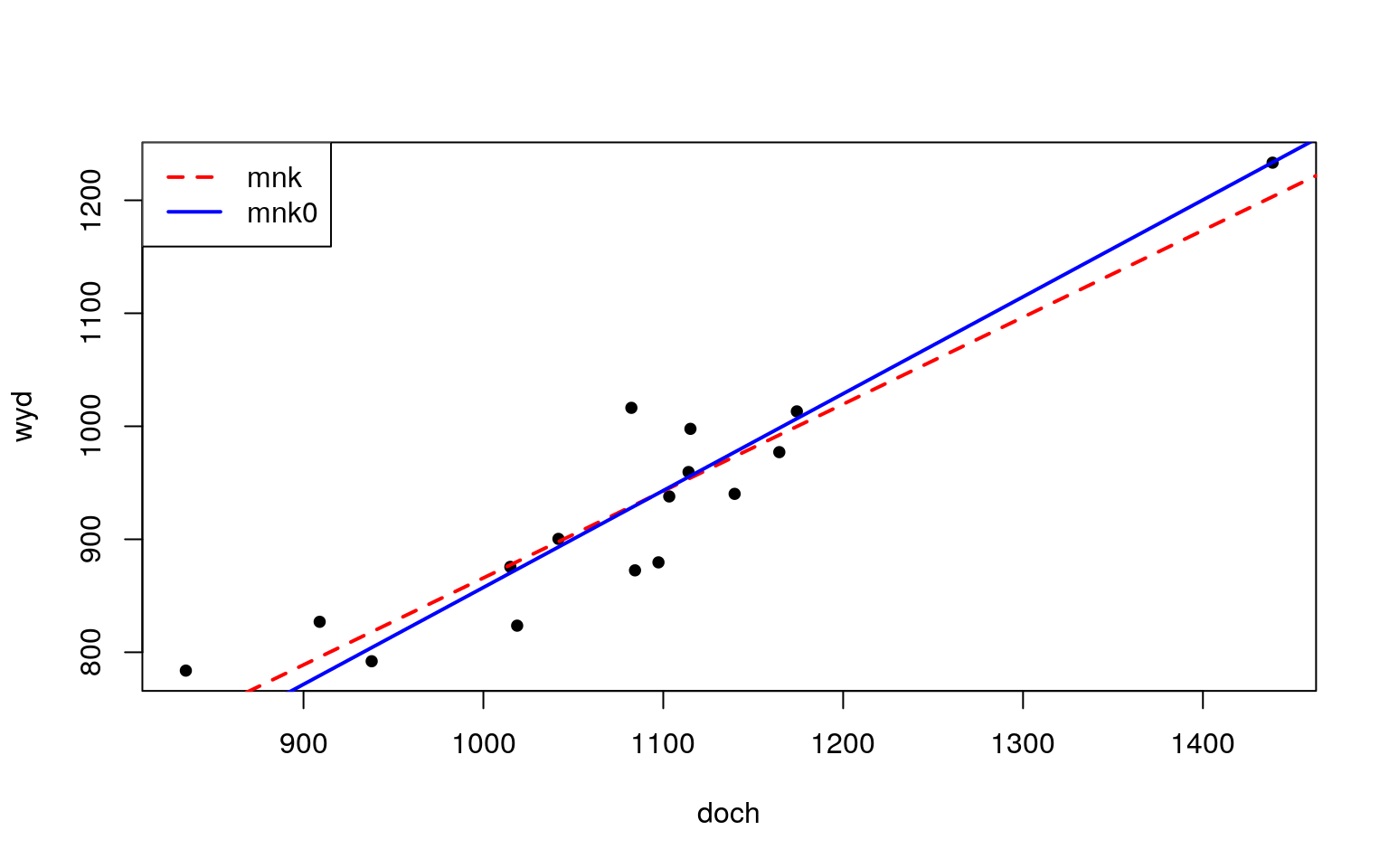
Rysunek 13.2: Regresja liniowa.
13.2.2 Poprawność specyfikacji modelu
W tym podrozdziale omówimy dwa testy badające poprawną postać analityczną modelu: test RESET oraz test Rainbow. W programie R są one dostępne w paczce lmtest. W teście RESET należy oszacować model pomocniczy o równaniu: \[\begin{equation} y_i=\alpha_1x_{1i}+\alpha_2\hat{y}_i^2+\alpha_3\hat{y}_i^3 \tag{13.4} \end{equation}\]
reset23 <- lm(wyd~doch+I(fitted(mnk0)^2)+I(fitted(mnk0)^3)+0)a następnie zweryfikować hipotezę zerową o postaci: \[\begin{equation*} H_{0}: \left[ \begin{array}{c} \alpha_{2} \\[1mm] \alpha_{3} \end{array} \right] = \left[ \begin{array}{c} 0 \\[1mm] 0 \end{array} \right] \qquad H_1: \left[ \begin{array}{c} \alpha_{2} \\[1mm] \alpha_{3} \end{array} \right] \neq \left[ \begin{array}{c} 0 \\[1mm] 0 \end{array} \right] \end{equation*}\]
Do weryfikacji powyższej hipotezy statystycznej wykorzystamy funkcję car::linearHypothesis. Umożliwia ona testowanie restrykcji nałożonych na
parametry modelu liniowego.
car::linearHypothesis(reset23,
c("I(fitted(mnk0)^2)= 0","I(fitted(mnk0)^3)= 0"), test="F")## Linear hypothesis test
##
## Hypothesis:
## I(fitted(mnk0)^2) = 0
## I(fitted(mnk0)^3) = 0
##
## Model 1: restricted model
## Model 2: wyd ~ doch + I(fitted(mnk0)^2) + I(fitted(mnk0)^3) + 0
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 15 28153
## 2 13 23446 2 4706.7 1.3049 0.3045lmtest::resettest(mnk0, power=2:3, type= "fitted")##
## RESET test
##
## data: mnk0
## RESET = 1.3049, df1 = 2, df2 = 13, p-value = 0.3045Na podstawie testu RESET stwierdzamy, że brak jest podstaw do odrzucenia hipotezy zerowej zakładającej liniowość modelu. Poniżej zostaną przedstawione także inne rodzaje tego testu. \[\begin{equation} y_i=\alpha_1x_{1i}+\alpha_2\hat{y}^2_i \tag{13.5} \end{equation}\]
lmtest::resettest(mnk0, power=2, type= "fitted")##
## RESET test
##
## data: mnk0
## RESET = 0.61343, df1 = 1, df2 = 14, p-value = 0.4465\[\begin{equation} y_i=\alpha_1x_{1i}+\alpha_2x^3_i \tag{13.5} \end{equation}\]
lmtest::resettest(mnk0, power=3, type= "fitted")##
## RESET test
##
## data: mnk0
## RESET = 0.42325, df1 = 1, df2 = 14, p-value = 0.5259Kolejnym testem który przedstawimy to test Rainbow. Służy on także do badania postaci analitycznej modelu. Poniżej zostanie zaprezentowana jego procedura obliczeniowa.
k <- 1 # liczba parametrów modelu razem z wyrazem wolnym
n <- length(doch)
doch1 <- doch[order(doch)] # sortowanie niemalejąco doch
wyd1 <- wyd[order(doch)] # sortowanie niemalejąco wyd względem dochZ tak posortowanych danych wybieramy \(50\%\) (frakcja) środkowych (centrum) obserwacji:
fraction <- 0.5 # frakcja: 50 procent obserwacji czyli 8
center <- 0.5 # centrum podziału: 50 procent
i <- 1:n # indeksy zmiennych
# początkowy indeks dla zmiennych doch1 i wyd1:
from <- ceiling(quantile(i, probs = (center - fraction/2)))
from## 25%
## 5# ostatni indeks dla zmiennych doch1 i wyd1:
to <- from + floor(fraction * n) - 1; to## 25%
## 12sy <- wyd1[from:to] # podpróba dla wyd1 o indeksach od 5 do 12
sx <- doch1[from:to] # podpróba dla doch1 o indeksach od 5 do 12
n1 <- length(sy) # liczebność podpróby
e <- resid(mnk0) # reszty dla badanego modelu mnk0
r <- resid(lm(sy~sx+0)) # reszty dla modelu z podpróby
ssr <- sum(e^2) # suma kwadratów reszt dla mnk0
ssr1 <- sum(r^2) # suma kwadratów reszt dla modelu z podpróbyStatystyka testu: \[\begin{equation} RAIN=\frac{(\sum_{i=1}^{n}e_i^2-\sum_{i=1}^{n_1}r_i^2)/(n-n_1)}{\sum_{i=1}^{n_1}r_i^2/(n_1-k)} \tag{13.6} \end{equation}\]
rain <- ((ssr - ssr1)/(n - n1))/(ssr1/(n1 - k)); rain## [1] 0.4166865df <- c((n - n1), (n1 - k))
1-pf(rain, df[1], df[2])## [1] 0.8783834lmtest::raintest(mnk0,order.by=~doch,fraction=.5,center=.5)##
## Rainbow test
##
## data: mnk0
## Rain = 0.41669, df1 = 8, df2 = 7, p-value = 0.878413.2.3 Normalność
W R jest dostępnych wiele testów badających normalność rozkładu reszt. W tym
opracowaniu zostanie przedstawiony jeden z nich. Test Andersona-Darlinga oraz
szereg innych testów normalności możemy znaleźć w bibliotece nortest. Wzór na obliczenie statystyki tego testu jest przdstawiony poniżej.
\[\begin{equation}
A=-n-\frac{1}{n}\sum_{i=1}^n(2i-1)\left(\ln(z_i)+\ln(1-z_{n+1-i})\right)
\tag{13.7}
\end{equation}\]
z <- pnorm(sort(e),mean(e),sd(e))
n <- length(e)
i <- 1:n
A <- -n-( (sum((2*i-1)*(log(z)+log(1-z[n+1-i]))))/n ); A## [1] 0.3253687Wzór poprawki na wielkość póby dla rozkładu normalnego jest podany poniżej: \[\begin{equation} A1=\left(1+\frac{0,75}{n}+\frac{2,25}{n^2}\right)A \tag{13.8} \end{equation}\]
A1 <- (1+(0.75/n)+(2.25/n^2))*A
A1## [1] 0.34348Wartości krytyczne są podawane w tablicach statystycznych np. tutaj. Można je też wyznaczyć symulacyjnie (np. \(100000\) replikacji) za pomocą funkcji PoweR::many.crit dla dowolnego poziomu istotności \(\alpha\) z uwzględnieniem liczebności próby.
set.seed(2305)
table_AD <- PoweR::many.crit(law.index= 2, stat.indices=c(2), M=10^5,
vectn=c(10,16,40,80,100),
level=c(0.05),
alter=list(stat2=3), law.pars=NULL, parstats=NULL)
table_AD## n 0.05
## [1,] 10 0.685
## [2,] 16 0.711
## [3,] 40 0.737
## [4,] 80 0.743
## [5,] 100 0.743Ponieważ wartość krytyczna (dla poziomu istotności \(\alpha = 0,05\) oraz liczebności próby \(n=16\)) wynosi \(A^* = 0,711\) i jest większa od \(A1 = 0,34348\) to należy stwierdzić, że jest brak podstaw do odrzucenia hipotezy zerowej zakładającej normalny rozkład reszt.
Dodatkowo w zależności od otrzymanej wartości \(A1\) (wzór (13.8)) należy użyć jednego z poniższych algorytmów w celu wyznaczenia wartości p-value:
- jeżeli \(A1 < 0,2\) to:
\[\begin{equation} p-value=1-\exp(-13,436+101,14\,A1-223,73\,A1^2) \tag{13.9} \end{equation}\]
- jeżeli \(0,2\leq A1<0,34\) to:
\[\begin{equation} p-value=1-\exp(-8,318+42,796\,A1-59,938\,A1^2) \tag{13.10} \end{equation}\]
- jeżeli \(0,34\leq A1 < 0,6\) to:
\[\begin{equation} p-value=\exp(0,9177-4,279\,A1-1,38\,A1^2) \tag{13.11} \end{equation}\]
- jeżeli \(A1\geq 0,6\) to:
\[\begin{equation} p-value= \exp(1,2937-5,709\,A1+0,0186\,A1^2) \tag{13.12} \end{equation}\]
W omawianym przykładzie wartość statystyki \(A1\) jest równa \(0,34348\) a zatem należy skorzystać ze wzoru (13.11).
p.value <- exp(0.9177 - 4.279 * A1 - 1.38 * A1^2 )
p.value## [1] 0.48926Teraz wykorzystamy gotową funkcje ad.ad.test:
nortest::ad.test(e)##
## Anderson-Darling normality test
##
## data: e
## A = 0.32537, p-value = 0.4893Także na podstawie adaptacyjnego testu Neymana możemy sądzić, że reszty mają
rozkład normalny. Ten test jest dostępny w paczce ddst.
set.seed(2305)
ddst::ddst.norm.test(e, compute.p=TRUE, B=1000)##
## Data Driven Smooth Test for Normality
##
## data: e, base: ddst.base.legendre, c: 100
## WT* = 0.58469, n. coord = 1, p-value = 0.441613.2.4 Heteroskedastyczność
Badanie niejednorodności wariancji w procesie resztowym zostanie zaprezentowa- ne za pomocą dwóch testów: Goldfelda-Quandta oraz Harrisona-McCabe’a. W obu przypadkach rozważane są następujące hipotezy: \[ H_0:\;\sigma^2_1=\sigma^2_2\quad\quad H_1:\;\sigma^2_1\neq \sigma^2_2 \] gdzie: \(\sigma^2_1\) i \(\sigma^2_2\) to wariancja odpowiednio w pierwszej i drugiej podpróbie. Wariancje resztowe wyznaczamy według następujących wzorów: \[\begin{equation} s_1^2=\frac{1}{(n_1-k-1)\sum_{i=1}^{n_1}e_i^2} \tag{13.13} \end{equation}\] \[\begin{equation} s_2^2=\frac{1}{(n_2-k-1)\sum_{i=1}^{n_2}e_i^2} \tag{13.14} \end{equation}\]
W pierwszej kolejności należy posortować niemalejąco zmienne względem zmiennej niezależnej doch. Należy zaznaczyć, że w przypadku zmiennych przekrojowoczasowych takie porządkowanie nie jest wymagane.
doch1 <- sort(doch) # sortowanie danych - niemalejąco
wyd1 <- wyd[order(doch)] # sortowanie danych - niemalejąco względem doch
t1 <- data.frame(wyd1,doch1)
m1 <- lm(wyd1~doch1+0,data=t1[1:8,]) # regresja dla 1 podpróby
m2 <- lm(wyd1~doch1+0,data=t1[9:16,]) # regresja dla 2 podpróby
S1 <- 1/(8-1-1)*sum(resid(m1)^2) # wariancja dla 1 podpróby
S2 <- 1/(8-1-1)*sum(resid(m2)^2) # wariancja dla 2 podpróbyStatystyka testowa w teście Goldfelda-Quandta jest następująca: \[\begin{equation} F=\frac{s_2^2}{s_1^2} \tag{13.15} \end{equation}\]
F= S2/S1; F## [1] 0.3422651lmtest::gqtest(mnk0,order.by=doch,fraction=0)##
## Goldfeld-Quandt test
##
## data: mnk0
## GQ = 0.34227, df1 = 7, df2 = 7, p-value = 0.9097
## alternative hypothesis: variance increases from segment 1 to 2Z kolei w teście Harrisona-McCabe’a statystyka będzie miała postać: \[\begin{equation} HMC=\frac{\sum_{i=1}^{s}e_i^2}{\sum_{i=1}^{n}e_i^2} \tag{13.16} \end{equation}\]
s <- 8 # liczba (odsetek) obserwacji w podpróbie
m <- lm(wyd1~doch1+0,data=t1)
rm <- resid(m)
hmc <- sum(rm[1:s]^2)/sum(rm^2)
hmc## [1] 0.7359933lmtest::hmctest(mnk0,order.by=doch,point=0.5)##
## Harrison-McCabe test
##
## data: mnk0
## HMC = 0.73599, p-value = 0.909Otrzymane wyniki na podstawie omawianych testów wskazują, że brak jest podstaw do odrzucenia \(H_0\) zakładającej homoskedastyczność reszt.
13.2.5 Obserwacje odstające
Obserwacje odstające dzielimy na: wpływowe (influential) oraz nietypowe (outliers).
Pierwsze z nich wpływają na wartości ocen parametrów modelu (czyli na kąt na-
chylenia linii regresji) a drugie na wielkości reszt (czyli na dopasowanie modelu). W
programie R dzięki funkcjom influence.measures i car::outlierTest
możemy zidentyfikować obserwacje odstające. W celu wykrycia obserwacji wpływo-
wych zostaną wykorzystane następujące wartości:
- wartości wpływu:
\[\begin{equation} h_i=\mbox{diag}\left(X(X^{T}X)^{-1}X^{T}\right) \tag{13.17} \end{equation}\] gdzie: dla \(h_i>\frac{3k}{n}\) \(i\)-tą obserwację uważa się za wpływową.
X <- as.matrix(doch)
hi <- diag((X %*% solve(t(X) %*% X) %*% t(X)))
# z wykorzystaniem gotowej funkcji:
hi <- hatvalues(mnk0) # wartości hat values- odległości Cooka:
\[\begin{equation} CD_i=\frac{e_i\, h_i}{k\,s^2(1-h_i)^2} \tag{13.18} \end{equation}\] gdzie: dla \(CD_i>F(0,05,k,n-k)\) \(i\)-tą obserwację uważa się za wpływową.
i <- 1:16 # indeksy obserwacji
k <- 1 # liczba parametrów łącznie z wyrazem wolnym
s <- summary(mnk0)$sigma # błąd standardowy reszt
s2 <- (summary(mnk0)$sigma)^2 # wariancja reszt
CDi <- (e[i]^2*hi[i])/(k*s2*(1-hi[i])^2) # odległości Cooka.
#z wykorzystaniem gotowej funkcji:
cook <- cooks.distance(mnk0) # wartości Cook’s distance- ilorazy kowariancji:
\[\begin{equation} COVRIATO_i=\left(\frac{s_{(-i)}}{s}\right)^{2k}\,\frac{1}{1-h_i} \tag{13.19} \end{equation}\] gdzie: dla \(|1-COVRATIO|>\frac{3k}{n-k}\) \(i\)-tą obserwację uważa się za wpływową.
covr <- covratio(mnk0) # wartości COVRATIO- miary \(DFFITS\):
\[\begin{equation} DFFITS_i=e_i\frac{\sqrt{h_i}}{s_{(-i)}(1-h_i)} \tag{13.20} \end{equation}\] gdzie: \(s_{(-i)}\) oznacza błąd standardowy reszt po usunięciu i-tej obserwacji ze zbioru danych:
si <- influence(mnk0)$sigmanatomiast dla \(|DFFITS_i|>3\sqrt{\frac{k}{n-k}}\) \(i\)-tą obserwację uważa się za wpływową.
dff <- dffits(mnk0) # wartości DFFITS- miary \(DFBETAS\):
\[\begin{equation} DFBETAS_i=\frac{\beta-\beta_{(-i)}}{s_{(-i)}\sqrt{(X^{T}X)^{-1}}} \tag{13.21} \end{equation}\] gdzie: \(\beta\) to oszacowany współczynnik z wykorzystaniem pełnego zbioru danych oraz \(\beta_{(-i)}\) to oszacowany współczynnik po usunięciu \(i\)-tej obserwacji ze zbioru danych:
dbetai <- influence(mnk0)$coefficientsnatomiast dla \(|DFBETAS_i|>1\) \(i\)-tą obserwację uważa się za wpływową.
dfb <- dfbetas(mnk0) # wartości DFBETASWykorzystamy teraz gotową funkcję do wyznczenia obserwacji wpływowych.
summary(influence.measures(mnk0))## Potentially influential observations of
## lm(formula = wyd ~ doch + 0, data = t) :
##
## dfb.doch dffit cov.r cook.d hat
## 2 0.00 0.00 1.20_* 0.00 0.11Zatem obserwacja dotycząca województwa mazowieckiego okazała się wpływowa na podstawie ilorazu kowariancji. Poniżej zostały przedstawione obliczenia dla wszystkich obserwacji.
influence.measures(mnk0)## Influence measures of
## lm(formula = wyd ~ doch + 0, data = t) :
##
## dfb.doch dffit cov.r cook.d hat inf
## 1 0.26381 0.26381 1.071 6.96e-02 0.0657
## 2 -0.00223 -0.00223 1.203 5.31e-06 0.1094 *
## 3 0.04075 0.04075 1.134 1.78e-03 0.0574
## 4 0.02653 0.02653 1.146 7.54e-04 0.0656
## 5 0.24256 0.24256 1.026 5.77e-02 0.0437
## 6 0.33300 0.33300 0.922 9.84e-02 0.0368
## 7 -0.28983 -0.28983 1.027 8.16e-02 0.0549
## 8 -0.06102 -0.06102 1.118 3.97e-03 0.0465
## 9 -0.04887 -0.04887 1.142 2.55e-03 0.0644
## 10 -0.39757 -0.39757 0.981 1.45e-01 0.0637
## 11 -0.23806 -0.23806 1.091 5.76e-02 0.0687
## 12 0.04143 0.04143 1.154 1.84e-03 0.0729
## 13 0.62331 0.62331 0.804 2.93e-01 0.0619
## 14 0.02947 0.02947 1.132 9.29e-04 0.0545
## 15 -0.13833 -0.13833 1.134 2.01e-02 0.0717
## 16 -0.36192 -0.36192 1.001 1.23e-01 0.0622Do identyfikacji obserwacji nietypowych możemy wykorzystać reszty standaryzowane: \[\begin{equation} e_{i(stand)}=\frac{e_i}{s\sqrt{1-h_i}} \tag{13.22} \end{equation}\] gdzie: dla \(|e_{i(stand)}|>2\) \(i\)-tą obserwację można podejrzewać o nietypowość.
es <- rstandard(mnk0) # reszty standaryzowanelub reszty studentyzowane: \[\begin{equation} e_{i(stud)}=\frac{e_{-i}}{s_{(-i)}\sqrt{1-h_i}} \tag{13.23} \end{equation}\] gdzie: dla \(|e_{i(stud)}|>2\) \(i\)-tą obserwację można podejrzewać o nietypowość.
et <- rstudent(mnk0) # reszty studentyzowaneReszty et mają rozkład t-Studenta o stopniach swobody: \(n-p-2\) (model z wyrazem
wolnym) lub \(n-p-1\) (model bez wyrazy wolnego). Zatem do identyfikacji obserwacji
odstających wykorzystamy p-value tego rozkładu weryfikując następukące hipotezy
statystyczne:
\[
H_{0}:\,i\mbox{-ta obserwacja jest typowa}\quad H_{1}:\,i\mbox{-ta obserwacja jest nietypowa}
\]
Dla obserwacji o największej wartości bezwzględnej et statystyka testu będzie miała postać:
\[\begin{equation}
\mbox{max}|e_{i(stud)}|
\tag{13.24}
\end{equation}\]
# p-value z rozkładu t-Studenta:
p.value <- 2*(1-pt( max(abs(et)) ,16-1-1))
p.value## [1] 0.02937727# poprawka Bonferonniego:
Bp.value= 16*p.value
Bp.value## [1] 0.4700364# wykorzystanie funkcji outlierTest:
car::outlierTest(mnk0)## No Studentized residuals with Bonferonni p < 0.05
## Largest |rstudent|:
## rstudent unadjusted p-value Bonferonni p
## 13 2.425829 0.029377 0.47004Ponieważ p-value = \(0,47004\) to na poziomie istotności \(\alpha = 0,05\) brak jest podstaw do odrzucenia \(H_0\) . Gdy dodamy odpowiednie argumenty do funkcji car::outlierTest, to otrzymamy uporządkowane malejąco wartości \(|e_{i(stud)}|\) oraz p-value.
car::outlierTest(mnk0,order=T,cutoff=Inf,n.max=Inf)## Warning in if (order) order(bp) else 1:n: warunek posiada długość > 1 i
## tylko pierwszy element będzie użyty## rstudent unadjusted p-value Bonferonni p
## 13 2.425829301 0.029377 0.47004
## 6 1.702938479 0.110670 NA
## 10 -1.524648740 0.149610 NA
## 16 -1.405761385 0.181600 NA
## 7 -1.202794661 0.249000 NA
## 5 1.134839609 0.275500 NA
## 1 0.994454997 0.336880 NA
## 11 -0.876672700 0.395460 NA
## 15 -0.497741566 0.626390 NA
## 8 -0.276280971 0.786370 NA
## 9 -0.186335919 0.854850 NA
## 3 0.165166434 0.871170 NA
## 12 0.147748037 0.884650 NA
## 14 0.122770528 0.904030 NA
## 4 0.100105764 0.921680 NA
## 2 -0.006351306 0.995020 NAW dignostyce modelu ekonometrycznego bardzo pomocnym narzędziem są również wykresy, które można wygenerować za pomocą komendy:
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
par(mfrow=c(2,2))
plot(mnk0)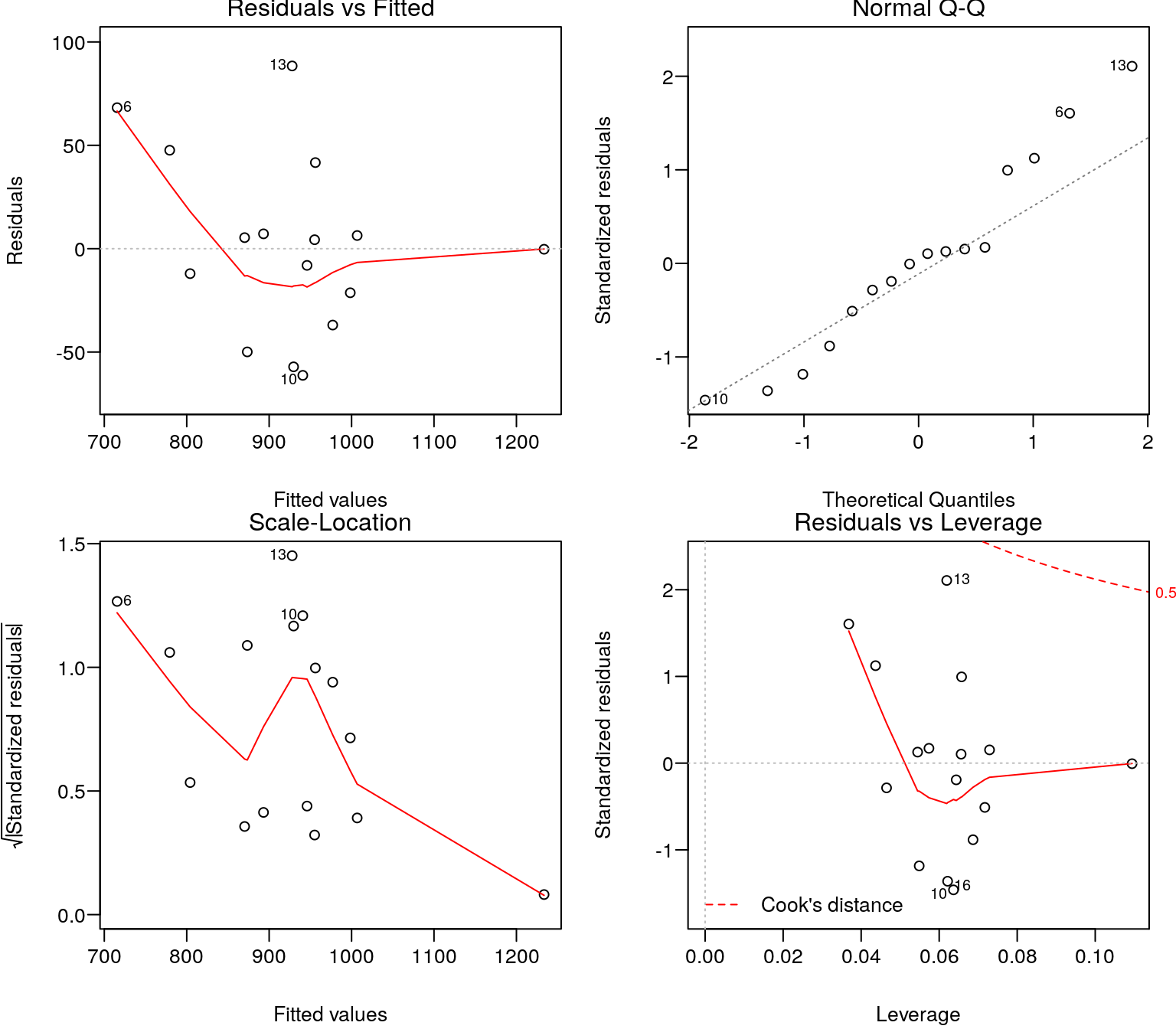
Rysunek 13.3: Diagnostyka modelu.
13.2.6 Metoda najmniejszych wartości bezwzględnych
Jeśli w zbiorze danych występują obserwacje odstające to należy je wyeliminować lub zastosować regresję kwantylową. Dla parametru \(\tau = 0,5\) (mediana) otrzymujemy estymator metody najmniejszego odchylenia bezwzględnego, którego kryterium optymalizacji jest przedstawione poniżej (wzory 13.26a oraz 13.26b).# model z wyrazem wolnym:
q <- quantreg::rq(wyd~doch,tau=0.5)
summary(q, se='nid')##
## Call: quantreg::rq(formula = wyd ~ doch, tau = 0.5)
##
## tau: [1] 0.5
##
## Coefficients:
## Value Std. Error t value Pr(>|t|)
## (Intercept) 18.81043 138.88795 0.13544 0.89420
## doch 0.84413 0.12837 6.57568 0.00001# model bez wyrazu wolnego:
q0 <- quantreg::rq(wyd~doch+0,tau=0.5)
summary(q0,se='nid')##
## Call: quantreg::rq(formula = wyd ~ doch + 0, tau = 0.5)
##
## tau: [1] 0.5
##
## Coefficients:
## Value Std. Error t value Pr(>|t|)
## doch 0.85720 0.01716 49.95465 0.00000par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(doch,wyd,cex=1.2,pch=20)
abline(q,col='red',lwd=2,lty=2); abline(q0,col='blue',lwd=2)
legend("topleft",c("q","q0"),col=c("red","blue"),lty=c(2,1),lwd=2)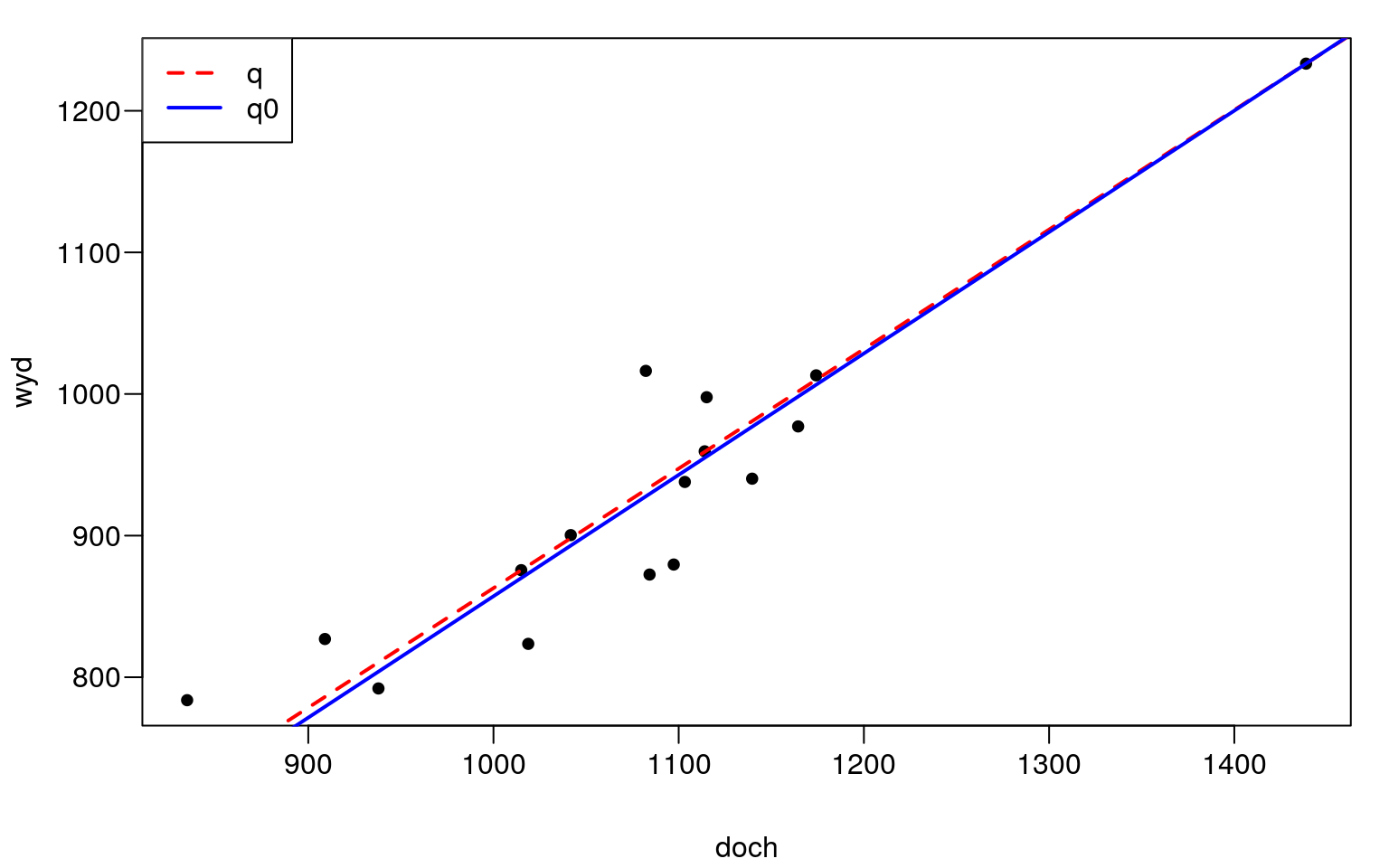
Rysunek 13.4: Regresja kwantylowa.
13.3 Estymacja modelu nieliniowego
13.3.1 Model kwadratowy
Pierwszą funkcją nieliniową jaką spróbujemy dopasować do naszych danych będzie model kwadratowy: \[\begin{equation} y=\alpha_0+\alpha_1x^2 \tag{13.25} \end{equation}\] Estymację parametrów funkcji o wzorze (13.25) dokonamy za pomocą poniższej komendy:
k <- lm(wyd~I(doch^2),data=t)
summary(k)##
## Call:
## lm(formula = wyd ~ I(doch^2), data = t)
##
## Residuals:
## Min 1Q Median 3Q Max
## -54.857 -27.803 1.452 19.653 93.152
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.218e+02 4.206e+01 12.404 6.11e-09 ***
## I(doch^2) 3.427e-04 3.453e-05 9.924 1.03e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 40.67 on 14 degrees of freedom
## Multiple R-squared: 0.8755, Adjusted R-squared: 0.8667
## F-statistic: 98.49 on 1 and 14 DF, p-value: 1.026e-07par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(t,cex=1.2,pch=20)
curve(coef(k)[1]+coef(k)[2]*x^2,add=TRUE,col="red",lwd=2)
abline(mnk0,col="orange",lty=1,lwd=2)
legend("topleft",c("k","mnk0"),col=c("red","orange"),lty=1,lwd=2)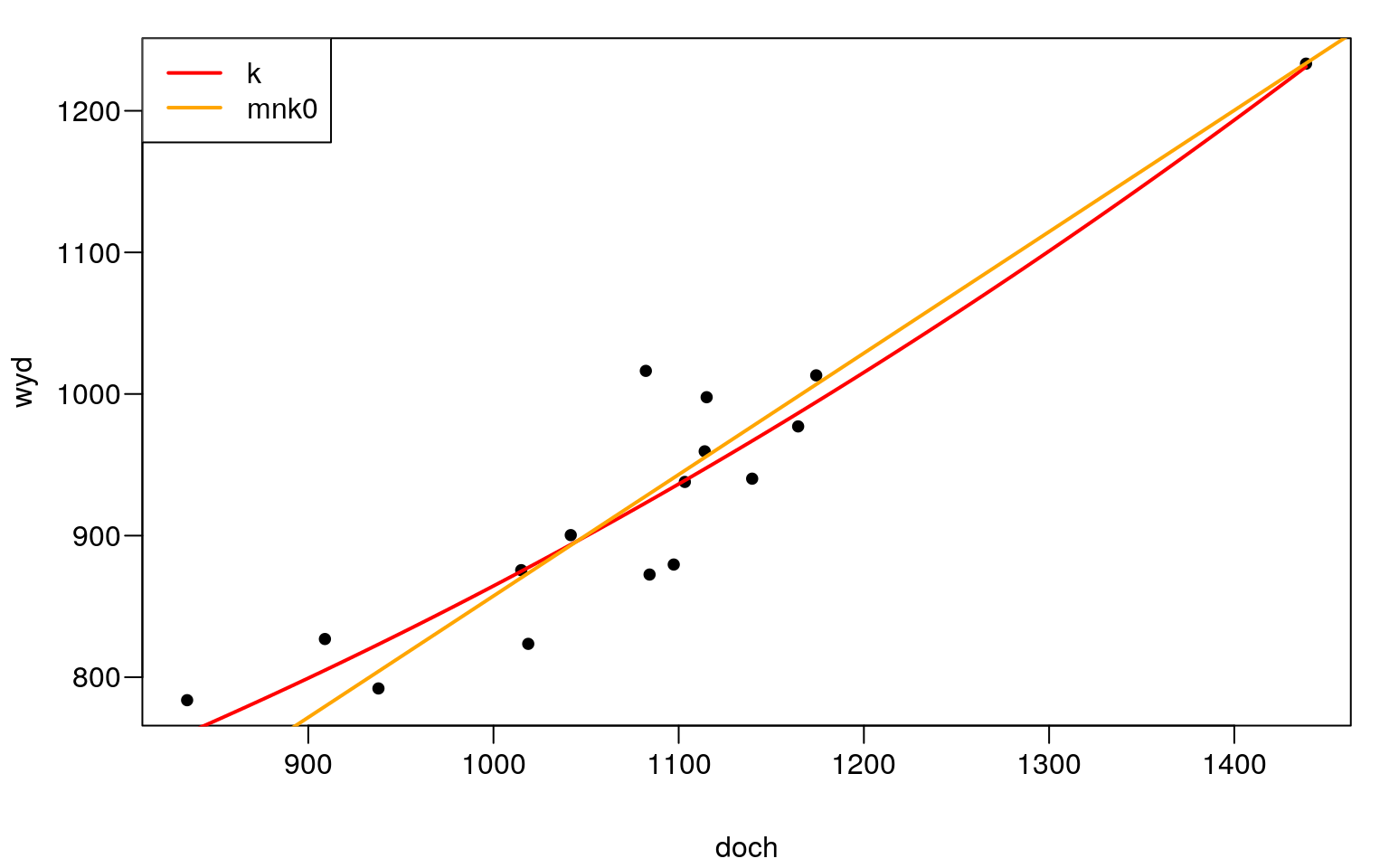
Rysunek 13.5: Regresja liniowa i kwadratowa.
AIC(mnk0,k)## df AIC
## mnk0 2 168.9711
## k 3 167.8451sapply(c(900,1000,1100,1200), function(x) 0.000685408*x)## [1] 0.6168672 0.6854080 0.7539488 0.8224896Otrzymane wartości można zinterpretować w następujący sposób. Wydatki w przeliczeniu na jedną osobę rosły średnio o 0, \(62\)zł na jedną złotówkę przyrostu dochodów, przy poziomie dochodów równych 900zł. Natomiast prz poziomie dochodów równych \(1200\)zł wydatki rosły średnio o \(0,82\)zł na złotówkę przyrostu dochodów.
13.3.2 Model wykładniczy
Analityczna postać funkcji wykładniczej jest podana poniżej: \[\begin{equation} y=\alpha_0\alpha_1x^x \tag{13.26} \end{equation}\] gdzie: \(\alpha_0>0\) oraz \(\alpha_1>0\) i \(\alpha_1\neq 1\)
Aby oszacować parametry modelu nieliniowego z wykorzystaniem funkcji nls
(nieliniowa metoda najmniejszych kwadratów) należy znaleźć parametry startowe.
Można je wyznaczyć sprowadzając funkcję nieliniową do postaci liniowej.
\[\begin{equation}
\ln y = \beta_0 \beta_1 x
\tag{13.27}
\end{equation}\]
mw <- lm(log(wyd)~doch)
summary(mw)##
## Call:
## lm(formula = log(wyd) ~ doch)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.063814 -0.029988 0.003799 0.022039 0.096239
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.971e+00 9.313e-02 64.115 < 2e-16 ***
## doch 7.916e-04 8.566e-05 9.241 2.46e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.04456 on 14 degrees of freedom
## Multiple R-squared: 0.8591, Adjusted R-squared: 0.8491
## F-statistic: 85.39 on 1 and 14 DF, p-value: 2.462e-07W kolejnym kroku obliczymy parametry funkcji wykładniczej według wzorów: \(\alpha_0=\exp(\beta_0)\) oraz \(\alpha_1=\exp(\beta_1)\).
b0 <- exp(coef(mw)[1])
b0## (Intercept)
## 391.9122b1 <- exp(coef(mw)[2])
b1## doch
## 1.000792Otrzymane wartości można wykorzystać jako parametry startowe w nieliniowej metodzie najmniejszych kwadratów.
w <- nls(wyd~a0*a1^doch,start=list(a0=b0,a1=b1),data=t)
summary(w)##
## Formula: wyd ~ a0 * a1^doch
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## a0 3.873e+02 3.346e+01 11.58 1.48e-08 ***
## a1 1.001e+00 7.733e-05 12942.47 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 40.84 on 14 degrees of freedom
##
## Number of iterations to convergence: 2
## Achieved convergence tolerance: 1.024e-06AIC(k,w)## df AIC
## k 3 167.8451
## w 3 167.9795(coef(w)[2]-1)*100## a1
## 0.08034964Interpretacja otrzymanych parametrów jest następująca. Jeżeli dochód wzrośnie o \(1\)zł to wydatki również wzrosną o \(0,08\%\).
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(t,cex=1.2,pch=20)
curve(coef(k)[1]+coef(k)[2]*x^2,add=TRUE,col="red",lwd=2)
curve(coef(w)[1]*coef(w)[2]^x,add=TRUE,col="orange",lty=2,lwd=2)
legend("topleft",c("k","w"),col=c("red","orange"),lty=c(1,2),lwd=2)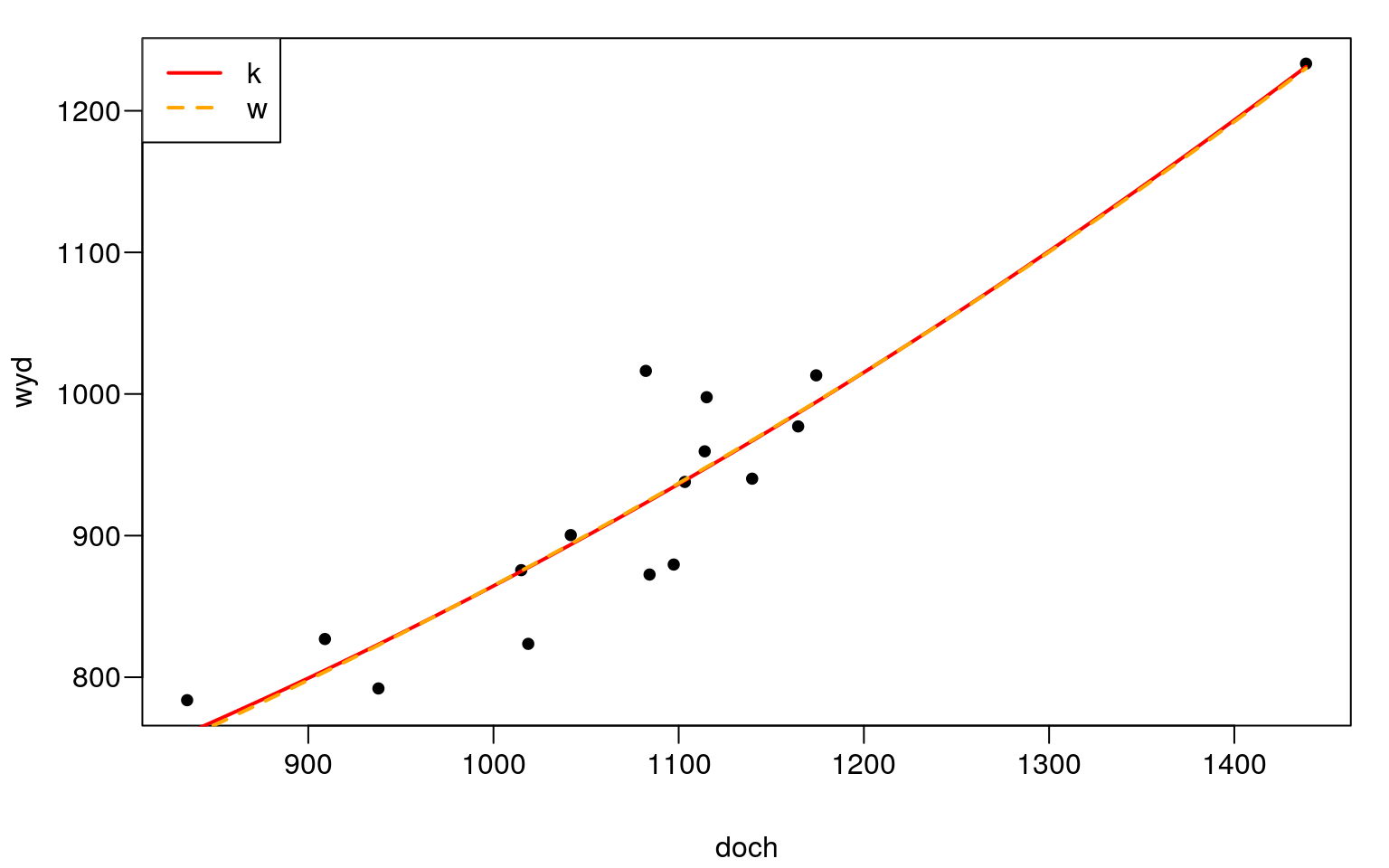
Rysunek 13.6: Regresja kwadratowa i wykładnicza.
13.3.3 Model hiperboliczny
Kolejną funkcją jaką będziemy badać to model hiperboliczny o postaci: \[\begin{equation} y=\frac{\alpha_0x^2}{x+\alpha_1} \tag{13.28} \end{equation}\] Parametry startowe wyznaczymy za pomocą następującego wzoru: \[\begin{equation} \frac{1}{y}=\beta_1\frac{1}{x}+\beta_2\frac{1}{x^2} \tag{13.29} \end{equation}\] gdzie: \(\alpha_0=\frac{1}{\beta_1}\) oraz \(\alpha_1=\frac{\beta_2}{\beta_1}\).
mh <- lm(I(1/wyd)~I(1/doch)+I(1/doch^2)+0)
summary(mh)##
## Call:
## lm(formula = I(1/wyd) ~ I(1/doch) + I(1/doch^2) + 0)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.731e-05 -3.285e-05 -1.201e-06 3.315e-05 7.973e-05
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## I(1/doch) 1.4011 0.1151 12.172 7.79e-09 ***
## I(1/doch^2) -249.8795 118.3491 -2.111 0.0532 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.116e-05 on 14 degrees of freedom
## Multiple R-squared: 0.9981, Adjusted R-squared: 0.9978
## F-statistic: 3682 on 2 and 14 DF, p-value: < 2.2e-16b1 <- 1/coef(mh)[1]
b1## I(1/doch)
## 0.713737b2 <- coef(mh)[2]/coef(mh)[1]
b2## I(1/doch^2)
## -178.3482h <- nls(wyd~(a0*doch^2)/(doch+a1),start=list(a0=b1,a1=b2))
summary(h)##
## Formula: wyd ~ (a0 * doch^2)/(doch + a1)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## a0 0.77328 0.06732 11.487 1.63e-08 ***
## a1 -107.24575 84.78736 -1.265 0.227
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 43 on 14 degrees of freedom
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 4.685e-06Ponieważ parametr \(\alpha_1\) jest nieistotny statystycznie, a więc gdy go pominiemy to funkcja hiperboliczna sprowadzi się do modelu liniowego: \[ y=\frac{\alpha_0x^2}{x+\alpha_1}=\frac{\alpha_0x^2}{x+0}=\frac{\alpha_0x^2}{x}=\frac{\alpha_0x}{1}=\alpha_0x \]