Rozdział 12 Przykład analizy liczby przestępstw w Polsce w 2009 r.
12.1 Wprowadzenie
Do analizy liczby przestępstw w Polsce wykorzystamy dane które są dostępne w bazie danych GUS. Tabela przedstawia liczbę przestępstw stwierdzonych w zakończonych postępowaniach przygotowawczych w 2009 roku.
krym <- c(77967, 36815, 49457, 31104, 22182, 62488, 103680, 18582, 23852, 16086,
53998, 117557, 18725, 25482, 66610, 39012)
gosp <- c(11169, 10337, 5870, 4854, 5506, 11824, 14045, 2648, 4551, 2561,
26185, 19481, 9108, 4943, 12425, 5758)
zyc_zdr <- c(2705, 1396, 1957, 1604, 1073, 2496, 3496, 923, 1326, 1015, 2437,
5050, 879, 1506, 2410, 1435)
wol <- c(4498, 1883, 2765, 1849, 1628, 4009, 4225, 1421, 1597, 921, 3511,
6670, 921, 1498, 3818, 2160)
rodz_opie <- c(3430, 1669, 3191, 3086, 1109, 2751, 5041, 1210, 1486, 923,
1723, 6853, 1267, 1805, 3123, 1099)
mien <- c(60385, 33400, 34622, 22119, 16262, 47333, 81870, 13896, 17535, 11940,
46273, 93888, 16267, 19794, 45119, 30558)
drog <- c(15936, 8931, 12362, 10011, 7403, 10330, 21876, 5578, 7961, 5696,
8341, 14934, 6180, 6575, 15134, 10900)
woj <- c("dolnośląskie", "kuj_pom", "łódzkie", "lubelskie", "lubuskie", "małopolskie",
"mazowieckie", "opolskie", "podkarpackie", "podlaskie", "pomorskie", "śląskie",
"świętokrzyskie", "war_mazur", "wielkopolskie", "zach_pomorskie")
G <-data.frame(krym,gosp,zyc_zdr,wol,rodz_opie,mien,drog,
row.names = woj) gdzie:
krym– przestępstwa o charakterze kryminalnym,gosp– przestępstwa o charakterze gospodarczym,zyc_zdr– przestępstwa przeciwko życiu i zdrowiu,wol– przestępstwa przeciwko wolności, wolności sumienia i wyznania, wolności seksualnej i obyczjności,rodz_opie– przestępstwa przeciwko rodzinie i opiece,mien– przestępstwa przeciwko mieniu,drog– przestępstwa drogowe.
Zanim przystąpimy do analiz warto przekształcić tabelę g w tabelę kontyngencji.
Można to zrobić w następujący sposób:
g <- G[,-8]
m <- array(
c(g[,1],g[,2],g[,3],g[,4],g[,5],g[,6],g[,7]), # kolumny tabeli
dim=c(length(g[,1]),length(g[1,])), # liczba wierszy, kolumn
dimnames = list(
województwo=c(rownames(g)), # nazwy wierszy
przestępczość=c(colnames(g)))) # nazwy kolumnW pierwszej kolejności zbadamy czy występuje zależność między województwami a rodzajem przestępstwa. Zrobimy to za pomocą testu niezależności \(\chi^2\).
vcd::assocstats(m)## X^2 df P(> X^2)
## Likelihood Ratio 46183 90 0
## Pearson 50592 90 0
##
## Phi-Coefficient : NA
## Contingency Coeff.: 0.166
## Cramer's V : 0.069Wartość p-value jest równa 0. Zatem występuje pewna zależność między zmiennymi. Do oceny siły tego związku wykorzystamy współczynniki kontyngencji oraz Cramera. Wynoszą one odpowiednio: \(0,166\) i \(0,069\) czyli badana zależność nie jest zbyt wysoka.
12.2 Mapy
Gdy tabela kontyngencji jest dość sporych rozmiarów, warto liczebności w niej występujące przedstawić za pomocą różnych funkcji graficznych. Jedną z możliwości
jest wykorzystanie komendy heatmap króra rysuje tzw. “mapa ciepła”.
library("RColorBrewer")
par(mfcol=c(1,1),mar=c(4,4,1,1)+0.1,
mgp=c(3,0.6,0),las=1)
heatmap(as.matrix(g), Colv=NA, scale="column",
col= rev(brewer.pal(11,"Spectral")))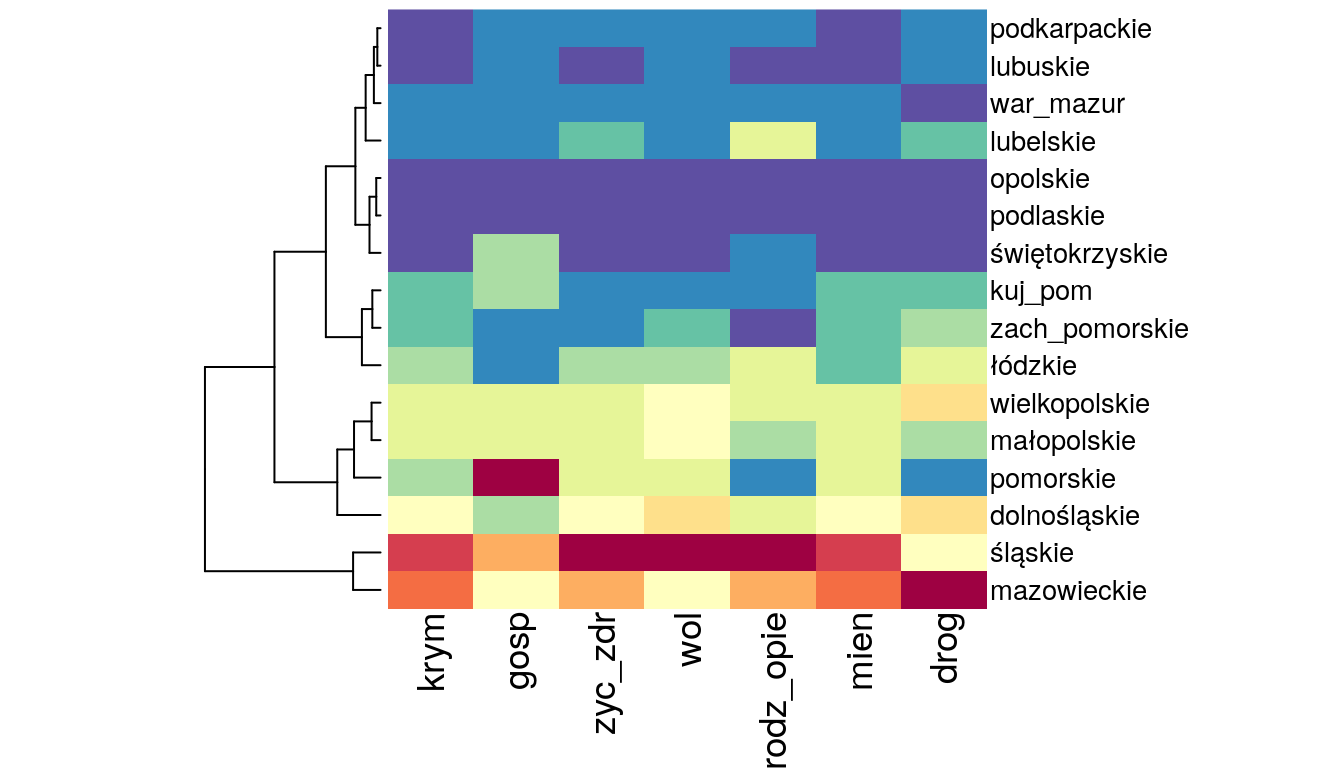
Rysunek 12.1: Mapa ciepła.
Na podstawie otrzymanej tzw. “mapy ciepła”" (rys. 12.1) możemy wyodrębnić kilka grup województw. W skład pierwszej z nich wchodzą dwa województwa: śląskie i mazowieckie. Charakteryzują się one dużymi liczebnościami przestępstw. Kolejna grupa to: wielkopolskie, małopolskie, pomorskie (duża liczeność przestępstw gospodarczych), dolnośląskie o średniej przestępczości. Ostatnią grupę stanowią głównie województwa ze wschodniej części kraju: podkarpackie, warmińsko-mazurskie, lubelskie, podlaskie, świętokrzyskie oraz lubuskie, zachodnio-pomorskie, łódzkie, kujawsko-pomorskie i opolskie. W tych województwach liczba przestępstw była najmniejsza.
heatmap(as.matrix(t(g)), Colv=NA, scale="column",
col= rev(brewer.pal(11,"Spectral")))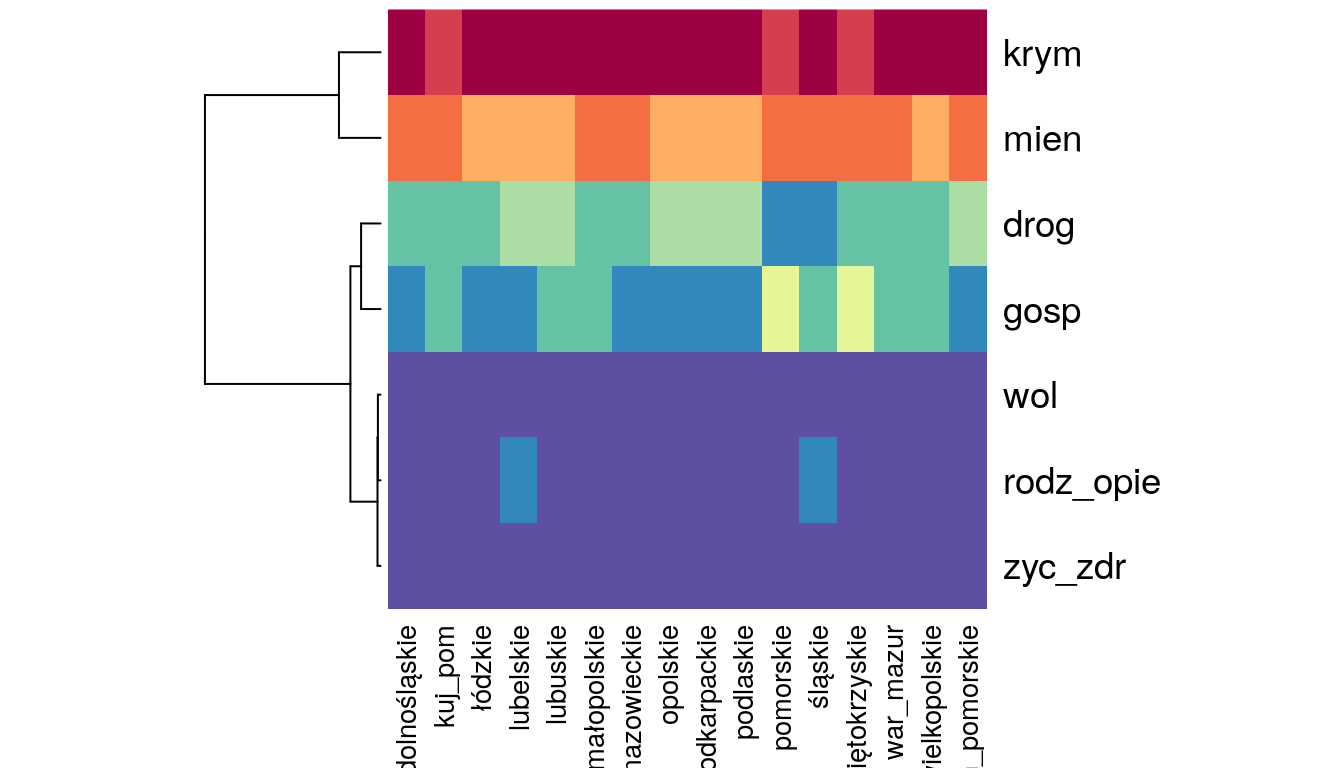
Rysunek 12.2: Mapa ciepła.
Po transformacji tabeli g i utworzeniu rys. 12.2 nasuwają się kolejne wnioski. We
wszystkich województwach przestępstwa o charakterze kryminalnym oraz przeciwko mieniu są popełniane najczęściej. Natomiast najrzadziej przestępstwa przeciwko
wolności, wolności sumienia i wyznania, wolności seksualnej i obyczjności, rodzinie i opiece a także życiu i zdrowiu.
Inną graficzną formą przedstawienia naszych danych jest mapa Polski z podziałem na województwa. Do takiej prezentacji danych (rys. 12.3 i 12.4) wykorzystamy pakiet mapoland. Dane można wizualizować na mapach także wczytując formaty plików shapefile które są dostępne pod adresem: GUGiK. Aby importować tego typu dane warto skorzystać z pakietu rgdal.
library("mapoland")
library("classInt")
library("RColorBrewer")
# dane:
przest <- as.numeric(apply(G, 1, sum))
NAM <- sapply(1:16,
function(i) paste(format(przest[i],big.mark=" "),"\n",rownames(G)[i],sep=" "))
names(NAM) <- c(2,4,10, 6,8,12,14,16,18,20,22,24,26,28,30,32) # TERYT
a <- structure(przest, names=rownames(NAM))
s <- getShape("voiv")
# kolory:
przedzialy <- 3
kolory <- brewer.pal(przedzialy,"Greens")
klasy <- classIntervals(przest, przedzialy,style="fixed",
fixedBreaks=c(0,100000,200000,300000))
tabela.kolorow <- findColours(klasy,kolory)
# rysunek:
par(mfcol=c(1,1),mar=c(0,0,0,0)+0.1,mgp=c(3,0.6,0),
bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(s, col=tabela.kolorow)
text( coordinates(s), labels=NAM, col="black",cex=1)
legend("bottomleft",
c("mniej niż 100 000","[100 000 - 200 000)","200 000 i więcej"),
fill=attr(tabela.kolorow,"palette"),cex=1,bty="n")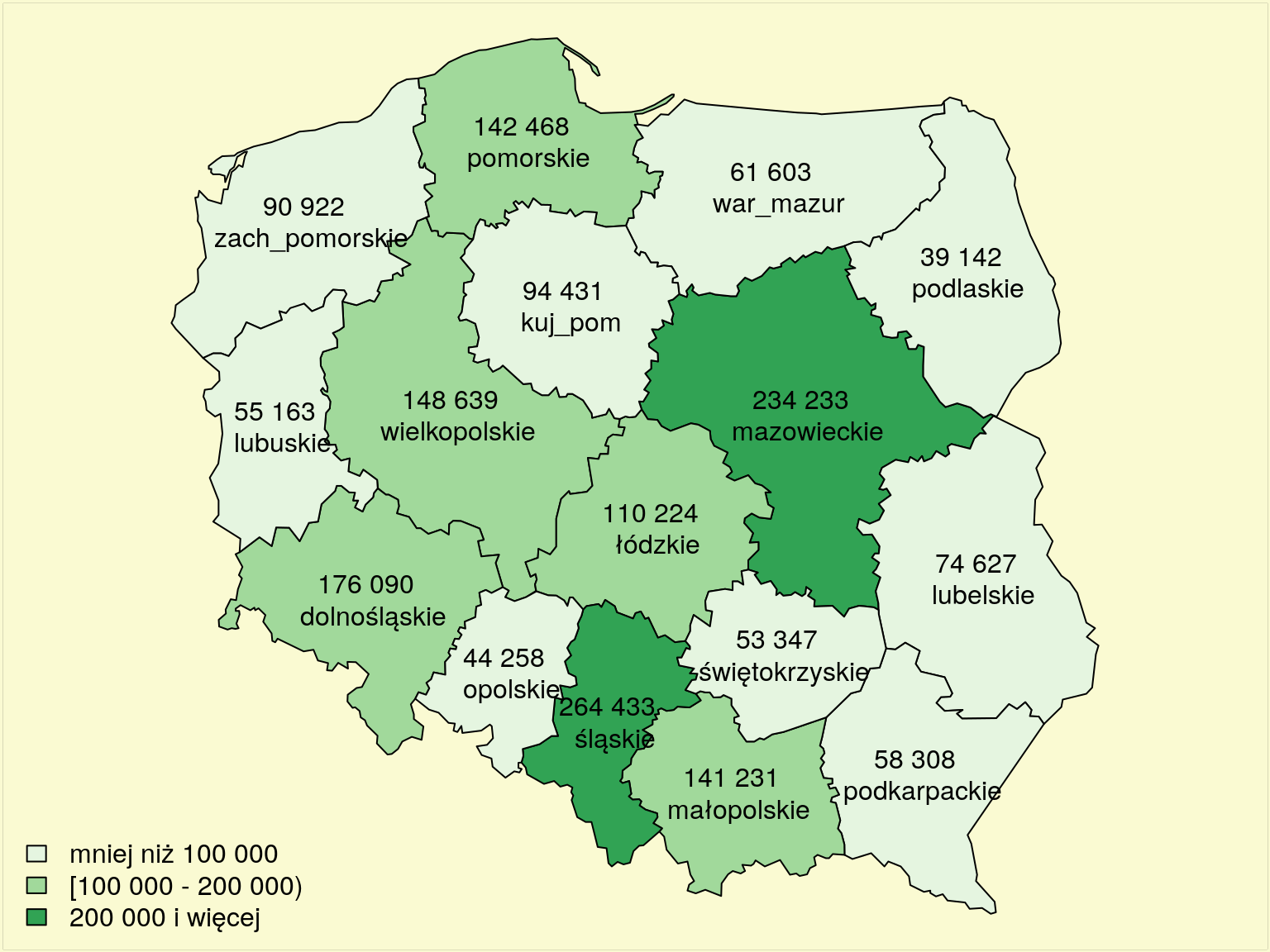
Rysunek 12.3: Liczba przestępstw w 2009 r.
# dane:
lud <- c(2876627, 2069083, 2541832, 2157202, 1010047, 3298270, 5222167, 1031097,
2101732, 1189731, 2230099, 4640725, 1270120, 1427118, 3408281, 1693198)
pw <- przest/lud # częstość przestępstw w województwach
pwL <- pw*100000
NAM <- sapply(1:16, function(i) paste(format(pw[i],digits=3),
"\n",rownames(G)[i],sep=" "))
names(NAM) <- c(2,4,10, 6,8,12,14,16,18,20,22,24,26,28,30,32) # TERYT
a <- structure(przest, names=rownames(NAM))
s <- getShape("voiv")
# kolory:
przedzialy <- 4
kolory <- brewer.pal(przedzialy,"Reds")
klasy <- classIntervals(pw, przedzialy,style="fixed",
fixedBreaks=c(0,0.03,0.04,0.05,0.06,1))
tabela.kolorow <- findColours(klasy,kolory)
# rysunek:
par(mfcol=c(1,1),mar=c(0,0,0,0)+0.1,mgp=c(3,0.6,0),
bg="lightgoldenrodyellow",las=1)
plot(1,axes=F,xlab="",ylab="",main="", col="white")
u <- par("usr")
rect(u[1], u[3], u[2], u[4], col="white")
par(new=plot)
plot(s, col=tabela.kolorow)
text( coordinates(s), labels=NAM, col="black",cex=1)
legend("bottomleft",
c("mniej niż 0.03","[0.03 - 0.04)","[0.04 - 0.05)", "[0.05 - 0.06)", "0.06 i więcej"),
fill=attr(tabela.kolorow,"palette"),cex=.8,bty="n")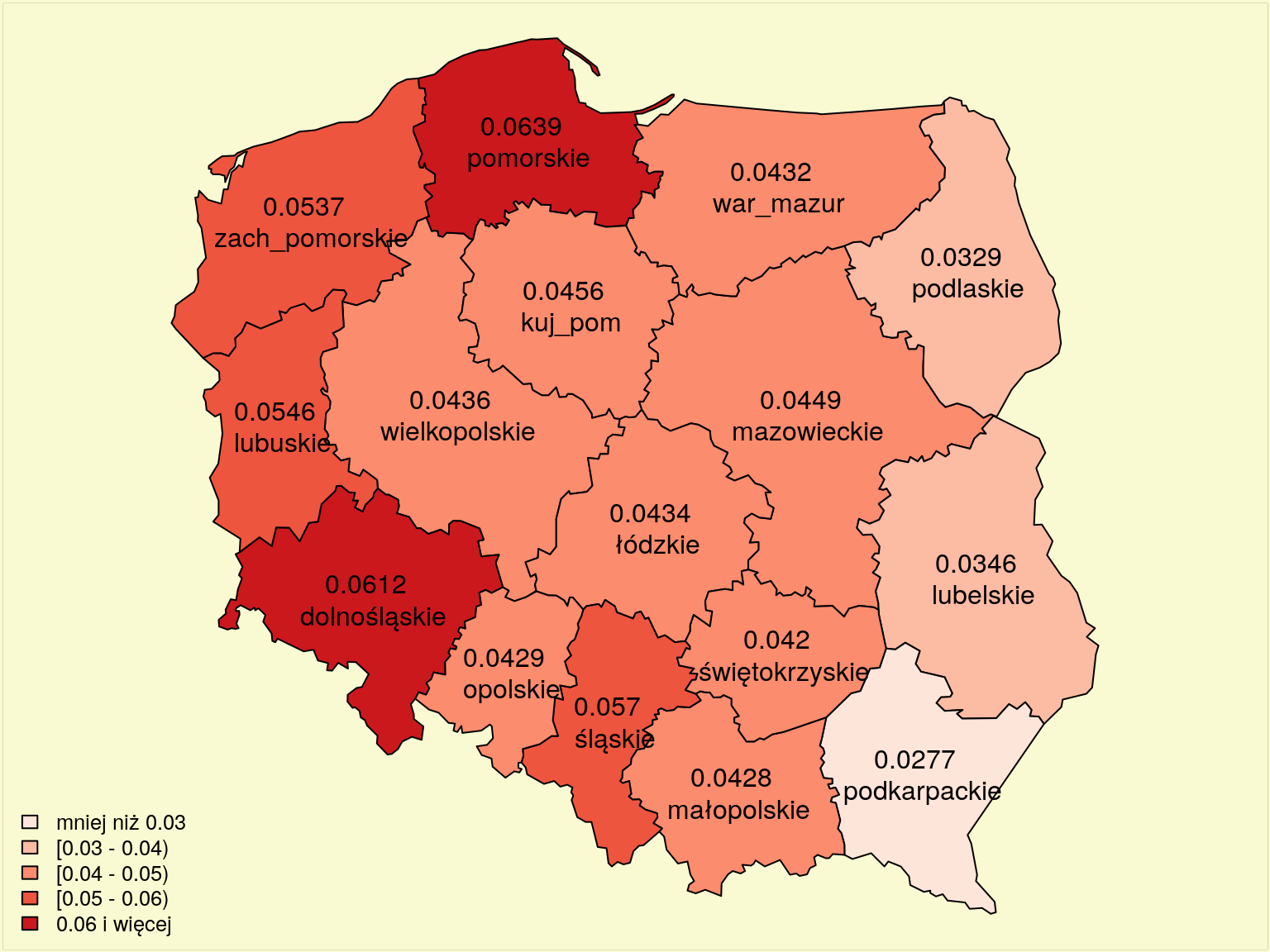
Rysunek 12.4: Częstość przestępstw w 2009 r.
Przestępstwa w przeliczeniu na jednego mieszkańca (rys. 12.4) najczęściej odnotowywano w dwóch województwach: dolnośląskim i pomorskim. Najmniej zachowań zabronionych prawem zanotowano w województwie podkarpackim.
12.3 Analiza wariancji
Analiza wariancji to kolejna metoda którą wykorzystamy w naszych badaniach.
Za pomocą komendy anova porównamy wartości średnie dla poszczególnych województw oraz kategorii przestępstw.
y <- c(g[,1],g[,2],g[,3],g[,4],g[,5],g[,6],g[,7])
woj <- rep(rownames(g),7); woj=factor(woj)
przest <- rep(colnames(g),each=16); przest=factor(przest)
anova(lm(y~woj+przest))## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## woj 15 9.9360e+09 662403078 4.0995 1.18e-05 ***
## przest 6 3.3188e+10 5531403342 34.2326 < 2.2e-16 ***
## Residuals 90 1.4542e+10 161582725
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analiza wariancji wskazuje, że śrenie liczebości czynów zabronionych dla województw (p-value = 1,18e-05) oraz ich charakteru (p-value = 2,2e-16) różnią się na poziomie istotności \(\alpha = 0,05\) (rys. 12.5).
# średnie i mediany:
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot.design(data.frame(woj,przest,y),fun=mean,col='darkred',lwd=2)
plot.design(data.frame(woj,przest,y),fun=median,col='darkred',lwd=2)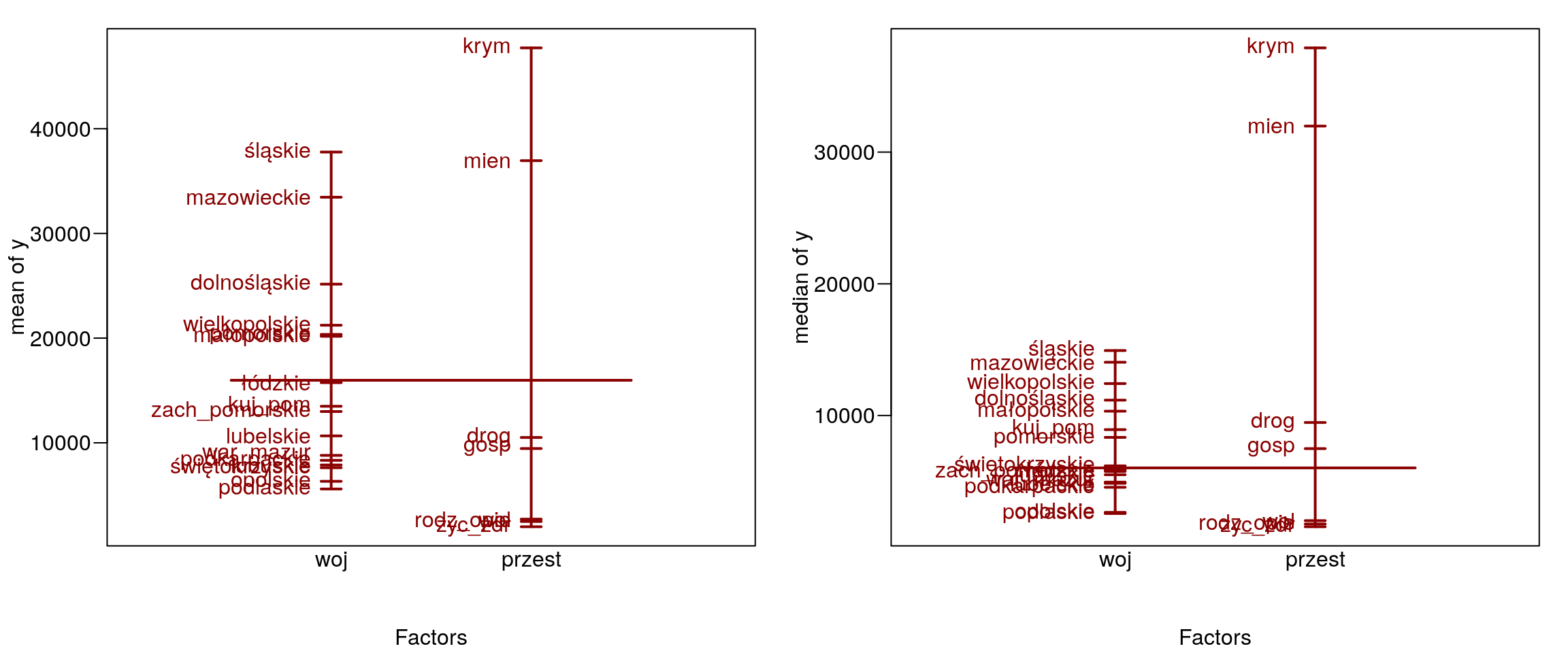
Rysunek 12.5: Średnie i mediany.
Wartości średnie dla województw są następujące:
tapply(y,woj,mean)## dolnośląskie kuj_pom lubelskie lubuskie łódzkie
## 25155.714 13490.143 10661.000 7880.429 15746.286
## małopolskie mazowieckie opolskie podkarpackie podlaskie
## 20175.857 33461.857 6322.571 8329.714 5591.714
## pomorskie śląskie świętokrzyskie war_mazur wielkopolskie
## 20352.571 37776.143 7621.000 8800.429 21234.143
## zach_pomorskie
## 12988.857Natomiast dla rodzaju przestępstwa:
tapply(y,przest,mean)## drog gosp krym mien rodz_opie wol zyc_zdr
## 10509.250 9454.062 47724.812 36953.812 2485.375 2710.875 1981.750Ponieważ średnie różnią się na poziomie istotności \(\alpha = 0,05\), możemy być zainteresowani odpowiedzią na następujące pytanie: Jak duże są różnice między badanymi wartościami w porównaiu z województwem ślaskim oraz przestępczością kryminalną. Odpowiedź na tak postawione pytanie otrzymamy wykonyjąc odpowiednią komendę:
# punkt odniesienia: województwo śląskie:
woj <- relevel(woj, ref="śląskie")
# punkt odniesienia: przestępstwa kryminalne:
przest <- relevel(przest, ref="krym")
lmtest::coeftest(lm(y~woj+przest))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 69526.7 5633.8 12.3410 < 2.2e-16 ***
## wojdolnośląskie -12620.4 6794.6 -1.8574 0.0665213 .
## wojkuj_pom -24286.0 6794.6 -3.5743 0.0005671 ***
## wojlubelskie -27115.1 6794.6 -3.9907 0.0001341 ***
## wojlubuskie -29895.7 6794.6 -4.3999 2.967e-05 ***
## wojłódzkie -22029.9 6794.6 -3.2423 0.0016638 **
## wojmałopolskie -17600.3 6794.6 -2.5903 0.0111839 *
## wojmazowieckie -4314.3 6794.6 -0.6350 0.5270663
## wojopolskie -31453.6 6794.6 -4.6292 1.229e-05 ***
## wojpodkarpackie -29446.4 6794.6 -4.3338 3.807e-05 ***
## wojpodlaskie -32184.4 6794.6 -4.7368 8.060e-06 ***
## wojpomorskie -17423.6 6794.6 -2.5643 0.0119944 *
## wojświętokrzyskie -30155.1 6794.6 -4.4381 2.566e-05 ***
## wojwar_mazur -28975.7 6794.6 -4.2645 4.933e-05 ***
## wojwielkopolskie -16542.0 6794.6 -2.4346 0.0168824 *
## wojzach_pomorskie -24787.3 6794.6 -3.6481 0.0004424 ***
## przestdrog -37215.6 4494.2 -8.2808 1.073e-12 ***
## przestgosp -38270.7 4494.2 -8.5156 3.498e-13 ***
## przestmien -10771.0 4494.2 -2.3966 0.0186146 *
## przestrodz_opie -45239.4 4494.2 -10.0662 < 2.2e-16 ***
## przestwol -45013.9 4494.2 -10.0160 2.646e-16 ***
## przestzyc_zdr -45743.1 4494.2 -10.1782 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Na podstawie powyższych obliczeń możemy sformułować kilka wniosków. Największa różnica w średnich występuje między województwem śląskim a podlaskim (rys. 12.5 i wynosi \(-32184,4\). Natomiast najmniejsza różnica jest między województwem śląskim a mazowieckim i jest równa \(-4314,3\). Jeśli porównamy wartość średnią przestępstw kryminalnych z pozostałymi to dojdziemy do wniosku, że największ różnica występuje między przestępstwami kryminalnymi i przeciwko zdrowiu i życiu a najmniejsza wynosi \(-10771\) i dotyczy przestępstw kryminalnych oraz przeciwko mieniu. Na wykresach (12.6 i 12.7) zostały zaprezentowane różnice w liczebnościach zachowań niezgodnych z prawem.
interaction.plot(woj,przest,y,col=1:7,las=1,lwd=2)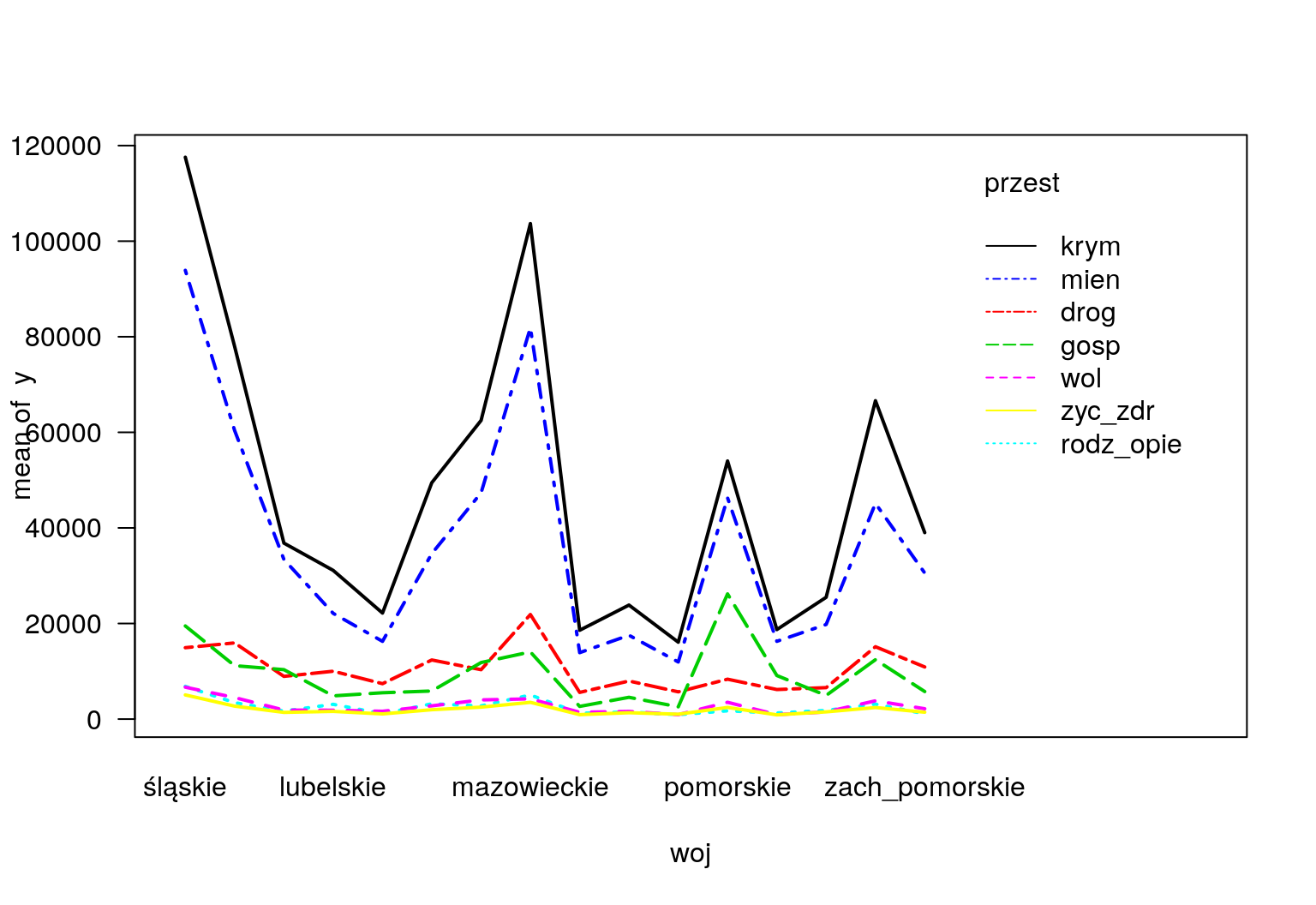
Rysunek 12.6: Rozkład liczebności.
interaction.plot(przest,woj,y,col=1:16,las=1,lwd=2)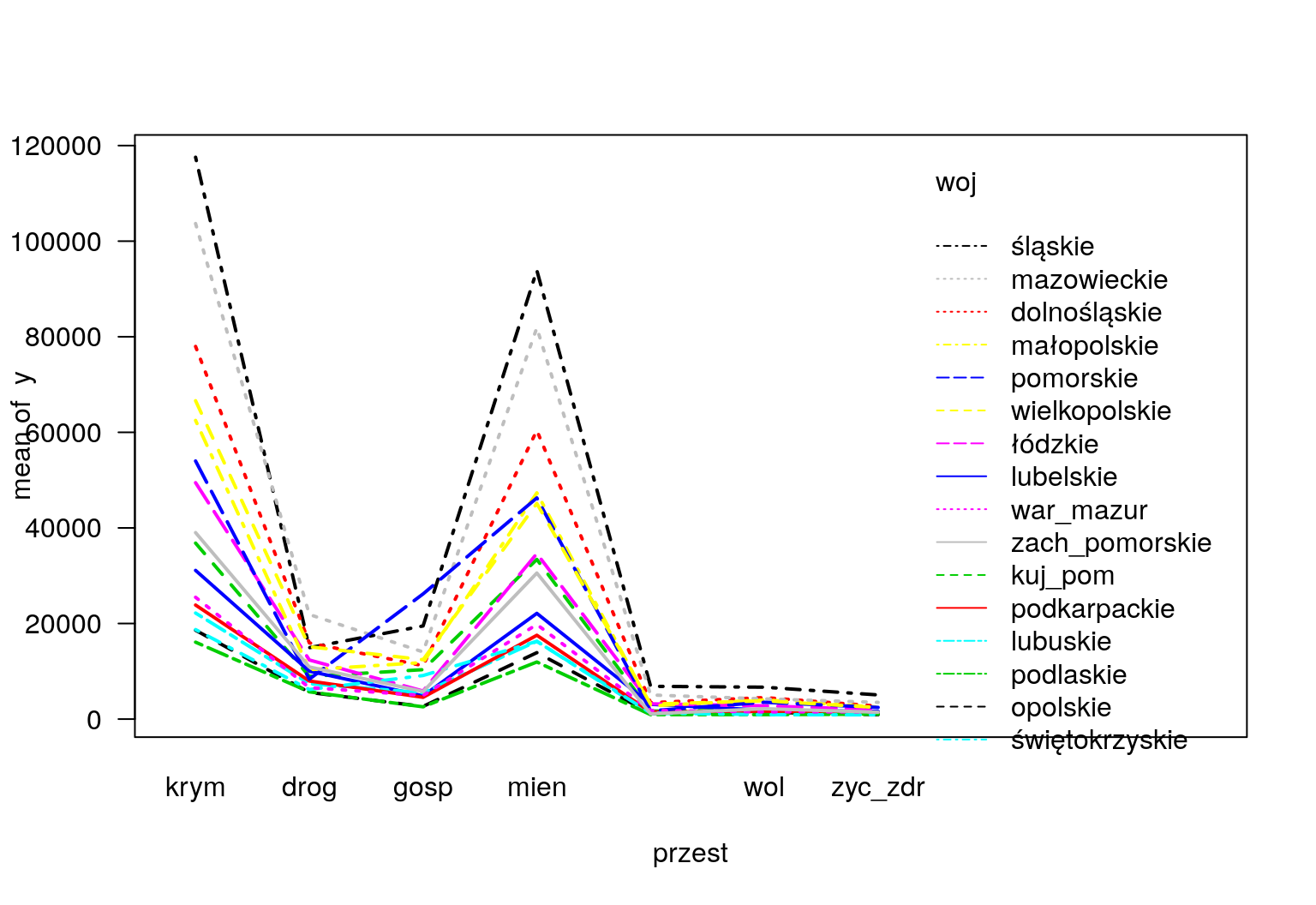
Rysunek 12.7: Rozkład liczebności.
12.4 Modele dla liczebności
Do modelowania liczebności wystąpień określonego zjawiska (np. liczba przestępstw) możemy wykorzystać model Piossona lub ujemny dwumianowy. W pierwszej kolejności zaprezentujemy model Poissona.
pois <- glm(y~woj+przest,family=poisson)
summary(pois)##
## Call:
## glm(formula = y ~ woj + przest, family = poisson)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -68.004 -8.790 -0.525 9.825 111.295
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 11.633905 0.002129 5464.68 <2e-16 ***
## wojdolnośląskie -0.406593 0.003076 -132.19 <2e-16 ***
## wojkuj_pom -1.029719 0.003791 -271.62 <2e-16 ***
## wojlubelskie -1.265086 0.004145 -305.20 <2e-16 ***
## wojlubuskie -1.567295 0.004681 -334.84 <2e-16 ***
## wojłódzkie -0.875073 0.003585 -244.07 <2e-16 ***
## wojmałopolskie -0.627191 0.003296 -190.30 <2e-16 ***
## wojmazowieckie -0.121272 0.002837 -42.74 <2e-16 ***
## wojopolskie -1.787552 0.005136 -348.06 <2e-16 ***
## wojpodkarpackie -1.511849 0.004575 -330.45 <2e-16 ***
## wojpodlaskie -1.910392 0.005416 -352.75 <2e-16 ***
## wojpomorskie -0.618470 0.003286 -188.19 <2e-16 ***
## wojświętokrzyskie -1.600770 0.004746 -337.27 <2e-16 ***
## wojwar_mazur -1.456877 0.004474 -325.65 <2e-16 ***
## wojwielkopolskie -0.576067 0.003242 -177.70 <2e-16 ***
## wojzach_pomorskie -1.067586 0.003844 -277.69 <2e-16 ***
## przestdrog -1.513196 0.002694 -561.73 <2e-16 ***
## przestgosp -1.619007 0.002814 -575.27 <2e-16 ***
## przestmien -0.255783 0.001732 -147.65 <2e-16 ***
## przestrodz_opie -2.955028 0.005144 -574.50 <2e-16 ***
## przestwol -2.868180 0.004936 -581.06 <2e-16 ***
## przestzyc_zdr -3.181471 0.005731 -555.11 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 2553250 on 111 degrees of freedom
## Residual deviance: 46183 on 90 degrees of freedom
## AIC: 47424
##
## Number of Fisher Scoring iterations: 4# Badanie istotności statystycznej całego modelu:
lmtest::lrtest(pois)## Likelihood ratio test
##
## Model 1: y ~ woj + przest
## Model 2: y ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 22 -23690
## 2 1 -1277223 -21 2507066 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Oszacowany model Poissona okazał się istotny statystycznie. Jednak założenie dotyczące równości wariancji i średniej nie zostało spełnione: \[ H_0:\;\phi=1\quad\mbox{vs.}\quad H_1:\;\phi\neq 1 \]
AER::dispersiontest(pois, alt="two.sided")##
## Dispersion test
##
## data: pois
## z = 2.8493, p-value = 0.004382
## alternative hypothesis: true dispersion is not equal to 1
## sample estimates:
## dispersion
## 451.6853Tak więc na poziomie istotności \(\alpha = 0,05\) odrzucamy hipotezę zerową, która zakłada, że dyspersja (czyli iloraz wariancji i średniej) jest równa 1. A zatem sprawdźmy czy występuje problem nadmiernego rozproszenia (wariancja jest większa od średniej): \[ H_0:\;\phi\leq1\quad\mbox{vs.}\quad H_1:\;\phi> 1 \]
AER::dispersiontest(pois)##
## Overdispersion test
##
## data: pois
## z = 2.8493, p-value = 0.002191
## alternative hypothesis: true dispersion is greater than 1
## sample estimates:
## dispersion
## 451.6853Na poziomie istotności \(\alpha = 0,05\) przymujemy hipotezę alternatywną, która zakłada, że występuje nadmierne rozproszenie (overdispersion). W takiej syuacji możemy zastosować model ujemny dwumianowy.
nb <- MASS::glm.nb(y~woj+przest); summary(nb)##
## Call:
## MASS::glm.nb(formula = y ~ woj + przest, init.theta = 21.74640825,
## link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6804 -0.5515 -0.0864 0.5432 3.9689
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 11.57767 0.09512 121.714 < 2e-16 ***
## wojdolnośląskie -0.45311 0.11477 -3.948 7.88e-05 ***
## wojkuj_pom -1.05428 0.11485 -9.180 < 2e-16 ***
## wojlubelskie -1.10428 0.11485 -9.615 < 2e-16 ***
## wojlubuskie -1.46951 0.11493 -12.786 < 2e-16 ***
## wojłódzkie -0.84128 0.11481 -7.327 2.35e-13 ***
## wojmałopolskie -0.63055 0.11479 -5.493 3.95e-08 ***
## wojmazowieckie -0.20431 0.11475 -1.780 0.074998 .
## wojopolskie -1.68246 0.11499 -14.632 < 2e-16 ***
## wojpodkarpackie -1.39677 0.11491 -12.155 < 2e-16 ***
## wojpodlaskie -1.81041 0.11503 -15.739 < 2e-16 ***
## wojpomorskie -0.57400 0.11478 -5.001 5.71e-07 ***
## wojświętokrzyskie -1.49467 0.11494 -13.004 < 2e-16 ***
## wojwar_mazur -1.34852 0.11490 -11.736 < 2e-16 ***
## wojwielkopolskie -0.56953 0.11478 -4.962 6.98e-07 ***
## wojzach_pomorskie -1.13722 0.11486 -9.901 < 2e-16 ***
## przestdrog -1.38273 0.07587 -18.224 < 2e-16 ***
## przestgosp -1.57685 0.07588 -20.780 < 2e-16 ***
## przestmien -0.25984 0.07584 -3.426 0.000612 ***
## przestrodz_opie -2.91336 0.07604 -38.312 < 2e-16 ***
## przestwol -2.83470 0.07603 -37.285 < 2e-16 ***
## przestzyc_zdr -3.11696 0.07609 -40.963 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(21.7464) family taken to be 1)
##
## Null deviance: 4061.80 on 111 degrees of freedom
## Residual deviance: 112.78 on 90 degrees of freedom
## AIC: 2002
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 21.75
## Std. Err.: 2.90
##
## 2 x log-likelihood: -1955.994Znając wartość parametru rozproszenia \(\theta = 21,7464\) oraz jego błąd standardowy \(\sigma_\theta = 2,90\) możemy ocenić jego istotność statystyczną badając następujące hipotezy: \[ H_0:\;\theta=0\quad\mbox{vs.}\quad H_1:\;\theta\neq 0 \]
pnorm(2*(1-abs(21.7464/2.9)))## [1] 6.318995e-39# Badanie istotności statystycznej całego modelu:
lmtest::lrtest(nb)## Likelihood ratio test
##
## Model 1: y ~ woj + przest
## Model 2: y ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 23 -978.0
## 2 2 -1191.5 -21 426.95 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Model ujemny dwumianowy możemy estymować także z wykorzystaniem funkcji
glm oraz opcji MASS::negative.binomial:
th <- MASS::theta.ml(nb,fitted(nb))
th## [1] 21.74641
## attr(,"SE")
## [1] 2.899898# Estymacja modelu ujemnego dwumianowego:
n <- glm(y~woj+przest, family=MASS::negative.binomial(th))
# Porównanie modelu Poissona oraz ujemnego dwumianowego:
lmtest::lrtest(pois,nb)## Likelihood ratio test
##
## Model 1: y ~ woj + przest
## Model 2: y ~ woj + przest
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 22 -23690
## 2 23 -978 1 45424 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Przeprowadzony test ilorazu wiarygodności - lmtest::lrtest wykazał, że model
ujemny dwumianowy - nb ma znacznie wyższy logarytm funkcji wiarygodności. Zatem na podstawie modelu ujemnego dwumianowego należy stwierdzić, że we wszystkich województwach odnotowano mniejszą liczbę przestępstw (ujemne parametry)
niż w województwie śląskim. Taka sama sytuacja występuje gdy porównamy wszystkie rodzaje czynów zabronionych z przestępstwami o charakterze kryminalnym. Aby
dowiedzieć się jak duże są to różnice należy obliczyć ilorazy wiarygodności.
ORpois1 <- round((exp(coef(pois))-1)*100,4)
ORnb <- round((exp(coef(nb))-1)*100,4)
cbind(ORpois1,ORnb)## ORpois1 ORnb
## (Intercept) 11285915.3797 10668768.3273
## wojdolnośląskie -33.4085 -36.4350
## wojkuj_pom -64.2893 -65.1558
## wojlubelskie -71.7785 -66.8550
## wojlubuskie -79.1391 -76.9962
## wojłódzkie -58.3169 -56.8840
## wojmałopolskie -46.5910 -46.7701
## wojmazowieckie -11.4207 -18.4792
## wojopolskie -83.2631 -81.4084
## wojpodkarpackie -77.9498 -75.2606
## wojpodlaskie -85.1978 -83.6413
## wojpomorskie -46.1232 -43.6730
## wojświętokrzyskie -79.8259 -77.5678
## wojwar_mazur -76.7037 -74.0376
## wojwielkopolskie -43.7895 -43.4210
## wojzach_pomorskie -65.6162 -67.9290
## przestdrog -77.9795 -74.9108
## przestgosp -80.1905 -79.3375
## przestmien -22.5690 -22.8826
## przestrodz_opie -94.7923 -94.5707
## przestwol -94.3198 -94.1264
## przestzyc_zdr -95.8475 -95.5708Interpretacja otrzymanych ilorazów wiarygodności na podstawie modelu ujemnego dwumianowego jest następująca:
Aż o \(83,6\%\) mniej popełniono przestępstw w województwie podlaskim niż w województwie śląskim.
W województwie mazowieckim popełniono tylko o \(18,5\%\) mniej przestępstw niż w województwie ślaskim.
Najmniejsze różnice w liczebności przestępstw w porównaniu z województwem śląskim zanotowano w następujących województwach: dolnośląskim (\(-36,4\%\)), małopolskim (\(-46,8\%\)), mazowieckim (\(-18,5\%\)), pomorskim (\(-43,7\%\)) i wielkopolskim (\(-43,4\%\)).
Z kolei największe różnice zanotowano w województwach: kujawsko-pomorskim (\(-65,2\%\)), lubelskim (\(-66,9\%\)), lubuskim (\(-77\%\)), łódzkim (\(-56,9\%\)), opolskim (\(-81,4\%\)), podkarpackim (\(-75,3\%\)), podlaskim (\(-83,6\%\)), świętokrzyskim (\(-77,6\%\)), warmińsko-mazurskim (\(-74\%\)) oraz zachodnio-pomorskim (\(-68\%\)).
Przestępstw przeciwko mieniu popełniono tylko o \(22,9\%\) mniej niż kryminalnych.
Przestępstw o charakterze gospodarczym popełniono o \(79,3\%\) mniej niż kryminalnych, natomiast w przypadku pozostałych było ich mniej o ponad \(90\%\).
12.5 Modele dla częstości
Do modelowania częstości wystąpień określonego zjawiska (liczba przestępstw na jednego mieszkańca) wykorzystamy modele Poisona oraz modele logitowe. W pierwszej
kolejności zostanie przedstawiony model Poissona w którym zostanie wykorzystana
funkcja offset.
L <- rep(lud,7) # liczebności
W <- y/L # częstości
pois1 <- glm(y~woj+przest, family=poisson,offset=log(L)) # model pois1
summary(pois1)##
## Call:
## glm(formula = y ~ woj + przest, family = poisson, offset = log(L))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -68.004 -8.790 -0.525 9.825 111.295
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.716476 0.002129 -1745.704 <2e-16 ***
## wojdolnośląskie 0.071659 0.003076 23.298 <2e-16 ***
## wojkuj_pom -0.221953 0.003791 -58.548 <2e-16 ***
## wojlubelskie -0.499027 0.004145 -120.390 <2e-16 ***
## wojlubuskie -0.042422 0.004681 -9.063 <2e-16 ***
## wojłódzkie -0.273088 0.003585 -76.170 <2e-16 ***
## wojmałopolskie -0.285719 0.003296 -86.692 <2e-16 ***
## wojmazowieckie -0.239313 0.002837 -84.342 <2e-16 ***
## wojopolskie -0.283304 0.005136 -55.163 <2e-16 ***
## wojpodkarpackie -0.719740 0.004575 -157.315 <2e-16 ***
## wojpodlaskie -0.549248 0.005416 -101.418 <2e-16 ***
## wojpomorskie 0.114354 0.003286 34.796 <2e-16 ***
## wojświętokrzyskie -0.305011 0.004746 -64.264 <2e-16 ***
## wojwar_mazur -0.277664 0.004474 -62.065 <2e-16 ***
## wojwielkopolskie -0.267405 0.003242 -82.486 <2e-16 ***
## wojzach_pomorskie -0.059334 0.003844 -15.434 <2e-16 ***
## przestdrog -1.513196 0.002694 -561.726 <2e-16 ***
## przestgosp -1.619007 0.002814 -575.271 <2e-16 ***
## przestmien -0.255783 0.001732 -147.654 <2e-16 ***
## przestrodz_opie -2.955028 0.005144 -574.505 <2e-16 ***
## przestwol -2.868180 0.004936 -581.064 <2e-16 ***
## przestzyc_zdr -3.181471 0.005731 -555.108 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 2048950 on 111 degrees of freedom
## Residual deviance: 46183 on 90 degrees of freedom
## AIC: 47424
##
## Number of Fisher Scoring iterations: 4W celu poprawnego oszacowania istotności poszczególnych zmiennych (występuje problem nadmiernego rozproszenia) skorzystamy z takiego modelu który uwzględni to zjawisko.
# model rpois1 z odpornymi błędami standardowymi:
rpois1 <- glm(y~woj+przest, family=quasipoisson,offset=log(L))
lmtest::coeftest(rpois1)##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.716476 0.050476 -73.6289 < 2.2e-16 ***
## wojdolnośląskie 0.071659 0.072926 0.9826 0.3257866
## wojkuj_pom -0.221953 0.089882 -2.4694 0.0135343 *
## wojlubelskie -0.499027 0.098278 -5.0777 3.820e-07 ***
## wojlubuskie -0.042422 0.110979 -0.3823 0.7022759
## wojłódzkie -0.273088 0.085005 -3.2126 0.0013153 **
## wojmałopolskie -0.285719 0.078142 -3.6564 0.0002558 ***
## wojmazowieckie -0.239313 0.067274 -3.5573 0.0003747 ***
## wojopolskie -0.283304 0.121767 -2.3266 0.0199862 *
## wojpodkarpackie -0.719740 0.108474 -6.6351 3.243e-11 ***
## wojpodlaskie -0.549248 0.128403 -4.2775 1.890e-05 ***
## wojpomorskie 0.114354 0.077920 1.4676 0.1422180
## wojświętokrzyskie -0.305011 0.112531 -2.7105 0.0067190 **
## wojwar_mazur -0.277664 0.106071 -2.6177 0.0088519 **
## wojwielkopolskie -0.267405 0.076862 -3.4790 0.0005032 ***
## wojzach_pomorskie -0.059334 0.091151 -0.6509 0.5150809
## przestdrog -1.513196 0.063869 -23.6920 < 2.2e-16 ***
## przestgosp -1.619007 0.066726 -24.2634 < 2.2e-16 ***
## przestmien -0.255783 0.041072 -6.2276 4.735e-10 ***
## przestrodz_opie -2.955028 0.121952 -24.2310 < 2.2e-16 ***
## przestwol -2.868180 0.117032 -24.5077 < 2.2e-16 ***
## przestzyc_zdr -3.181471 0.135885 -23.4129 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Możemy także zastosować odporne błędy standardowe sandwich w modelu pois1
które są dostępne w bibliotece sandwich.
# model pois1 z odpornymi błędami standardowymi sandwich:
lmtest::coeftest(pois1,vcov=sandwich::sandwich)##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.716476 0.047110 -78.8886 < 2.2e-16 ***
## wojdolnośląskie 0.071659 0.057827 1.2392 0.215273
## wojkuj_pom -0.221953 0.070951 -3.1282 0.001759 **
## wojlubelskie -0.499027 0.078081 -6.3911 1.647e-10 ***
## wojlubuskie -0.042422 0.078925 -0.5375 0.590926
## wojłódzkie -0.273088 0.067556 -4.0424 5.291e-05 ***
## wojmałopolskie -0.285719 0.056460 -5.0606 4.180e-07 ***
## wojmazowieckie -0.239313 0.061044 -3.9203 8.843e-05 ***
## wojopolskie -0.283304 0.067212 -4.2151 2.497e-05 ***
## wojpodkarpackie -0.719740 0.074557 -9.6535 < 2.2e-16 ***
## wojpodlaskie -0.549248 0.080313 -6.8389 7.983e-12 ***
## wojpomorskie 0.114354 0.126435 0.9044 0.365758
## wojświętokrzyskie -0.305011 0.129681 -2.3520 0.018673 *
## wojwar_mazur -0.277664 0.054721 -5.0742 3.892e-07 ***
## wojwielkopolskie -0.267405 0.060906 -4.3905 1.131e-05 ***
## wojzach_pomorskie -0.059334 0.061038 -0.9721 0.331007
## przestdrog -1.513196 0.079554 -19.0210 < 2.2e-16 ***
## przestgosp -1.619007 0.116016 -13.9550 < 2.2e-16 ***
## przestmien -0.255783 0.023665 -10.8087 < 2.2e-16 ***
## przestrodz_opie -2.955028 0.070197 -42.0960 < 2.2e-16 ***
## przestwol -2.868180 0.044015 -65.1635 < 2.2e-16 ***
## przestzyc_zdr -3.181471 0.040157 -79.2255 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Jak można zauważyć model pois1 nie oszacował poprawnie wszystkich błędów standardowych poszczególnych zmiennych. Natomiast model rpois1 (który uwzględnił
problem nadmiernego rozproszenia) wykazał kilka zmiennych które nie są statystycznie istotne.
Kolejną grupą modeli które przedstawimy to modele logitowe.
# model logit1:
logit1 <- glm(cbind(y,L-y)~woj+przest, family=binomial)
summary(logit1)##
## Call:
## glm(formula = cbind(y, L - y) ~ woj + przest, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -68.423 -8.783 -0.411 9.951 111.262
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.692865 0.002150 -1717.792 <2e-16 ***
## wojdolnośląskie 0.072989 0.003104 23.511 <2e-16 ***
## wojkuj_pom -0.225510 0.003820 -59.038 <2e-16 ***
## wojlubelskie -0.506041 0.004171 -121.334 <2e-16 ***
## wojlubuskie -0.043165 0.004721 -9.143 <2e-16 ***
## wojłódzkie -0.277357 0.003612 -76.792 <2e-16 ***
## wojmałopolskie -0.290159 0.003320 -87.387 <2e-16 ***
## wojmazowieckie -0.243116 0.002860 -85.011 <2e-16 ***
## wojopolskie -0.287712 0.005172 -55.631 <2e-16 ***
## wojpodkarpackie -0.728895 0.004599 -158.499 <2e-16 ***
## wojpodlaskie -0.556792 0.005446 -102.237 <2e-16 ***
## wojpomorskie 0.116523 0.003318 35.118 <2e-16 ***
## wojświętokrzyskie -0.309707 0.004779 -64.803 <2e-16 ***
## wojwar_mazur -0.281995 0.004506 -62.586 <2e-16 ***
## wojwielkopolskie -0.271597 0.003266 -83.150 <2e-16 ***
## wojzach_pomorskie -0.060365 0.003877 -15.569 <2e-16 ***
## przestdrog -1.529639 0.002704 -565.681 <2e-16 ***
## przestgosp -1.635913 0.002824 -579.262 <2e-16 ***
## przestmien -0.260568 0.001748 -149.044 <2e-16 ***
## przestrodz_opie -2.974984 0.005149 -577.783 <2e-16 ***
## przestwol -2.888038 0.004942 -584.426 <2e-16 ***
## przestzyc_zdr -3.201647 0.005736 -558.160 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2064429 on 111 degrees of freedom
## Residual deviance: 46562 on 90 degrees of freedom
## AIC: 47802
##
## Number of Fisher Scoring iterations: 4Podobnie jak w przypadku modelu pois1 model logit1 wskazuje, że wszystkie
zmienne są istotne. Jednak gdy wykorzystamy odporne błędy standardowe (logit2)
jak w przypadku modelu rpois1 niektóre z nich okażą się nieistotne statystycznie.
# model logit2:
logit2 <- glm(W~woj+przest, family=quasibinomial)
summary(logit2)##
## Call:
## glm(formula = W ~ woj + przest, family = quasibinomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.038182 -0.006241 -0.000791 0.006851 0.069641
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.71320 0.07066 -52.551 < 2e-16 ***
## wojdolnośląskie 0.07295 0.09326 0.782 0.43615
## wojkuj_pom -0.22541 0.10052 -2.243 0.02738 *
## wojlubelskie -0.50584 0.10894 -4.643 1.16e-05 ***
## wojlubuskie -0.04314 0.09589 -0.450 0.65386
## wojłódzkie -0.27724 0.10195 -2.719 0.00785 **
## wojmałopolskie -0.29003 0.10231 -2.835 0.00566 **
## wojmazowieckie -0.24301 0.10100 -2.406 0.01817 *
## wojopolskie -0.28759 0.10224 -2.813 0.00603 **
## wojpodkarpackie -0.72864 0.11691 -6.233 1.45e-08 ***
## wojpodlaskie -0.55658 0.11065 -5.030 2.49e-06 ***
## wojpomorskie 0.11646 0.09234 1.261 0.21047
## wojświętokrzyskie -0.30957 0.10287 -3.009 0.00340 **
## wojwar_mazur -0.28187 0.10208 -2.761 0.00698 **
## wojwielkopolskie -0.27148 0.10179 -2.667 0.00907 **
## wojzach_pomorskie -0.06034 0.09630 -0.627 0.53257
## przestdrog -1.42112 0.06483 -21.922 < 2e-16 ***
## przestgosp -1.55866 0.06851 -22.750 < 2e-16 ***
## przestmien -0.25994 0.04375 -5.941 5.26e-08 ***
## przestrodz_opie -2.95441 0.12770 -23.135 < 2e-16 ***
## przestwol -2.84778 0.12144 -23.451 < 2e-16 ***
## przestzyc_zdr -3.14558 0.13986 -22.491 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasibinomial family taken to be 0.0002521464)
##
## Null deviance: 0.819052 on 111 degrees of freedom
## Residual deviance: 0.021215 on 90 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 10Tak samo jak w przypadku modelu pois1 wykorzystamy odporne błędy standardowe
sandwich w modelu logit1.
# model logit1 z odpornymi błędami standardowymi sandwich:
lmtest::coeftest(logit1, vcov=sandwich::sandwich)##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.692865 0.048364 -76.3552 < 2.2e-16 ***
## wojdolnośląskie 0.072989 0.059493 1.2268 0.219882
## wojkuj_pom -0.225510 0.072412 -3.1143 0.001844 **
## wojlubelskie -0.506041 0.079608 -6.3567 2.061e-10 ***
## wojlubuskie -0.043165 0.080315 -0.5374 0.590963
## wojłódzkie -0.277357 0.068777 -4.0327 5.515e-05 ***
## wojmałopolskie -0.290159 0.057562 -5.0408 4.636e-07 ***
## wojmazowieckie -0.243116 0.062228 -3.9068 9.351e-05 ***
## wojopolskie -0.287712 0.068587 -4.1949 2.730e-05 ***
## wojpodkarpackie -0.728895 0.076269 -9.5569 < 2.2e-16 ***
## wojpodlaskie -0.556792 0.081916 -6.7971 1.068e-11 ***
## wojpomorskie 0.116523 0.128614 0.9060 0.364943
## wojświętokrzyskie -0.309707 0.131930 -2.3475 0.018900 *
## wojwar_mazur -0.281995 0.056052 -5.0310 4.880e-07 ***
## wojwielkopolskie -0.271597 0.062104 -4.3733 1.224e-05 ***
## wojzach_pomorskie -0.060365 0.062394 -0.9675 0.333310
## przestdrog -1.529639 0.080318 -19.0448 < 2.2e-16 ***
## przestgosp -1.635913 0.116301 -14.0663 < 2.2e-16 ***
## przestmien -0.260568 0.024119 -10.8036 < 2.2e-16 ***
## przestrodz_opie -2.974984 0.070596 -42.1412 < 2.2e-16 ***
## przestwol -2.888038 0.044042 -65.5740 < 2.2e-16 ***
## przestzyc_zdr -3.201647 0.040398 -79.2522 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wyznaczymy teraz ilorazy wiarygodności dla modeli pois1, logit1 i logit2.
ORpois1 <- round((exp(coef(pois1))-1)*100,4)
ORlogit1 <- round((exp(coef(logit1))-1)*100,4)
ORlogit2 <- round((exp(coef(logit2))-1)*100,4)
cbind(ORpois1,ORlogit1,ORlogit2)## ORpois1 ORlogit1 ORlogit2
## (Intercept) -97.5680 -97.5099 -97.5601
## wojdolnośląskie 7.4289 7.5719 7.5678
## wojkuj_pom -19.9047 -20.1891 -20.1811
## wojlubelskie -39.2879 -39.7122 -39.7002
## wojlubuskie -4.1535 -4.2246 -4.2226
## wojłódzkie -23.8974 -24.2216 -24.2125
## wojmałopolskie -24.8526 -25.1855 -25.1761
## wojmazowieckie -21.2832 -21.5820 -21.5735
## wojopolskie -24.6710 -25.0023 -24.9929
## wojpodkarpackie -51.3121 -51.7558 -51.7433
## wojpodlaskie -42.2616 -42.6956 -42.6833
## wojpomorskie 12.1149 12.3583 12.3514
## wojświętokrzyskie -26.2885 -26.6338 -26.6241
## wojwar_mazur -24.2449 -24.5723 -24.5630
## wojwielkopolskie -23.4637 -23.7839 -23.7748
## wojzach_pomorskie -5.7608 -5.8579 -5.8551
## przestdrog -77.9795 -78.3386 -75.8557
## przestgosp -80.1905 -80.5226 -78.9582
## przestmien -22.5690 -22.9386 -22.8899
## przestrodz_opie -94.7923 -94.8952 -94.7891
## przestwol -94.3198 -94.4315 -94.2027
## przestzyc_zdr -95.8475 -95.9305 -95.6958Wnioski (na podstawie modelu logit2) dotyczące ilości przestępstw przypadających
na jednego mieszkańca są następujące:
Liczba przestępstw przypadająca na jednego mieszkańca województwa pomorskiego była większa o \(12,4\%\) niż w województwie śląskim. Natomiast najmniejsza (\(-51,7\%\)) w województwie podkarpackim.
Liczba przestępstw przeciwko mieniu przypadająca na jednego mieszkańca była o \(22,9\%\) mniejsza niż liczba przestępstw kryminalnych. Z kolei liczba przestępstw przeciwko życiu i zdrowiu była aż o \(95,7\%\) mniejsza niż liczba przestępstw kryminalnych w przeliczeniu na jednego mieszkańca.