Rozdział 9 Przykład badania rozkładu stopy zwrotu z akcji

9.1 Wprowadzenie

W tym opracowaniu będziemy analizować dzienne stopy zwrotu z akcji spółki PKOBP, która wchodzi w skład indeksu giełdowego WIG20. Indeks WIG20 to portfel akcji dwudziestu największych i najbardziej płynnych spółek notowanych na GPW w Warszawie. Jego skład jest ustalany po ostatniej sesji w styczniu (korekta roczna), kwietniu, lipcu i październiku (korekty kwartalne). Akutalny stan portfela WIG20 przedstawia poniższy wykres (rys. 9.1).

spolki1 <- c(15.00,13.06,11.44,8.95,8.24,8.17,7.17,3.98,3.94,3.00,2.40,
             2.21,2.20,1.90,1.87,1.76,1.43,1.26,1.21,0.82)
val <- c('15.00%','13.06%','11.44%','8.95%','8.24%','8.17%','7.17%','3.98%','3.94%','3.00%',
         '2.40%','2.21%','2.20%','1.90%','1.87%','1.76%','1.43%','1.26%','1.21%','0.82%')
nam <- c('PKOBP','PEKAO','KGHM','PZU','PGE','PKNORLEN','TPSA','TAURONPE','PGNIG',
         'BZWBK','BRE','ASSECOPOL','GETIN','GTC','CEZ','TVN','PBG','POLIMEXMS',
         'LOTOS','CYFRPLSAT')
par(mar=c(4,6,1,1)+0.1, mgp=c(3,0.6,0),las=1)
b <- barplot(spolki1, names.arg=nam, horiz=TRUE,xlim=c(0,18))
text(spolki1, b, labels=val, pos=4)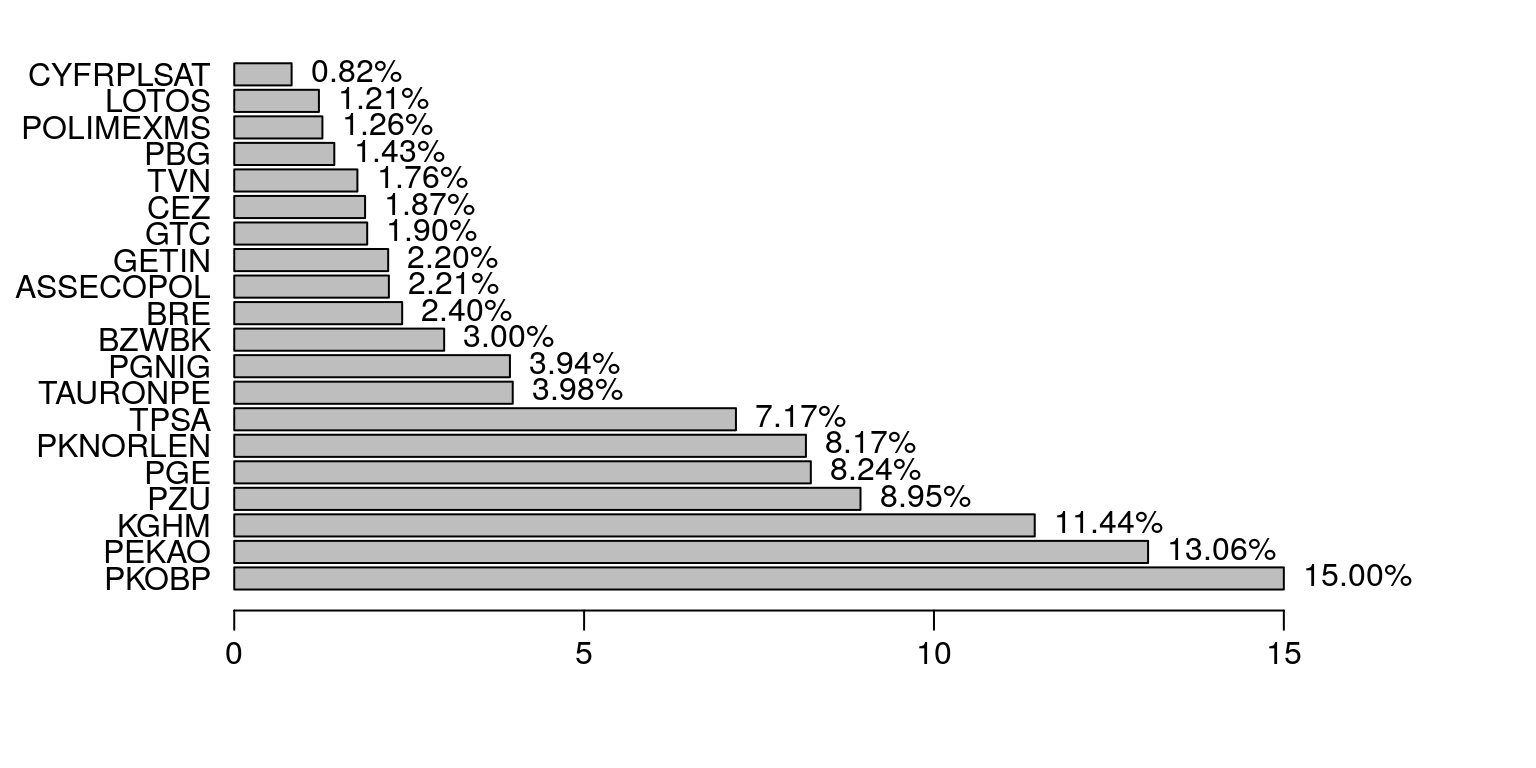
Struktura indeksu WIG20 -- stan na 17 grudnia 2010 r.

Rysunek 9.1: Struktura indeksu WIG20 – stan na 17 grudnia 2010 r.

9.2 Statystyki opisowe

Do naszych analiz zostanie wykorzystana stopa zwrotu spółki PKOBP, która ma największy udział w strukturze portfela WIG20 (rys. 9.1). Dane dotyczące notowań na warszawskiej giełdzie papierów wartościowych są dostępne w internecie. Przykładowo, po kliknięciu w odnośnik PKOBP zostaniemy przekierowani do serwisu internetowego z którego można pobrać interesujące nas dane. W kolejnym kroku można samodzielnie obliczyć logarytmiczne stopy zwrotu według wzoru: \[\begin{equation} z=\ln(Close)-\ln(Open)=\ln\left(\frac{Close}{Open}\right) \tag{9.1} \end{equation}\] gdzie: \(Close\) to cena zamknięcia oraz \(Open\) to cena otwarcia.

Innym rozwiązaniem jest pobranie już przetworzonego zestawu danych:

t <- read.csv("https://raw.githubusercontent.com/krzysiektr/datacsv/master/pkobp.csv")
head(t, 3)
##         Data Otwarcie Zamkniecie  Maks   Min Obrot_mln_zl           z
## 1 2004-11-10    14.34      15.14 15.20 14.34      2780.40 0.054287413
## 2 2004-11-12    15.14      15.26 15.94 15.14      1049.56 0.007894778
## 3 2004-11-15    15.14      15.20 15.26 14.89       425.14 0.003955180
par(mfcol=c(2,1),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(as.Date(t$Data),t$Zamkniecie,type="l",main="cena zamknięcia")
plot(as.Date(t$Data),t$z,type="l",main="stopa zwrotu")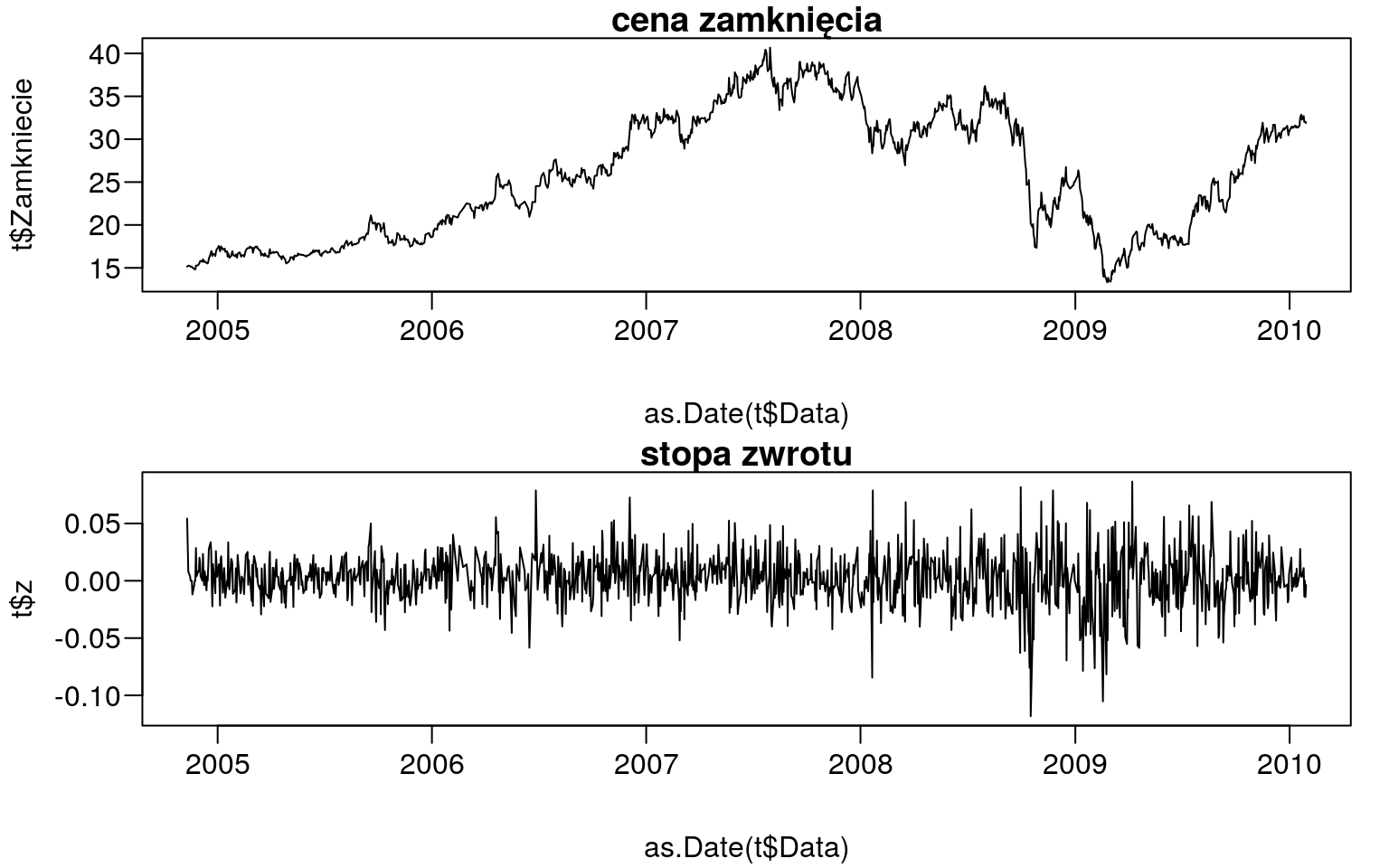
Stopy zwrotu i ceny zamknięcia od 10.11.2004 r. do 29.01.2010 r.

Rysunek 9.2: Stopy zwrotu i ceny zamknięcia od 10.11.2004 r. do 29.01.2010 r.

Poniżej obliczymy m.in. miary położenia tzn. średnią, medianę oraz kwartyle.

z <- t$z
summary(z)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -0.118224 -0.010002  0.001767  0.002169  0.014393  0.086565

a także odchylenie standardowe według wzoru: \[\begin{equation} s=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2} \tag{9.2} \end{equation}\]

sd(z)
## [1] 0.02225315

Z powyższych obliczeń wynika, że średnia stopa zwrotu w badanym okresie wyniosła \(0,22\%\), wartość maksymalna \(8,66\%\) a minimalna \(-11,82\%\). Natomiast w wypadku \(25\%\) sesji stopy zwrotu były mniejsze niż \(-0,01\%\), podczas \(50\%\) sesji wartości były mniejsze niż \(0,18\%\). Z kolei w przypadku \(75\%\) sesji zysk z akcji był mniejszy niż \(1,44\%\), a w przypadku pozostałych 25% sesji zysk był większy niż \(1,44\%\) (rys. 9.3).

Przy omawianiu różnych statystyk opisowych wato także wspomnieć o funkcji quantile. Za jej pomocą mamy możliwość obliczenia wartość dowolnego kwantyla wykorzystując jedną z dziewięciu dostępnych metod. W tym opracowaniu zaprezentujemy sposób obliczania kwantyli za pomocą metody siódmej. W pierwszym kroku uporządkujemy nasz wektor danych w sposób rosnący:

sz <- sort(z) # wektor danych uporządkowany rosnąco

Następnie wyznaczymy numer kwantyla \(Q = 80\%\) według wzoru: \[\begin{equation} h=(n-1)\cdot Q+1 \tag{9.3} \end{equation}\]

h <- (length(z)-1)*0.8+1; h # numer kwantyla
## [1] 1013.8

Kolejnym krokiem będzie obliczenie wartości kwantyla na podstawie wzoru: \[\begin{equation} x_{\lfloor h \rfloor}+(h-{\lfloor h \rfloor})(x_{\lceil h\rceil}-x_{\lfloor h \rfloor}) \tag{9.4} \end{equation}\] gdzie: \(\lfloor h \rfloor\) to największa liczba całkowita nie większa od h oraz \(\lceil h \rceil\) to najmniejsza liczba całkowita nie mniejsza od h.

xL <- sz[floor(h)]; xP <- sz[ceiling(h)]
xL+(h-floor(h))*(xP-xL) # wartość kwantyla
## [1] 0.01779921

Teraz wykorzystamy gotową funkcję z pakietu stats:

quantile(z,0.80,type=7)
##        80% 
## 0.01779921

Otrzymane wartości kwantyli możemy również zaznaczyć na wykresie (rys. 9.3).

q <- as.numeric(quantile(z,c(0.25,0.5,0.75,0.80)))
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(ecdf(z))
arrows(q,c(0.25,0.5,0.75,0.80),q,c(0,0,0,0),length=0.1,angle=15,
       col=c("violetred3","YellowGreen","SteelBlue","wheat4"))
arrows(q,c(0.25,0.5,0.75,0.80),c(-5,-5,-5,-5),c(0.25,0.5,0.75,0.8),angle=0,
       col=c("violetred3","YellowGreen","SteelBlue","wheat4"))
points(q,c(0.25,0.5,0.75,0.8),bg="white",pch=21,
       col=c("violetred3","YellowGreen","SteelBlue","wheat4"))
legend("right", paste(c("Q25=", "Q50=", "Q75=", "Q80="),round(q,4)),bty="n",#lty=1,
       text.col=c("violetred3","YellowGreen","SteelBlue","wheat4"))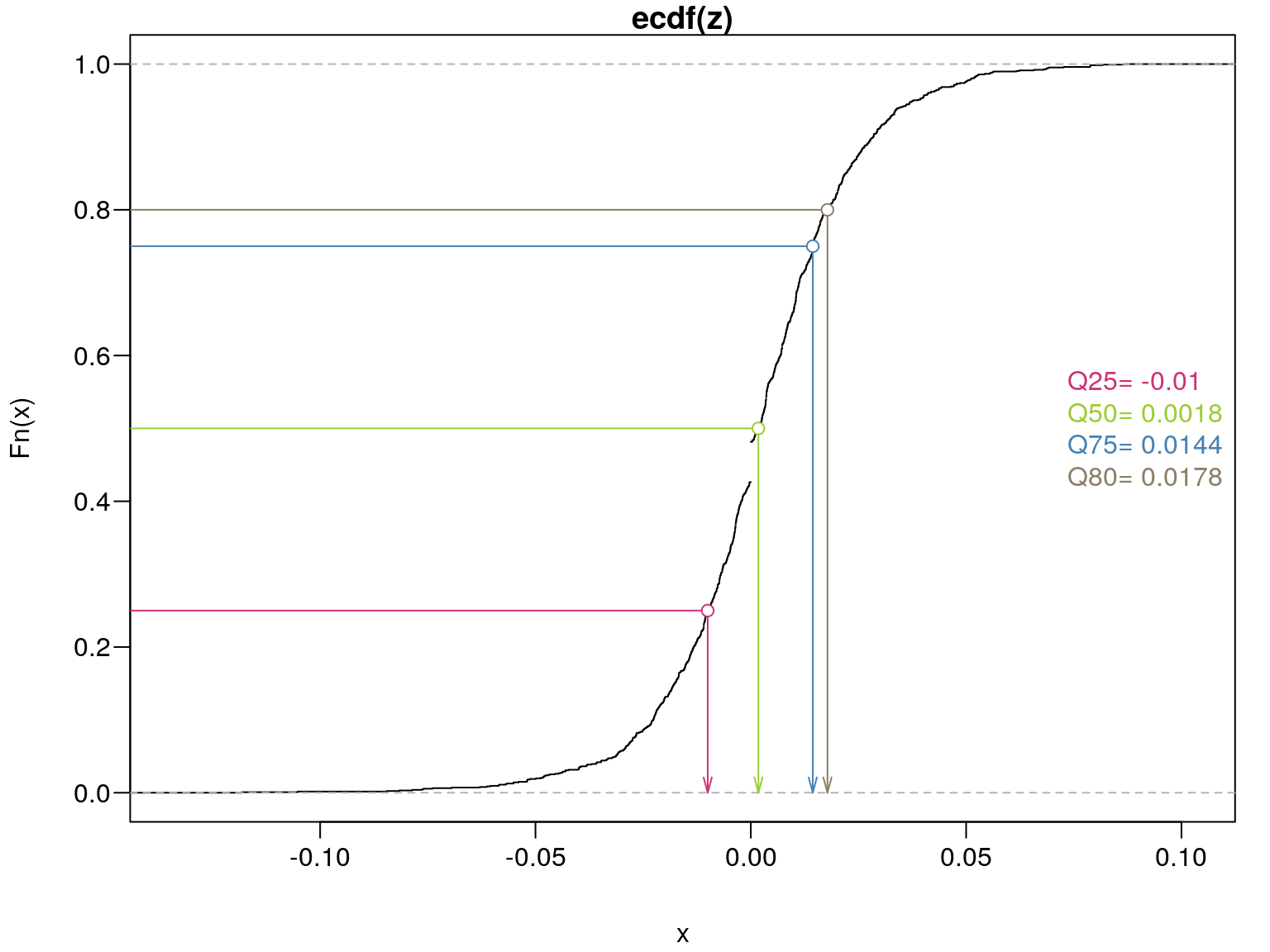
Dystrybuanta – prezentacja graficzna kwantyli.

Rysunek 9.3: Dystrybuanta – prezentacja graficzna kwantyli.

Wyznaczmy jeszcze wzory dla pozostałych metod szcowania kwantyli. Dla me- tod od 4 do 9 algorytmy różnią się tylko sposobem wyznaczenia numeru kwantyla. Wartość kwantyla jest obliczana tak jak to zostało przedstawione w powyższym przykładzie czyli według wzoru (9.4)

  • typ 4:

\[\begin{equation} h=n\cdot Q \tag{9.5} \end{equation}\]

  • typ 5:

\[\begin{equation} h=n\cdot Q + 1/2 \tag{9.6} \end{equation}\]

  • typ 6:

\[\begin{equation} h=(n+1)\cdot Q \tag{9.7} \end{equation}\]

  • typ 7:

\[\begin{equation} h=(n-1)\cdot Q + 1 \tag{9.8} \end{equation}\]

  • typ 8:

\[\begin{equation} h=(n+1/3)\cdot Q + 1/3 \tag{9.9} \end{equation}\]

  • typ 9:

\[\begin{equation} h=(n+1/4)\cdot Q + 3/8 \tag{9.10} \end{equation}\]

W przypadku metod od 1 do 3 do wyznaczenia numeru kwantyla oraz jego wartości korzystamy z nastęujących wzorów:

  • typ 1:

\[\begin{equation} h=n\cdot Q +1/2 \quad\wedge\quad x_{\lceil h-1/2\rceil} \tag{9.11} \end{equation}\]

  • typ 2:

\[\begin{equation} h=n\cdot Q +1/2 \quad\wedge\quad (x_{\lceil h-1/2\rceil}+x_{\lfloor h+1/2\rfloor})/2 \tag{9.12} \end{equation}\]

  • typ 3:

\[\begin{equation} h=n\cdot Q \quad\wedge\quad x_{[h]} \tag{9.13} \end{equation}\]

Za pomocą komendy quantile można także wyznaczyć jednocześnie kilka wartości dowolnych kwantyli:

quantile(z,c(0.17,0.60,0.83),type=7)
##          17%          60%          83% 
## -0.015450594  0.006886427  0.020418864

W różnych opracowaniach często spotykamy się z następującymi wzorami dotyczącymi skośności: \[\begin{equation} S_{1}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{\sqrt{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^3}} \tag{9.14} \end{equation}\]

(S1 <- e1071::skewness(z,type=1))
## [1] -0.2199644

\[\begin{equation} S_{2}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3\frac{\sqrt{n(n-1)}}{n-2}}{\sqrt{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)^3}} \tag{9.15} \end{equation}\]

(S2 <- e1071::skewness(z,type=2))
## [1] -0.2202252

\[\begin{equation} S_{3}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{s^3} \tag{9.16} \end{equation}\] gdzie \(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3\) oraz \(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\) to odpowiednio trzeci i drugi moment centralny oraz s to odchylenie standardowe z próby.

(S3 <- e1071::skewness(z,type=3))
## [1] -0.219704

Ponieważ obliczony wskaźnik skośności jest równy \(-0,22\) możemy sądzić, że rozkład stopy zwrotu charakteryzuje się niewielką lewostronną skośnością.

moments::agostino.test(z)
## 
##  D'Agostino skewness test
## 
## data:  z
## skew = -0.21996, z = -3.17810, p-value = 0.001483
## alternative hypothesis: data have a skewness

Również w przypadku miar koncentracji możemy spotkać się kilkoma wzorami na kurtozę: \[\begin{equation} K_{1}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{\left(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\right)}-3 \tag{9.17} \end{equation}\]

(K1 <- e1071::kurtosis(z,type=1))
## [1] 2.315957

\[\begin{equation} K_{2}=\frac{n(n+1)}{(n-1)(n-2)(n-3)}\sum_{i=1}^{n}\left(\frac{x_i-\bar{x}}{s}\right)^4-\frac{3(n-1)^2}{(n-2)(n-3)} \tag{9.18} \end{equation}\]

(K2 <- e1071::kurtosis(z,type=2))
## [1] 2.329873

\[\begin{equation} K_{3}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{s^4}-3 \tag{9.19} \end{equation}\] gdzie \(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4\) oraz \(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2\) to odpowiednio czwarty i drugi moment centralny oraz \(s\) to odchylenie standardowe z próby.

(K3 <- e1071::kurtosis(z,type=3))
## [1] 2.307569

Wysoka wartość kurtozy świadczy o tym, że rozkład stóp zwrotu charakteryzuje się spiczastością (rozkład leptokurtyczny) w stosunku do rozkładu normalnego (rozkład mezokurtyczny).

moments::anscombe.test(z)
## 
##  Anscombe-Glynn kurtosis test
## 
## data:  z
## kurt = 5.3160, z = 8.5299, p-value < 2.2e-16
## alternative hypothesis: kurtosis is not equal to 3

9.3 Rozkład normalny

Funkcja gęstości rozkładu normalnego \(N(\mu,\sigma)\) dla \(\mu\in R\) oraz \(\sigma>0\) czyli dnorm jest przedstawiona poniżej: \[\begin{equation} f(x)=\frac{1}{\sigma\sqrt(2\pi)}\exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right) \tag{9.20} \end{equation}\] gdzie: \(\mu\) to średnia, natomiast \(\sigma\) to odchylenie standardowe.

Do estymacji nieznanych parametrów rozkładu normalnego wykorzystamy następujące funkcję:

a <- mean(z); a # średnia
## [1] 0.00216913
b <- sd(z); b   # odchylenie standardowe
## [1] 0.02225315

W przypadku gdybyśmy chcieli estymować parametry \(\mu\) oraz \(\sigma\) za pomocą funkcji nlminb kod wyglądałby następująco:

# logarytm funkcji wiarygodności:
f1 <- function(theta, z) {
  sum(-dnorm(z, mean=theta[1], sd=theta[2], log=TRUE))
  }
# parametry startowe:
p.start <- c(mean(z), sd(z))
# optymalizacja funkcji f1:
e1 <- nlminb(p.start, f1, z=z, lower=c(-Inf,0), upper=c(Inf,Inf))
e1[c('par','objective')]
## $par
## [1] 0.002169126 0.022244371
## 
## $objective
## [1] -3023.984

Jak można zauważyć otrzymane parametry są dokładnie takie same jak te, które oszacowaliśmy za pomocą funkcji mean i sd.

W środowisku R można oszacować nieznane parametry również za pomocą funkcji MASS::fitdistr lub bardziej rozbudowanej wersji fitdistrplus::fitdist. Dla wbudowanych dystrybuant nie ma konieczności podawania parametrów startowych oraz ograniczeń przedziałowych. Takie opcje są bardzo użyteczne jeśli chcemy szukać parametrów dla dystrybuant zdefiniowanych przez nas.

summary(fitdistrplus::fitdist(z,'norm'))
## Fitting of the distribution ' norm ' by maximum likelihood 
## Parameters : 
##        estimate   Std. Error
## mean 0.00216913 0.0006249307
## sd   0.02224437 0.0004378806
## Loglikelihood:  3023.984   AIC:  -6043.968   BIC:  -6033.679 
## Correlation matrix:
##      mean sd
## mean    1  0
## sd      0  1

Znając już parametry \(\mu\) oraz \(\sigma\) możemy teraz przeprowadzić test zgodności Andersona-Darlinga i odpowiedzieć na pytanie: czy stopa zwrotu PKOBP pochodzi z rozkładu normalnego?

ADGofTest::ad.test(z,pnorm,mean(z),sd(z))
## 
##  Anderson-Darling GoF Test
## 
## data:  z  and  pnorm
## AD = 7.2474, p-value = 0.0002546
## alternative hypothesis: NA

Ponieważ \(p-value = 0.0002546\) to hipotetę zerową należy odrzucić. Zatem na poziomie istotności \(\alpha = 0,05\) należy stwierdzić, że stopa zwrotu PKOBP nie ma rozkładu normalnego. Naszą decyzję potwierdza także (rys. 9.4).

par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(density(z),col='SteelBlue',lwd=4,main='gęstość')
curve(dnorm(x,mean(z),sd(z)),add=TRUE,col='violetred3',lwd=3)
legend("topright",bg='white',bty="n",cex=1,lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))
plot(ecdf(z),col='SteelBlue',lwd=4,main='dystrybuanta')
curve(pnorm(x,mean(z),sd(z)),add=TRUE,col='violetred3',lwd=3)
legend("topleft",bg='white',bty="n",lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))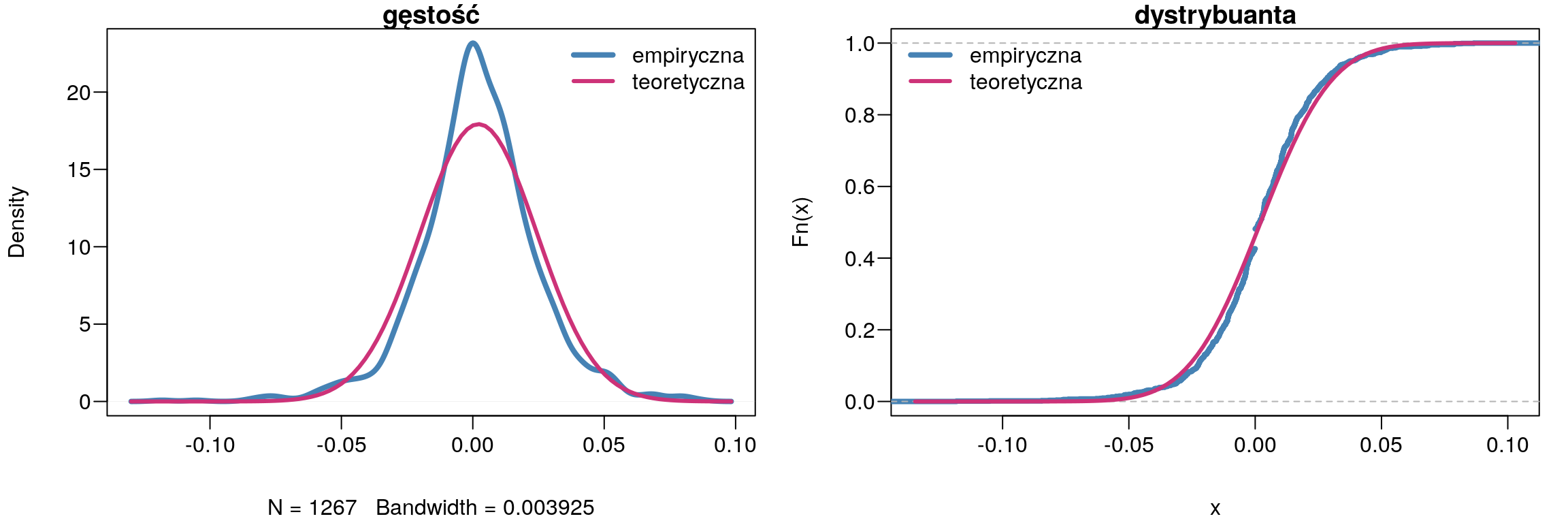
Porównanie wykresu gęstości z rozkładem normalnym.

Rysunek 9.4: Porównanie wykresu gęstości z rozkładem normalnym.

9.4 Rozkład Cauchy’ego

Funkcja gęstości rozkładu Cauchy’ego \(C(a, b)\) dla \(a \in R\) oraz \(b > 0\) czyli dcauchy jest przedstawiona poniżej: \[\begin{equation} f(x)=\frac{1}{\pi b \left(1+\left(\frac{x-a}{b}\right)^2\right)} \tag{9.21} \end{equation}\] gdzie: \(a\) to parametr położenia, natomiast \(b\) to parametr skali.

Tak samo jak w przypadku rozkładu normalnego, aby wykorzystać funkcję nlminb należy oszacować parametry startowe. Dla rozkładu Cauchy’ego można to zrobić w następujący sposób:

a <- median(z); a # parametr położenia: a
## [1] 0.001766785
b <- IQR(z)/2; b  # parametr skali: b
## [1] 0.0121972

Teraz metodą największej wiarygodności oszacujemy parametry rozkładu Cauche’go.

# logarytm funkcji wiarygodności:
f2 <- function(theta, z) {
  sum(-dcauchy(z, location=theta[1], scale=theta[2], log=TRUE))
  }
# parametry startowe:
p.start <- c(median(z), IQR(z)/2)
# optymalizacja funkcji f2:
e2 <- nlminb(p.start, f2, z=z, lower=c(-Inf,0), upper=c(Inf,Inf))
e2[c('par','objective')]
## $par
## [1] 0.002025263 0.011231456
## 
## $objective
## [1] -2945.315

Prawie identyczne wyniki otrzymamy przy wykorzystaniu funkcji fitdistrplus::fitdist.

summary(fitdistrplus::fitdist(z,'cauchy'))
## Fitting of the distribution ' cauchy ' by maximum likelihood 
## Parameters : 
##             estimate   Std. Error
## location 0.002029574 0.0004912212
## scale    0.011230842 0.0004071368
## Loglikelihood:  2945.315   AIC:  -5886.63   BIC:  -5876.341 
## Correlation matrix:
##            location      scale
## location 1.00000000 0.03089075
## scale    0.03089075 1.00000000

Do sprawdzenia zgoności rozkładu empirycznego z rozkładem Cauchy’ego zastosujemy test Andersona-Darlinga.

ADGofTest::ad.test(z,pcauchy, 0.002029574, 0.011230842)
## 
##  Anderson-Darling GoF Test
## 
## data:  z  and  pcauchy
## AD = 10.36, p-value = 3.782e-06
## alternative hypothesis: NA

Także i w tym razem na poziomie istotności \(\alpha = 0,05\) odrzucamy hipotezę zerową, która zakłada, że stopa zwrotu ma rozkład Cauchy’ego.

par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(density(z),col='SteelBlue',lwd=4,main='gęstość',ylim=c(0,30))
curve(dcauchy(x,0.002029574, 0.011230842),add=TRUE,col='violetred3',lwd=3)
legend("topright",bg='white',bty="n",cex=1,lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))
plot(ecdf(z),col='SteelBlue',lwd=4,main='dystrybuanta')
curve(pcauchy(x,0.002029574, 0.011230842),add=TRUE,col='violetred3',lwd=3)
legend("topleft",bg='white',bty="n",lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))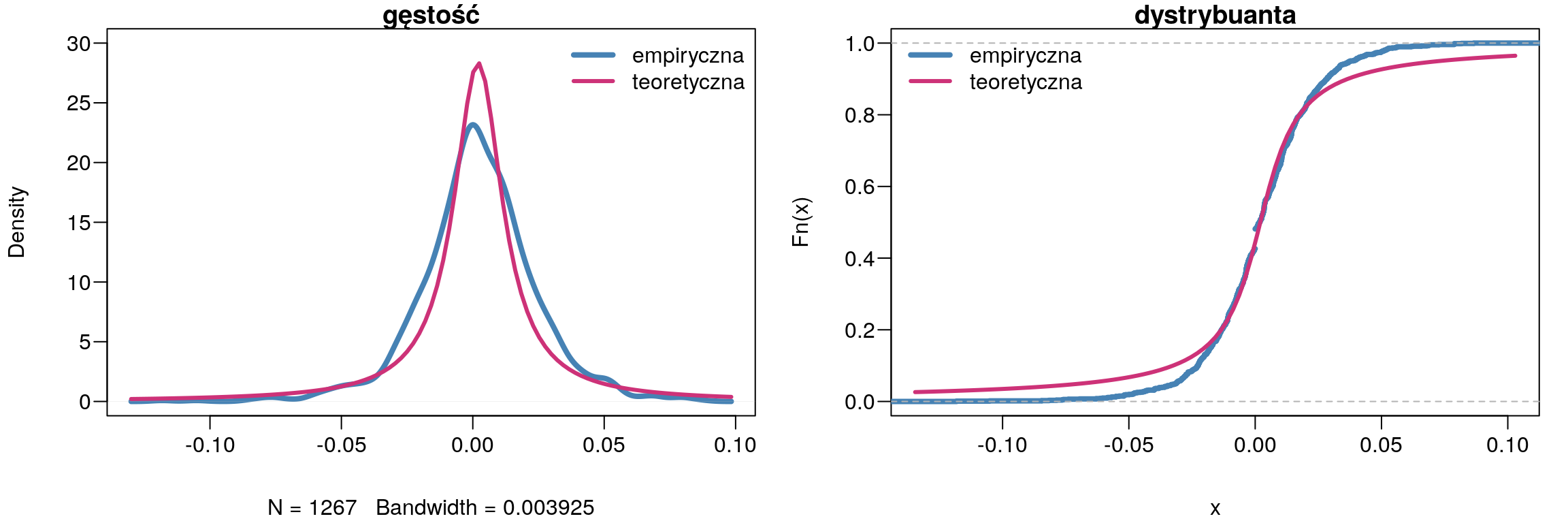
Porównanie wykresu gęstości z rozkładem Cauchy`ego.

Rysunek 9.5: Porównanie wykresu gęstości z rozkładem Cauchy`ego.

9.5 Rozkład Laplace’a

Funkcja gęstości rozkładu Laplace’a \(L(a, b)\) dla \(a \in R\) oraz \(b > 0\) czyli VGAM::dlaplace jest przedstawiona poniżej: \[\begin{equation} f(x)=\frac{1}{2b}\exp\left(\frac{-|x-a|}{b}\right) \tag{9.22} \end{equation}\] gdzie: \(a\) to parametr położenia, natomiast \(b\) to parametr skali.

Parametry startowe oszacujemy w następujący sposób:

a <- median(z); a     # parametr położenia: a
## [1] 0.001766785
b <- mean(abs(z-median(z))); b # parametr skali: b
## [1] 0.01628686

Mając do dyspozycji funkcję gęstości VGAM::dlaplace oraz parametry startowe dokonamy estymacji parametrów a oraz b dla rozkładu Laplace’a.

# logarytm funkcji wiarygodności:
f3 <- function(theta, z) {
  sum(-VGAM::dlaplace(z, location=theta[1], scale=theta[2], log=TRUE))
  }
# parametry startowe:
p.start <- c(median(z), mean(abs(z-median(z))))
# optymalizacja funkcji f3:
e3 <- nlminb(p.start, f3, z=z, lower=c(-Inf,0), upper=c(Inf,Inf))
e3
## $par
## [1] 0.001766785 0.016286861
## 
## $objective
## [1] -3071.524
## 
## $convergence
## [1] 1
## 
## $iterations
## [1] 1
## 
## $evaluations
## function gradient 
##       25        2 
## 
## $message
## [1] "false convergence (8)"

Stosowanie algorytmów optymalizacyjnych ogólnego przeznaczenia np. nlminb do wyznaczania parametrów funkcji wymaga podawania parametrów startowych. Jeśli nie chcemy ich podawać warto skorzystać z funkcj VGAM::vglm. Za jej pomocą można oszacować szukane parametry dla wielu ciekawych rozkładów np. Laplace’a.

fit <- VGAM::vglm(z ~ 1, VGAM::laplace, data.frame(z), trace=FALSE, crit="l")
VGAM::Coef(fit)
##    location       scale 
## 0.001766785 0.016296640
ADGofTest::ad.test(z,VGAM::plaplace, 0.001766785, 0.016296640)
## 
##  Anderson-Darling GoF Test
## 
## data:  z  and  VGAM::plaplace
## AD = 1.4474, p-value = 0.1896
## alternative hypothesis: NA

Ponieważ \(p-value = 0.1896\), więc nie ma podstaw do odrzucenia hipotezy zerowej. Zatem można przyjąć, że rozkład stóp zwrotu spółki PKOBP ma rozkład Laplace’a.

par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(density(z),col='SteelBlue',lwd=4,main='gęstość',ylim=c(0,30))
curve(VGAM::dlaplace(x,0.001766785, 0.016296640),add=TRUE,col='violetred3',lwd=3)
legend("topright",bg='white',bty="n",cex=1,lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))
plot(ecdf(z),col='SteelBlue',lwd=4,main='dystrybuanta')
curve(VGAM::plaplace(x,0.001766785, 0.016296640),add=TRUE,col='violetred3',lwd=3)
legend("topleft",bg='white',bty="n",lty=1,lwd=c(4,3),
       c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))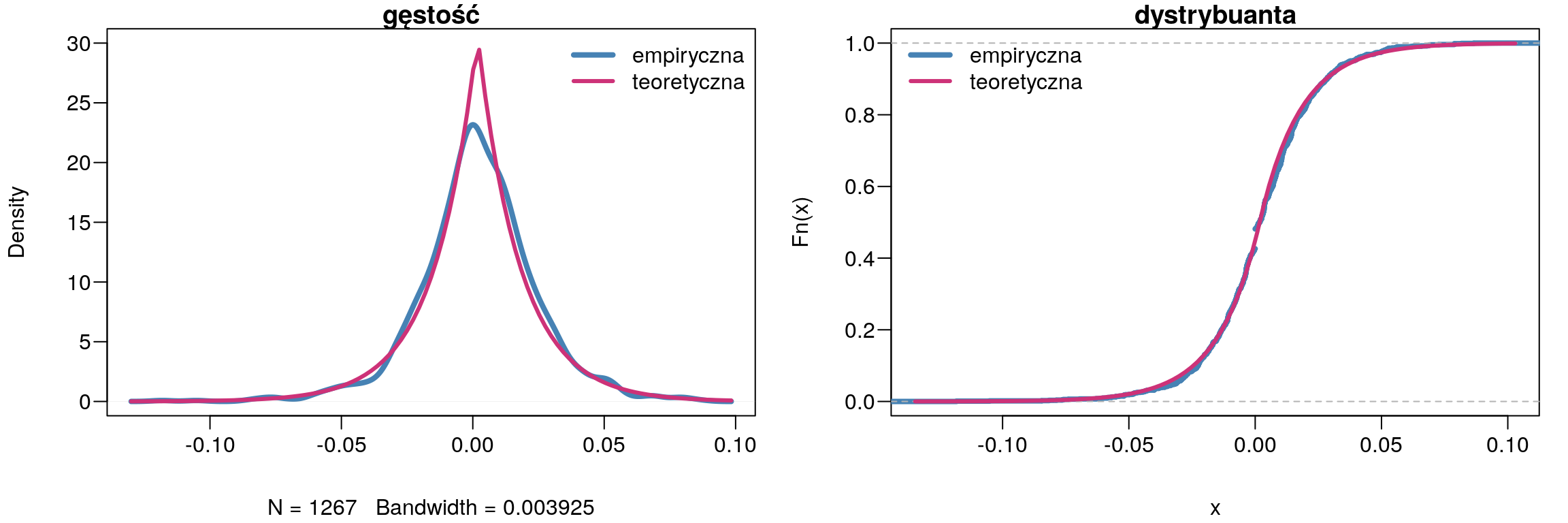
Porównanie wykresu gęstości z rozkładem Laplace`a.

Rysunek 9.6: Porównanie wykresu gęstości z rozkładem Laplace`a.

9.6 Rozkład Stabilny

Rozkład stabilny \(S(\alpha, \beta, \gamma, \delta)\), gdzie \(\alpha \in(0; 2)\) to parametr kształtu, \(\beta \in(-1; 1)\) to indeks skośności, \(\gamma > 0\) to parametr skali, oraz \(\delta \in R\) to parametr położenia, nie ma ściśle określonej funkcji gęstości – stabledist::dstable. W zależności od wartości parametrów \(\alpha\) oraz \(\beta\) możemy otrzymać rozkłady, takie jak: rozkład normalny: \(\alpha = 2\), rozkład Cauchy’ego: \(\alpha = 1\) i \(\beta = 0\) oraz rozkład Levy’ego: \(\alpha = 12\) i \(\beta = -1\).

Do oszacowania parametrów rozkładu stabilnego można wykorzystać funkcję libstableR::stable_fit_mle która stosuje metodę największej wiarygodności.

p <- libstableR::stable_fit_mle(z)
## INIT MCCULLCOH
p
## [1]  1.7281736156 -0.0007958884  0.0132426670  0.0023446287
ADGofTest::ad.test(z,stabledist::pstable,p[1],p[2],p[3],p[4])
## 
##  Anderson-Darling GoF Test
## 
## data:  z  and  stabledist::pstable
## AD = 0.72666, p-value = 0.5369
## alternative hypothesis: NA

Test Andersona-Darlinga wykazał, że badana zmienna ma rozkład stabilny o parametrach: \(\alpha = 1,73\), \(\beta = -0,000796\), \(\gamma = 0,01\) oraz \(\delta = 0,002\). Warto zwrócić uwagę na wysokość p-value dla rozkładu stabilnego, które wynosi \(0,5369\) i jest większa niż dla rozkładu Laplace’a \((0,1896)\). A zatem należy sądzić, że właśnie ten rozkład lepiej opisuje badaną zmienną (rys. 9.7).

par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(density(z),col='SteelBlue',lwd=4,main='gęstość')
curve(stabledist::dstable(x, 1.7281736156, -0.0007958884, 0.0132426670,  0.0023446287),
      add=TRUE,col='violetred3',lwd=3)
legend("topright",bg='white',bty="n",cex=1,lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))
plot(ecdf(z),col='SteelBlue',lwd=4,main='dystrybuanta')
curve(stabledist::pstable(x, 1.7281736156, -0.0007958884, 0.0132426670,  0.0023446287),
      add=TRUE,col='violetred3',lwd=3)
legend("topleft",bg='white',bty="n",lty=1,lwd=c(4,3),
c('empiryczna','teoretyczna'),col=c('SteelBlue','violetred3'))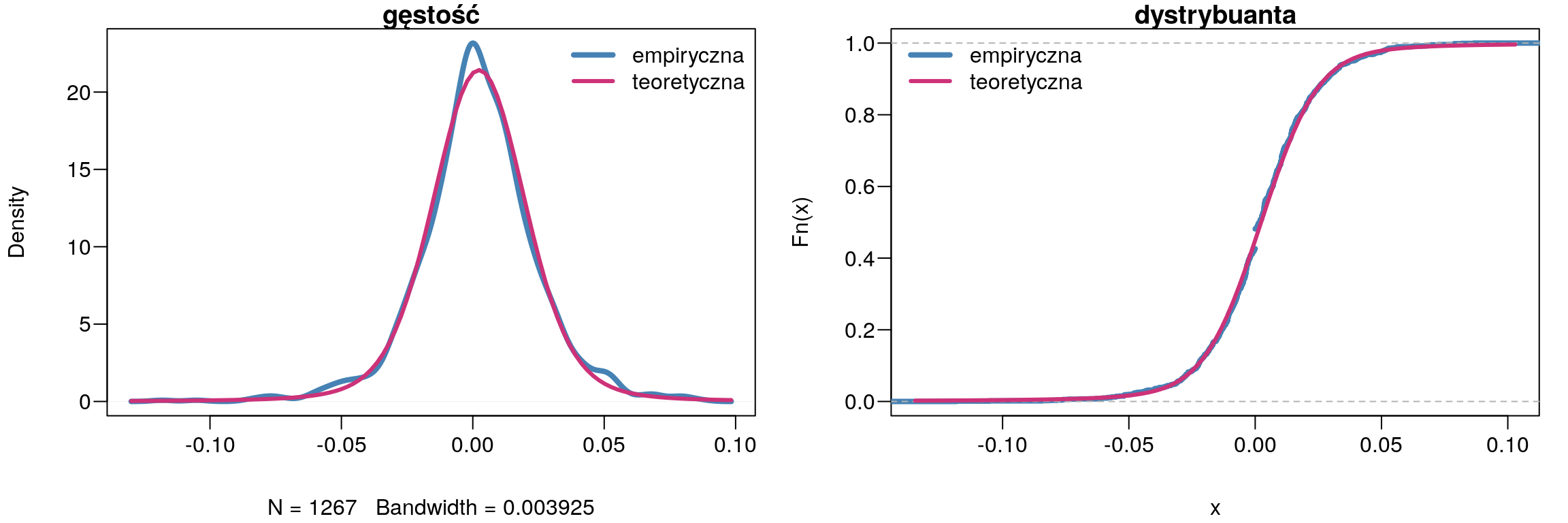
Porównanie wykresu gęstości z rozkładem Stabilnym.

Rysunek 9.7: Porównanie wykresu gęstości z rozkładem Stabilnym.

Znając rozkład badanej zmiennej można także obliczyć prawdopodobieństwo wystąpienia określonej stopy zwrotu. W tym celu wykorzystamy funkcję stabledist::pstable czyli dystrybuantę rozkładu stabilnego.

  1. Jakie jest prawdopodobieństwo, że stopa zwrotu będzie mniejsza niż \(2\%\)? \[P(z<0,02)\]
a <- p[1]
b <- p[2]
g <- p[3]
d <- p[4]
stabledist::pstable(0.02, a,b,g,d)
## [1] 0.821845
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      col='white', main='prawdopodobieństwo')
x <- seq(0.02,-0.1,length=300)
y <- stabledist::dstable(x,a,b,g,d)
polygon(c(0.02,x,-0.1),c(0,y,0),
        col='Violet',border = "Dark Magenta")
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      lwd=4,col='Dark Magenta',add=TRUE)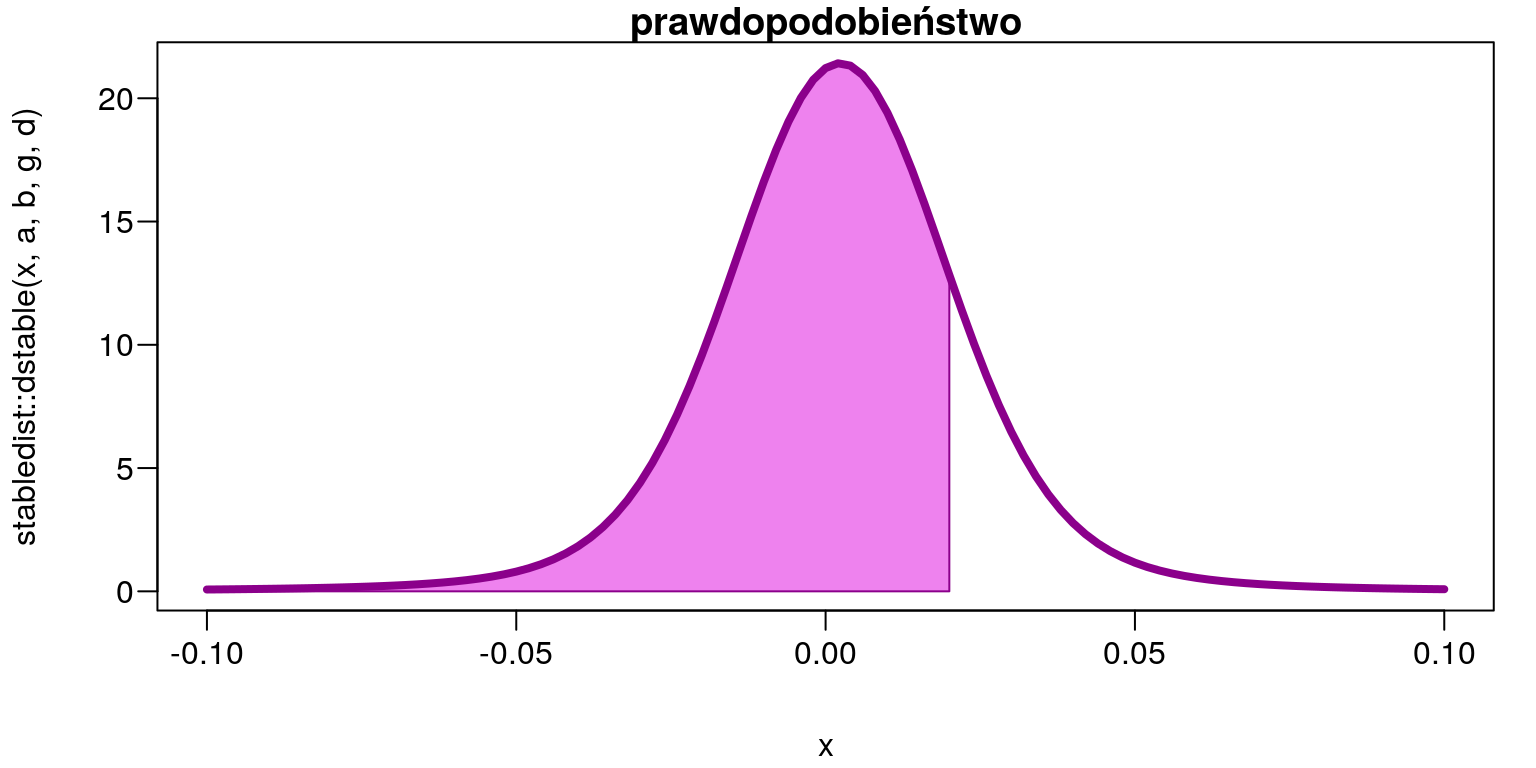
Obszar prawdopodobieństwa $P(z<0,02)=0,821845$

Rysunek 9.8: Obszar prawdopodobieństwa \(P(z<0,02)=0,821845\)

  1. Jakie jest prawdopodobieństwo, że stopa zwrotu będzie większa niż \(3,2\%\)? \[P(z > 0,032)\]
1-stabledist::pstable(0.032, a,b,g,d)
## [1] 0.07146513
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      col='white',main='prawdopodobieństwo')
x <- seq(0.032,0.1,length=300)
y <- stabledist::dstable(x,a,b,g,d)
polygon(c(0.032,x,0.1),c(0,y,0),
        col='Violet',border = "Dark Magenta")
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      lwd=4,col='Dark Magenta',add=TRUE)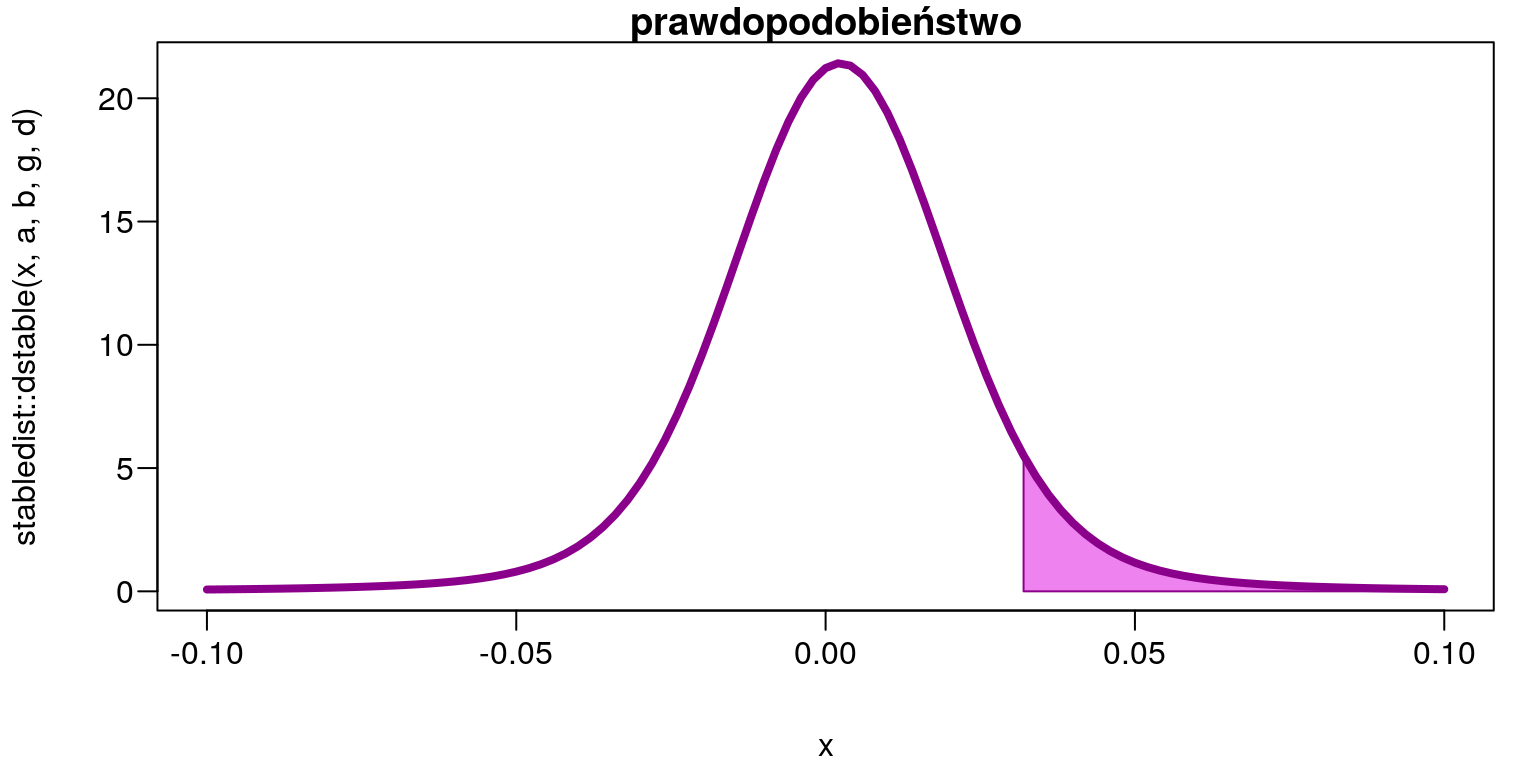
Obszar prawdopodobieństwa $P(z>0,032)=0,07146513$

Rysunek 9.9: Obszar prawdopodobieństwa \(P(z>0,032)=0,07146513\)

  1. Jakie jest prawdopodobieństwo, że stopa zwrotu będzie się zawierać w przedziale \((0\%; 3,78\%)\)? \[P(0<z<0,0378)\]
stabledist::pstable(0.0378, a,b,g,d)-stabledist::pstable(0, a,b,g,d)
## [1] 0.5038598
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      col='white',main='prawdopodobieństwo')
x <- seq(0,0.0378,length=300)
y <- stabledist::dstable(x,a,b,g,d)
polygon(c(0,x,0.0378),c(0,y,0),
        col='Violet',border = "Dark Magenta")
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      lwd=4,col='Dark Magenta',add=TRUE)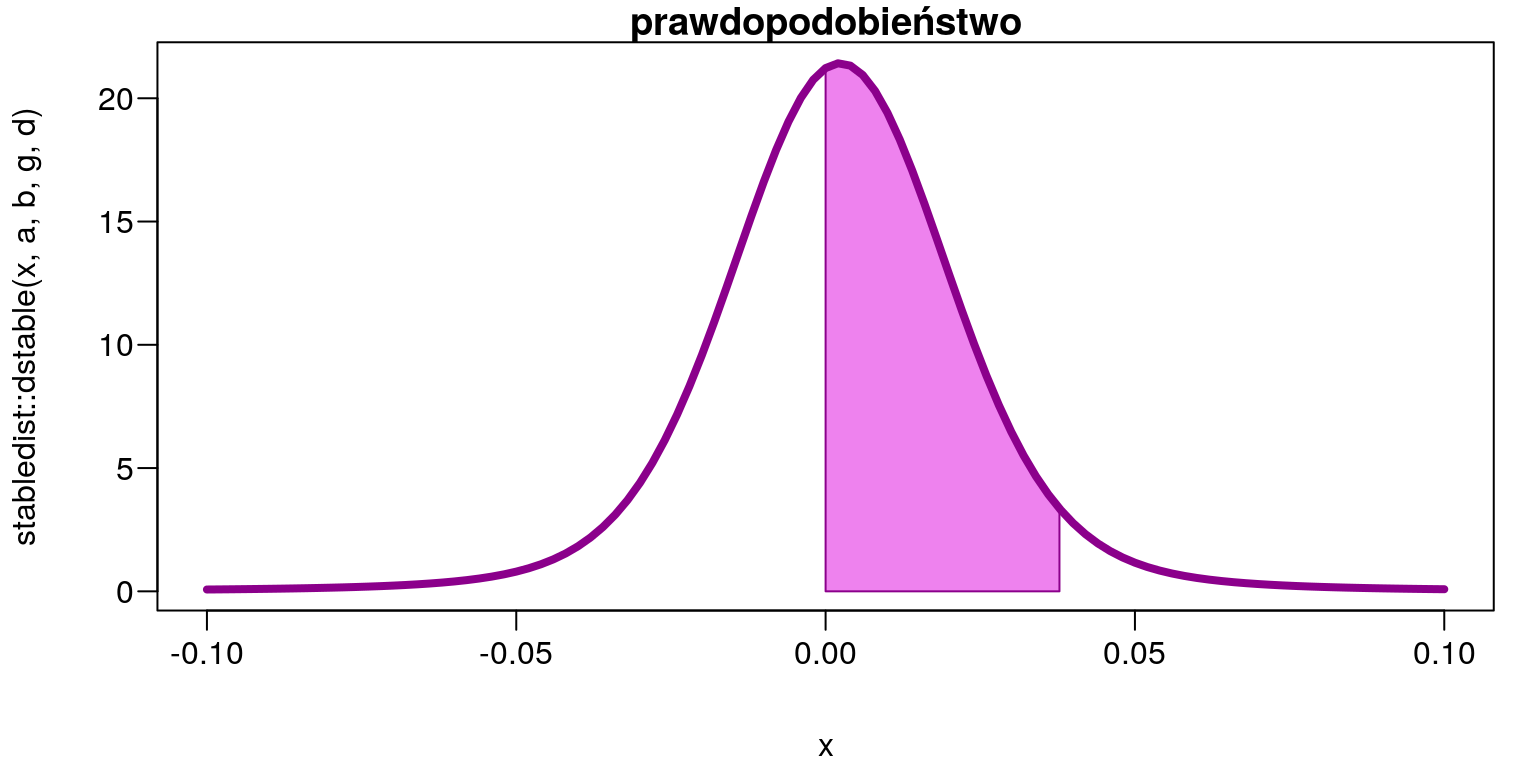
Obszar prawdopodobieństwa $P(0<z<0,0378)=0,5038598$

Rysunek 9.10: Obszar prawdopodobieństwa \(P(0<z<0,0378)=0,5038598\)

  1. Jakie jest prawdopodobieństwo, że stopa zwrotu będzie mniejsza niż \(1,75\%\) lub większa niż \(3,78\%\)? \[P (0,0175 > z > 0,0378)\]
stabledist::pstable(0.0175, a,b,g,d)+(1-stabledist::pstable(0.0378, a,b,g,d))
## [1] 0.8336819
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      col='white',main='prawdopodobieństwo')
x <- seq(-0.1,0.0175,length=300)
y <- stabledist::dstable(x,a,b,g,d)
polygon(c(-0.1,x,0.0175),c(0,y,0),
        col='Violet',border = "Dark Magenta")
x <- seq(0.0378,0.1,length=300)
y <- stabledist::dstable(x,a,b,g,d)
polygon(c(0.0378,x,0.1),c(0,y,0),
        col='Violet',border = "Dark Magenta")
curve(stabledist::dstable(x,a,b,g,d),-0.1,0.1,
      lwd=4,col='Dark Magenta',add=TRUE)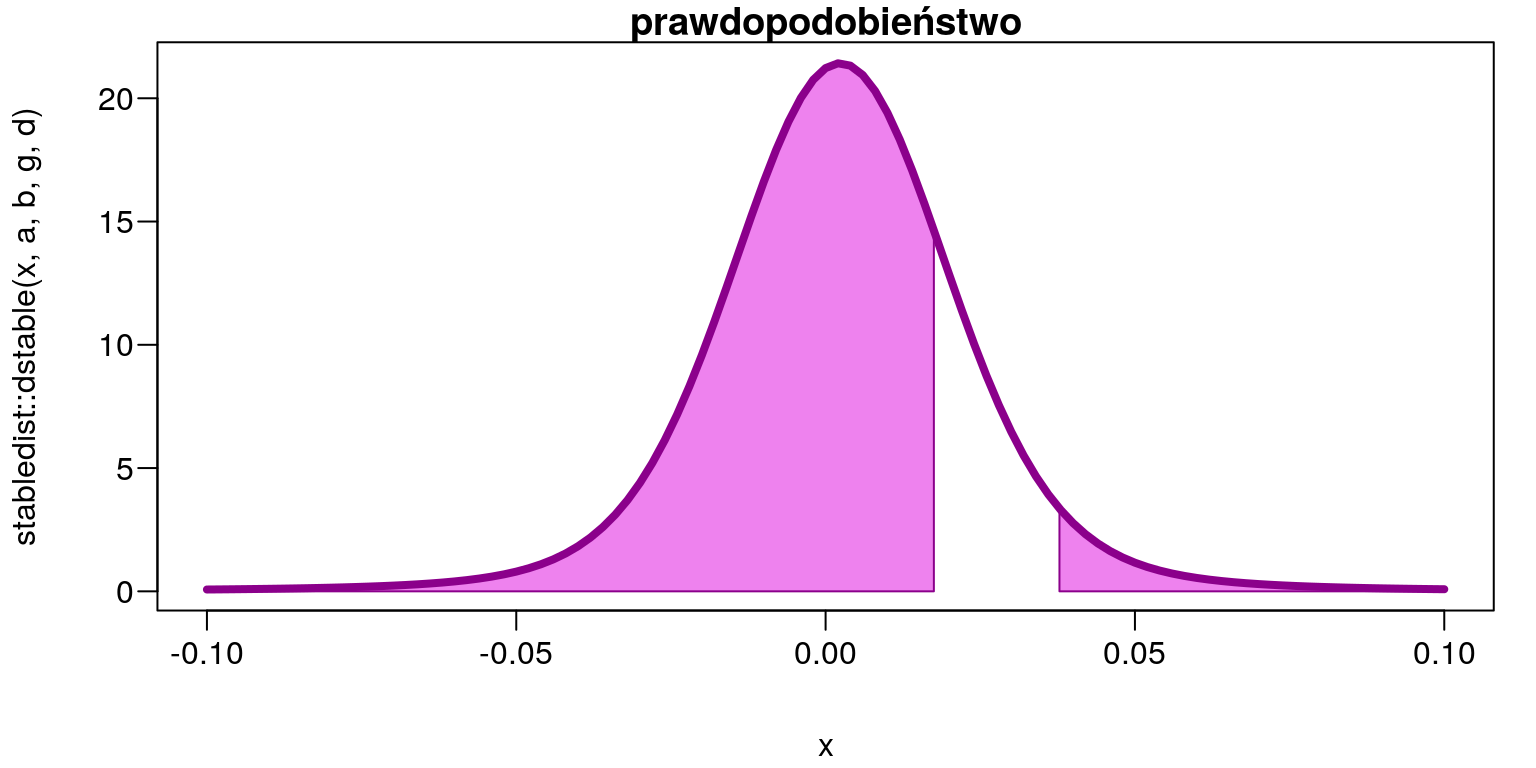
Obszar prawdopodobieństwa $P(0,0175>z>0,0378)=0,8336819$

Rysunek 9.11: Obszar prawdopodobieństwa \(P(0,0175>z>0,0378)=0,8336819\)

Na zakończenie warto jeszcze wspomnieć, że środowisko R oferuje także wiele innych rozkładów prawdopodobieństwa wraz z funkcjami do szacowania ich parametrów. W paczce fBasics oprócz funkcji do estymacji parametrów rozkładu stabilnego fBasic::stableFit mamy do dyspozycji takie rozkłady jak:

  • odwrotny rozkład normalny (Normal Inverse Gaussian Distribution) gdzie: dnig – funkcja gęstości, pnig – dystrybuanta, qnig – kwantyle, rnig – zmienne losowe, nigFit – estymacja parametrów.

  • rozkład hiperboliczny (Hyperbolic Distribution) gdzie: dhyp – funkcja gęstości, phyp – dystrybuanta, qhyp – kwantyle, rhyp – zmienne losowe, hypFit – estymacja parametrów.

  • uogolniony rozkład hiperboliczy (Generalized Hyperbolic Distribution) gdzie: dgh – funkcja gęstości, pgh – dystrybuanta, qgh – kwantyle, rgh – zmienne losowe, ghFit – estymacja parametrów.

  • uogolniony rozkład hiperboliczy t-Studenta (Generalized Hyperbolic Student-t) gdzie: dght – funkcja gęstości, pght – dystrybuanta, qght – kwantyle, rght – zmienne losowe, ghtFit – estymacja parametrów.

  • uogolniony rozkład lambda (Generalized Lambda Distribution) gdzie: dgld – funkcja gęstości, pgld – dystrybuanta, qgld – kwantyle, rgld – zmienne losowe, gldFit – estymacja parametrów.

Z kolei w bibliotece fGarch są zaimplementowane następujące rozkłady:

  • uogólniony rozkład błędów (Generalized Error Distribution – GED) gdzie: dged – symetryczna funkcja gęstości, gedFit – estymacja parametrów, dsged – skośna funkcja gęstości, sgedFit – estymacja parametrów.

  • rozkład t-Studenta (Student-t Distribution) gdzie: dstd – symetryczna funkcja gęstości, stdFit – estymacja parametrów, dsstd – skośna funkcja gęstości, sstdFit – estymacja parametrów.

  • rozkład normalny (Normal Distribution) gdzie: dnorm – symetryczna funkcja gęstości, normFit – estymacja parametrów, dsnorm – skośna funkcja gęstości, snormFit – estymacja parametrów.