Rozdział 2 Redukcja wymiaru

Metody redukcji wymiaru umożliwiają przedstawienie obserwacji w przestrzeni o zadanym wymiarze, niższym niż w przypadku oryginalnych danych.

Przedstawimy wybrane metody na przykładzie danych z różnych województw (zbiór danych daneGUS, patrz ostatni rozdział). Dla każdego z województw zebrano informację o liczbie studentów w tych województwach w rozbiciu na 16 grup kierunków. Każde województwo jest więc opisane wektorem 16 liczb.

Przypuśćmy, że chcemy przedstawić graficznie te województwa. Jak uwzględnić wszystkie 16 parametrów? Jednym z rozwiązań jest użycie metod redukcji wymiaru i liczby zmiennych z 16 do 2. Opisanie każdego z województw dwoma liczbami ułatwi przedstawianie graficzne tych województw.

Więc do dzieła!

Redukcja wymiaru często jest pośrednim etapem w zagadnieniu klasyfikacji, analizy skupień czy regresji. W określonych sytuacjach pozwala na poprawę skuteczności tych metod, zwiększa stabilność a czasem pozwala na uwzględnienie w analizach dużej liczby zmiennych. Jest też popularnie wykorzystywaną metodą do wizualizacji wielowymiarowych zmiennych, dane są redukowane do przestrzeni dwuwymiarowej, w której już łatwo je przedstawić na wykresie. Metody z tej grupy są również nazywane metodami ekstrakcji cech, ponieważ w wyniku redukcji wymiaru tworzone są nowe cechy, które mogą być wykorzystane do innych zagadnień.

2.1 Analiza składowych głównych (PCA, ang. Principal Components Analysis)

Analiza składowych głównych służy do wyznaczania nowych zmiennych, których możliwie mały podzbiór będzie mówił możliwie dużo o całej zmienności w zbiorze danych. Nowy zbiór zmiennych będzie tworzył bazę ortogonalną w przestrzeni cech. Zmienne będą wybierane w ten sposób by pierwsza zmienna odwzorowywała możliwie dużo zmienności w danych (po zrzutowaniu obserwacji na ten wektor, chcemy by wariancja rzutów była najwyższa). Po wyznaczeniu pierwszej zmiennej wyznaczamy drugą, tak by była ortogonalna do pierwszej, i wyjaśniała możliwie dużo pozostałej zmienności, kolejną zmienną wybieramy tak by była ortogonalna do dwóch pierwszych itd.

Tak uzyskany zbiór wektorów tworzy bazę ortogonalną w przestrzeni cech, a co więcej pierwsze współrzędne wyjaśniają większość zmienności w obserwacjach. Celem metody składowych głównych jest więc znalezienie transformacji układu współrzędnych, która lepiej opisze zmienność pomiędzy obserwacjami. Przykład takiej transformacji pokazujemy na rysunku 2.1. Przedstawiamy obserwacje w oryginalnym układzie współrzędnych (lewy rysunek) i w nowym układzie współrzędnych (prawy rysunek).

Rysunek 2.1: Przykład transformacji zmiennych z użyciem metody PCA.

W pakiecie R dostępnych jest kilka implementacji metody składowych głównych. Przedstawione poniżej najpopularniejsze wersje znajdują się w funkcjach prcomp(stats) i princomp(stats) z pakietu stats. Inne popularne wersje znaleźć można w funkcjach PCA(FactoMineR), cmdscale(stats) lub pca(pcurve).

Poszczególne implementacje różnią się metodami wykorzystanymi do znalezienia nowego układu zmiennych. W przypadku funkcji prcomp() nowe zmienne wyznaczane są z z użyciem dekompozycji na wartości osobliwe SVD. Ten sposób wyznaczania składowych głównych jest zalecany z uwagi na dużą dokładność numeryczną. W funkcji princomp() składowe główne są wyznaczane poprzez wektory własne macierzy kowariancji pomiędzy zmiennymi, używana jest więc dekompozycja spektralna. Teoretyczne właściwości wyznaczonych składowych głównych będą identyczne, jednak w określonych sytuacjach otrzymane wyniki dla poszczególnych funkcji mogą się różnić.

Poniższy kod pokazuje w jaki sposób działa funkcja princomp(). Wyznaczane są wektory własne macierzy kowariancji, tworzą one macierz przekształcenia dla danych.

kowariancja = cov(dane)
eig = eigen(kowariancja)
noweDane = dane %*% eig$vectors

Poniższy kod pokazuje w jaki sposób działa funkcja prcomp(). Wykorzystywana jest dekompozycja SVD.

svdr = svd(dane)
noweDane = dane %*% svdr$v

Obu funkcji do wyznaczania składowych głównych używa się w podobny sposób, kolejne argumenty określają zbiór danych (można wskazać macierz, ramkę danych, lub formułę określającą które zmienne mają być transformowane) oraz informacje czy zmienne powinny być uprzednio wycentrowane i przeskalowane. To czy dane przed wykonaniem analizy składowych głównych mają być przeskalowane zależy od rozwiązywanego problemu, w większości sytuacji skalowanie pozwala usunąć wpływ takich artefaktów jak różne jednostki dla poszczególnych zmiennych. W obiektach przekazywanych jako wynik przez obie funkcje przechowywane są podobne informa- cje, choć w polach o różnej nazwie. Wynikiem funkcji prcomp() jest obiekt klasy prcomp, którego pola są wymienione w tabeli 2.1.

Tabela 2.1: Pola obiektu klasy $\texttt{prcomp}$.
.	opis
$\texttt{\$sdev}$	Wektor odchyleń standardowych dla obserwacji. Kolejne zmienne odpowiadają odchyleniom standardowym liczonym dla kolejnych składowych głównych.
$\texttt{\$rotation}$	Macierz obrotu przekształcająca oryginalny układ współrzędnych w nowy układ współrzędnych.
$\texttt{\$center}$	Wektor wartości wykorzystanych przy centrowaniu obserwacji.
$\texttt{\$scale}$	Wektor wartości wykorzystanych przy skalowaniu obserwacji.
$\texttt{\$x}$	Macierz współrzędznych kolejnych obserwacji w nowym układzie współrzędnych, macierz ta ma identyczne wymiary co oryginalny zbiór zmiennych.

Dla obiektów klasy prcomp dostępne są przeciążone wersje funkcji plot(), summary(), biplot(). Poniżej przedstawiamy przykładowe wywołanie tych funkcji. Graficzny wynik ich działania jest przedstawiony na rysunku 2.2. Lewy rysunek przedstawia wynik dla funkcji plot() a prawy przedstawia wynik funkcji biplot() wykonanych dla argumentu klasy prcomp. Na lewym rysunku przedstawione są wariancje wyjaśnione przez kolejne wektory nowego układu współrzędnych. Ta informacja jest podawana również przez funkcje summary(). Prawy rysunek przedstawia biplot, na którym umieszczone są dwa wykresy. Jeden przedstawia indeksy obserwacji przedstawione na układzie współrzędnych określonych przez dwie pierwsze składowe główne (w tym przypadku dwie współrzędne wyjaśniają około $50\%$ całej zmienności). Drugi rysunek przedstawia kierunki w których działają oryginalne zmienne, innymi słowy przedstawiają jak wartość danej zmiennej wpływa na wartości dwóch pierwszych składowych głównych.

Jeżeli wektory mają przeciwne zwroty to dane zmienne są ujemnie skorelowane (nie można jednak ocenić wartości korelacji), jeżeli zwroty są prostopadłe to zmienne są nieskorelowane, a jeżeli zwroty są bliskie to zmienne są dodatnio skorelowane.

daneO <- read.table("http://www.biecek.pl/R/dane/daneO.csv",sep=";",header = TRUE)
# przygotowujemy dane, usuwamy zmienne jakościowe i brakujące przypadki
dane = na.omit(daneO[,-c(4,5,6,7)])
# wykonujemy analizę składowych głównych, normalizując wcześniej zmienne
wynik = prcomp(dane, scale=T)
# jak wygląda obiekt z wynikami od środka
str(wynik)

## List of 5
##  $ sdev    : num [1:5] 1.153 1.068 0.963 0.916 0.873
##  $ rotation: num [1:5, 1:5] 0.5016 0.0935 -0.4244 0.4878 -0.5671 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:5] "Wiek" "Rozmiar.guza" "Wezly.chlonne" "Okres.bez.wznowy" ...
##   .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
##  $ center  : Named num [1:5] 45.417 1.271 0.417 37.406 2640.896
##   ..- attr(*, "names")= chr [1:5] "Wiek" "Rozmiar.guza" "Wezly.chlonne" "Okres.bez.wznowy" ...
##  $ scale   : Named num [1:5] 6.206 0.447 0.496 9.527 3616.045
##   ..- attr(*, "names")= chr [1:5] "Wiek" "Rozmiar.guza" "Wezly.chlonne" "Okres.bez.wznowy" ...
##  $ x       : num [1:96, 1:5] -1.5446 0.0105 -1.4565 -1.2352 -1.2541 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:96] "1" "2" "3" "4" ...
##   .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
##  - attr(*, "class")= chr "prcomp"

# zamiast obrazka możemy tę informację mieć przedstawioną jako ramkę danych
summary(wynik)

## Importance of components:
##                           PC1    PC2    PC3    PC4    PC5
## Standard deviation     1.1534 1.0684 0.9629 0.9157 0.8733
## Proportion of Variance 0.2661 0.2283 0.1854 0.1677 0.1525
## Cumulative Proportion  0.2661 0.4943 0.6798 0.8475 1.0000

par(mfcol=c(1,2))
# ten wykres przedstawia ile wariancji jest wyjaśnione przez kolejne zmienne
plot(wynik)
# narysujmy biplot dla tych wyników
biplot(wynik)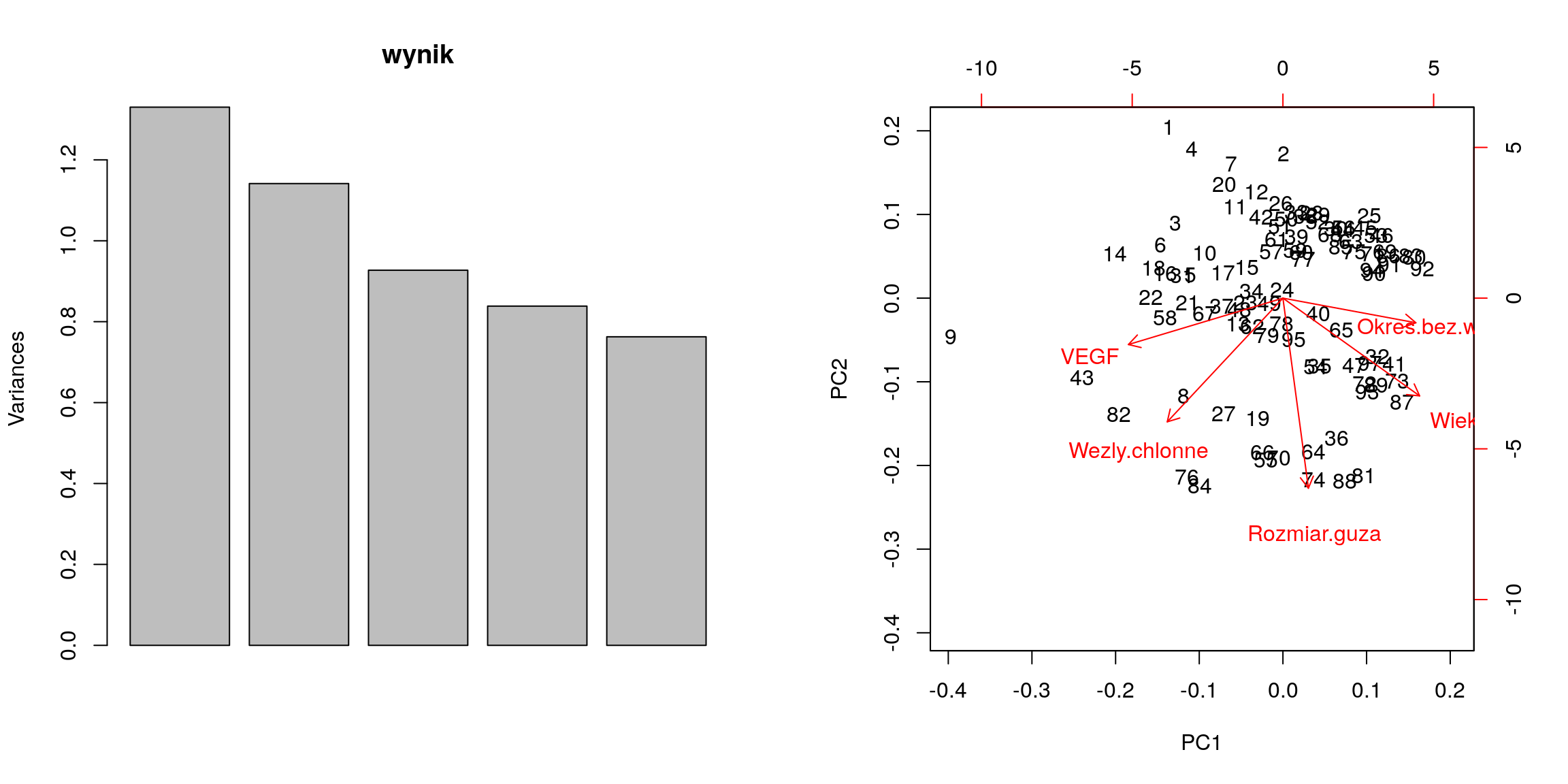

Rysunek 2.2: Graficzna reprezenacja wyników funkcji prcomp().

I jeszcze przykład dla danych GUSowskich

daneGUS <- read.table("http://www.biecek.pl/R/dane/Dane2007GUS.csv", sep=";", h=T, dec=",")
# przygotowujemy dane, wybieramy tylko kolumny dotyczące studentów
dane = daneGUS[,5:19]
# wykonujemy analizę składowych głównych
wynik = prcomp(dane, scale=T)
# zamiast obrazka możemy tę informację mieć przedstawioną jako ramkę danych
summary(wynik)

## Importance of components:
##                           PC1     PC2     PC3     PC4    PC5     PC6
## Standard deviation     3.3274 1.19941 0.84435 0.74182 0.5666 0.50895
## Proportion of Variance 0.7381 0.09591 0.04753 0.03669 0.0214 0.01727
## Cumulative Proportion  0.7381 0.83400 0.88153 0.91821 0.9396 0.95688
##                            PC7     PC8     PC9    PC10    PC11    PC12
## Standard deviation     0.45921 0.42930 0.36576 0.25868 0.16275 0.11174
## Proportion of Variance 0.01406 0.01229 0.00892 0.00446 0.00177 0.00083
## Cumulative Proportion  0.97094 0.98323 0.99215 0.99661 0.99837 0.99920
##                           PC13    PC14     PC15
## Standard deviation     0.09009 0.06113 0.008919
## Proportion of Variance 0.00054 0.00025 0.000010
## Cumulative Proportion  0.99975 0.99999 1.000000

par(mfcol=c(1,2))
# ten wykres przedstawia ile wariancji jest wyjaśnione przez kolejne zmienne
plot(wynik)
# narysujmy biplot dla tych wyników
biplot(wynik)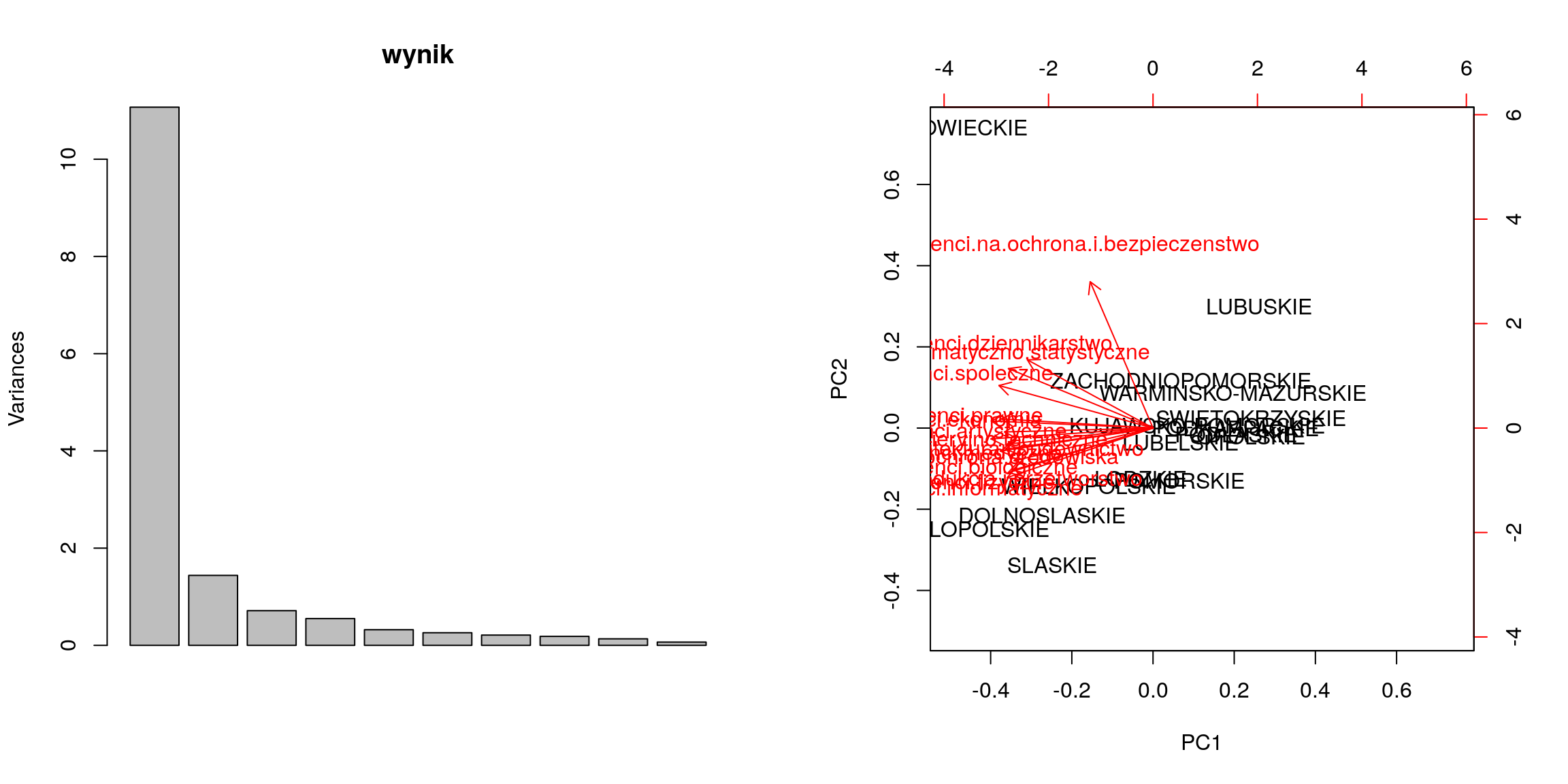

Rysunek 2.3: Graficzna reprezenacja wyników PCA dla danych GUSowych.

Zobaczmy jak wygląda macierz przekształcenia. Można z niej odczytać w jaki sposób poszczególne współrzędne wpływają na kolejne składowe.

W przypadku pierwszej składowej współczynniki przy praktycznie każdej zmiennej wynoszą około $-0,25$. W przybliżeniu oznacza to, że pierwsza składowa będzie odpowiadała -łącznej liczbie studentów w danym województwie. A więc im więcej studentów tym mniejsza wartość pierwszej składowej.

Druga składowa jest już ciekawsza, ponieważ różnym województwom odpowiadają różne współczynniki. Województwa o dużych wartościach na drugiej składowej to województwa z “nadreprezentacją” studentów z kierunków społecznych, dziennikarstwa, matematyki i ochrony a “niedomiarze” studentów z nauk biologicznych, fizycznych, informatycznych i produkcji.

# macierz przekształcenia
wynik$rotation[,1:4]

##                                             PC1         PC2         PC3
## studenci.artystyczne                 -0.2668431 -0.01935350 -0.39012931
## studenci.spoleczne                   -0.2769475  0.21209089 -0.06445972
## studenci.ekonomia                    -0.2908474  0.03508728 -0.12031553
## studenci.prawne                      -0.2724967  0.04551798 -0.11257234
## studenci.dziennikarstwo              -0.2258601  0.34018454  0.43605864
## studenci.biologiczne                 -0.2496580 -0.16285221  0.32214165
## studenci.fizyczne                    -0.2604590 -0.22242474 -0.24023057
## studenci.matematyczno.statystyczne   -0.2599768  0.29657185  0.03841079
## studenci.informatyczne               -0.2621867 -0.24703158 -0.01225057
## studenci.medyczne                    -0.2654754 -0.10490797 -0.44763987
## studenci.inzynieryjno.techniczne     -0.2913698 -0.05414636  0.02117248
## studenci.produkcja.i.przetworstwo    -0.2521053 -0.20996741  0.24515891
## studenci.architektura.i.budownictwo  -0.2621286 -0.08025265  0.42188743
## studenci.na.ochrona.srodowiska       -0.2744594 -0.11530401  0.07394037
## studenci.na.ochrona.i.bezpieczenstwo -0.1129936  0.72998765 -0.13728919
##                                              PC4
## studenci.artystyczne                  0.06339131
## studenci.spoleczne                   -0.18107667
## studenci.ekonomia                     0.01692755
## studenci.prawne                       0.27527826
## studenci.dziennikarstwo               0.37212854
## studenci.biologiczne                  0.40296643
## studenci.fizyczne                     0.28846603
## studenci.matematyczno.statystyczne    0.13851583
## studenci.informatyczne               -0.33688023
## studenci.medyczne                     0.09636022
## studenci.inzynieryjno.techniczne     -0.08996322
## studenci.produkcja.i.przetworstwo    -0.39126146
## studenci.architektura.i.budownictwo  -0.15234913
## studenci.na.ochrona.srodowiska       -0.29601767
## studenci.na.ochrona.i.bezpieczenstwo -0.29845944

2.2 Nieliniowe skalowanie wielowymiarowe (Sammon Mapping)

W przypadku metody PCA nowe współrzędne konstruowano tak, by były one kombinacjami liniowymi oryginalnych danych. To oczywiście nie jest jedyna możliwość konstrukcji nowych zmiennych. Postawmy zagadnienie skalowania następująco.

Dane: mamy $n$ obiektów oraz macierz odległości pomiędzy każdą parą obiektów. Oznaczmy przez $d_ij$ odległość pomiędzy obiektem $i$-tym i $j$-tym. Szukane: reprezentacja obiektów w przestrzeni $k$ wymiarowej, tak by zminimalizować \[ stress=\frac{\sum_{ij}(d_{ij}-\bar{d}_{ij})^2/d_{ij}}{\sum_{ij}d_{ij}} \] gdzie $\tilde{d}_{ij}$ to odległość pomiędzy obiektami $i$ i $j$ w nowej $k$-wymiarowej przestrzeni.

Innymi słowy, szukamy (niekoniecznie liniowego) przekształcenia, które możliwie najwierniej (w sensie ważonego błędu kwadratowego) zachowa odległości pomiędzy obiektami. Takie przekształcenie poszukiwane jest iteracyjnie.

Jak to zrobić w R? Można np. używając funkcji sammon(MASS). Pierwszym argumentem tej funkcji powinna być macierz odległości pomiędzy obiektami (np. wynik funkcji dist()) a argument k określa na iluwymiarową przestrzeń chcemy skalować dane (domyślnie $k = 2$).

# wyznaczamy macierz odległości
odleglosci = dist(dane)
# wyznaczamy nowe współrzędne w przestrzeni dwuwymiarowej
noweSammon = MASS::sammon(odleglosci, k=2, trace=FALSE)
# jak wyglądają nowe współrzędne
head(noweSammon$points)

##                          [,1]      [,2]
## DOLNOSLASKIE        15211.180 3403.2348
## KUJAWSKO-POMORSKIE  -7063.770 3448.9048
## LODZKIE              1251.418 -916.5612
## LUBELSKIE           -4912.805 1058.6175
## LUBUSKIE           -12775.224 3090.0001
## MALOPOLSKIE         21526.869 1963.5498

Tabela 2.2: Pola obiektu będącego wynikiem funkcji sammon().
.	opis
$\texttt{\$points}$	Macierz współrzędnych obiektów w nowej $k$-wymiarowej przestrzeni.
$\texttt{\$stress}$	Uzyskana wartość optymalizowanego parametru stresu.

2.3 Skalowanie wielowymiarowe Kruskalla (MDS, ang. Multidimensional Scaling)

Jak już wspominaliśmy, metody redukcji wymiaru są często wykorzystywane do wizualizacji danych. W przypadku analizy składowych głównych po znalezieniu współrzędnych obiektów w nowej bazie wystarczy wziąć dwie pierwsze współrzędne by móc przedstawiać zbiór obserwacji na wykresie dwuwymiarowym, trzy pierwsze by móc przedstawić zbiór obserwacji na wykresie trójwymiarowym itp. Wadą analizy składowych głównych jest uwzględnianie wyłącznie zmiennych ilościowych. Kolejnym minusem jest konieczność posiadania wartości pomiarów dla kolejnych zmiennych, nie można tej metody użyć w sytuacji gdy mamy wyłącznie informacje o podobieństwie lub odległości pomiędzy obiektami.

Metody skalowania Sammona i Kruskala nie mają tych wad. Są to metody ekstrakcji cech, na podstawie macierzy odległości lub macierzy niepodobieństwa pomiędzy obiektami. Celem tych metod jest wyznaczenie współrzędnych w nowym układzie współrzędnych, w taki sposób by odległości pomiędzy obiektami w nowym układzie współrzędnych były podobne do oryginalnych odległości pomiędzy obiektami. Przykład skalowania wielowymiarowego przedstawiliśmy na rysunku 2.4.

W przypadku skalowania Kruskala minimalizowana jest wartość \[ stress=\frac{\sum_{ij}(f(d_{ij})-\tilde{d}_{ij})^2}{\sum_{ij}f(d_{ij})^2}, \] gdzie $\tilde{d}_{ij}$ to odległość pomiędzy obiektami $i$ i $j$ w nowej $k$-wymiarowej przestrzeni a d ij to oryginalne odległości pomiędzy obiektami przekształcone przez pewną monotoniczną funkcję $f()$ (więc $d_{ij}$ i $\tilde{d}_{ij}$ mogą być w różnych skalach!).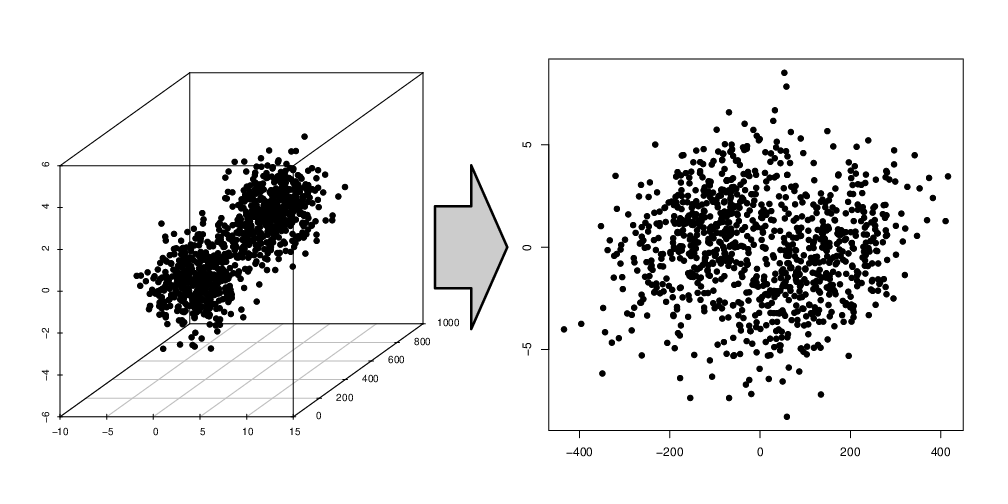

Rysunek 2.4: Przykład skalowania wielowymiarowego.

Skalowanie wielowymiarowe jest w R dostępne w kilku funkcjach:

funkcja isoMDS(MASS) wyznacza niemetryczne skalowanie Kruskala,
funkcja sammon(MASS) wyznacza niemetryczne skalowanie Sammona (patrz poprzedni podrozdział [TODO: uspójnić!!]),
funkcja cmdscale(stats) wyznacza skalowanie metryczne inaczej PCA (patrz poprzedni podrozdział [TODO: uspójnić!!]).

Poniżej przedstawimy przykłady użycia dla funkcji isoMDS(), z pozostałych korzysta się podobnie. Najważniejszym argumentem wejściowym do algorytmu skalowania wielowymiarowego jest macierz odległości pomiędzy obserwacjami. Wyznaczyć ją można np. funkcją dist(stats). W funkcji dist() zaimplementowane są wszystkie popularne metody liczenia odległości pomiędzy obserwacjami, w tym odległość euklidesowa (najpopularniejsza, odpowiadająca sumie kwadratów różnic poszczególnych współrzędnych, tej odległości odpowiada argument method="euclidean"), odległość Manhattan, nazywana też odległością taksówkową lub miejską (suma modułów różnic pomiędzy współrzędnymi, argument method="manhattan"), odległość Mińkowskiego (argument method="minkowski") oraz kilka innych mniej popularnych odległości. Jeżeli w zbiorze danych znajdują się zmienne jakościowe to funkcja dist() sobie z nimi nie poradzi. W takiej sytuacji lepiej wykorzystać funkcję daisy(cluster) wyznaczającą macierz niepodobieństwa pomiędzy obiektami. Funkcja daisy() uwzględnia również zmienne jakościowe (poniżej przedstawiamy przykład użycia). Macierz odległości jest obiektem klasy dist() i nie jest pamiętana jako macierz, a jedynie jako połowa macierzy (ponieważ odległość jest symetryczna szkoda pamięci na przechowywanie nadmiarowych danych). Jeżeli potrzebujemy przekształcić obiekt dist() na macierz to możemy wykorzystać funkcję as.matrix()

Wynikiem algorytmu skalowania wielowymiarowego są współrzędne obserwacji w pewnym nowym układzie współrzędnych. Możemy wybrać wymiar przestrzeni na jaką mają być przeskalowane dane (argument k funkcji isoMDS). Z pewnością po wykonaniu skalowania interesować nas będzie na ile skalowanie zachowało odległości pomiędzy obiektami, czy dużo jest znacznych zniekształceń. Do oceny wyników skalowania wykorzystać można wykres Sheparda przedstawiający na jednej osi oryginalne odległości pomiędzy obiektami a na drugiej osi odległości w nowym układzie współ rzędnych. Do wyznaczenia obu wektorów odległości służy funkcja Shepard(MASS), można też skorzystać z wrappera na tę funkcję, czyli z funkcji stressplot(vegan).

Poniżej przedstawiamy przykład skalowania wielowymiarowego. Wykorzystamy tę metodę do przedstawienia za pomocą dwuwymiarowego wykresu podobieństw pomiędzy pacjentkami ze zbioru danych daneO. Graficzny wynik tych analiz jest przedstawiony na rysunku 2.5. Lewy rysunek przedstawia pacjentki w nowym dwuwymiarowym układzie współrzędnych, w tym przypadku pacjentki przedstawiane są jako punkty. Wypełniony punkt oznacza dla niepowodzenie leczenia a więc wznowę, a pusty w środku w oznacza wyleczenie pozytywne (widzimy, że pacjentki z niepo- wodzeniami grupują się blisko siebie). Ciekawym było by naniesienie na ten wykres nazwisk pacjentek i porównanie, które pacjentki pod względem zmierzonych wartości były do siebie podobne. Prawy rysunek przedstawia dokładność skalowania, a więc jak oryginalne odległości mają się do odległości w nowym układzie współrzędnych.

dane0 <- read.table("http://www.biecek.pl/R/dane/dane0.csv",sep=";",header = TRUE)
# konstruujemy macierz niepodobieństwa pomiędzy pacjentkami, również zmienne jakościowe są uwzględnione
niepodobienstwa = cluster::daisy(daneO)

## Warning in cluster::daisy(daneO): binary variable(s) 2, 3 treated as
## interval scaled

# przeprowadzamy skalowanie niemetryczne, skalujemy do przestrzeni o
# dwóch wymiarach
skalowanie = MASS::isoMDS(niepodobienstwa, k=2)

## initial  value 30.138174 
## iter   5 value 25.846808
## final  value 25.531983 
## converged

# obiekt wynikowy zawiera współrzędne obserwacji w~nowym układzie współrzędnych
str(skalowanie)

## List of 2
##  $ points: num [1:97, 1:2] 0.1011 0.3147 -0.1055 0.2811 -0.0604 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:97] "1" "2" "3" "4" ...
##   .. ..$ : NULL
##  $ stress: num 25.5

# konstruujemy wektor pomocniczy do rysowania
ksztalty = ifelse(daneO$Niepowodzenia=="brak", 21, 19)

par(mfcol=c(1,2))
# rysujemy pacjentki w~nowym układzie współrzędnych
plot(skalowanie$points, type = "p", pch=ksztalty, cex=1.5)
# rysujemy również diagram Sheparda
shepard <- MASS::Shepard(niepodobienstwa, skalowanie$points)
plot(shepard, pch = ".")
abline(0,1)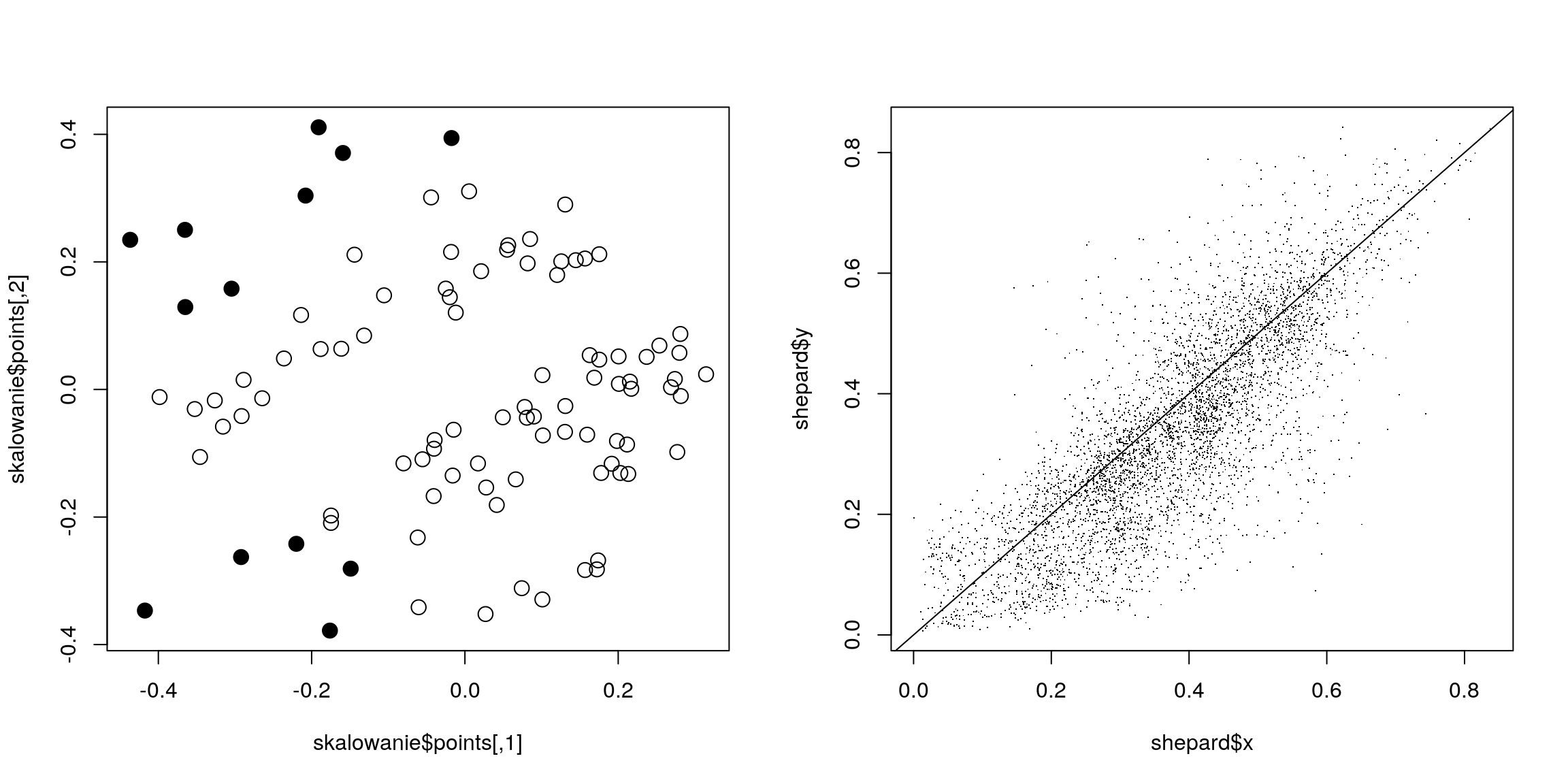

Rysunek 2.5: Graficzna reprezentacja wyników funkcji isoMDS() i Shepard().

Zobaczmy jak wyglądają dane o województwach po przeskalowaniu różnymi metodami. Na wykresie 2.6 po lewej stronie przedstawiamy przeskalowane dane a po prawej wykresy Sheparda.

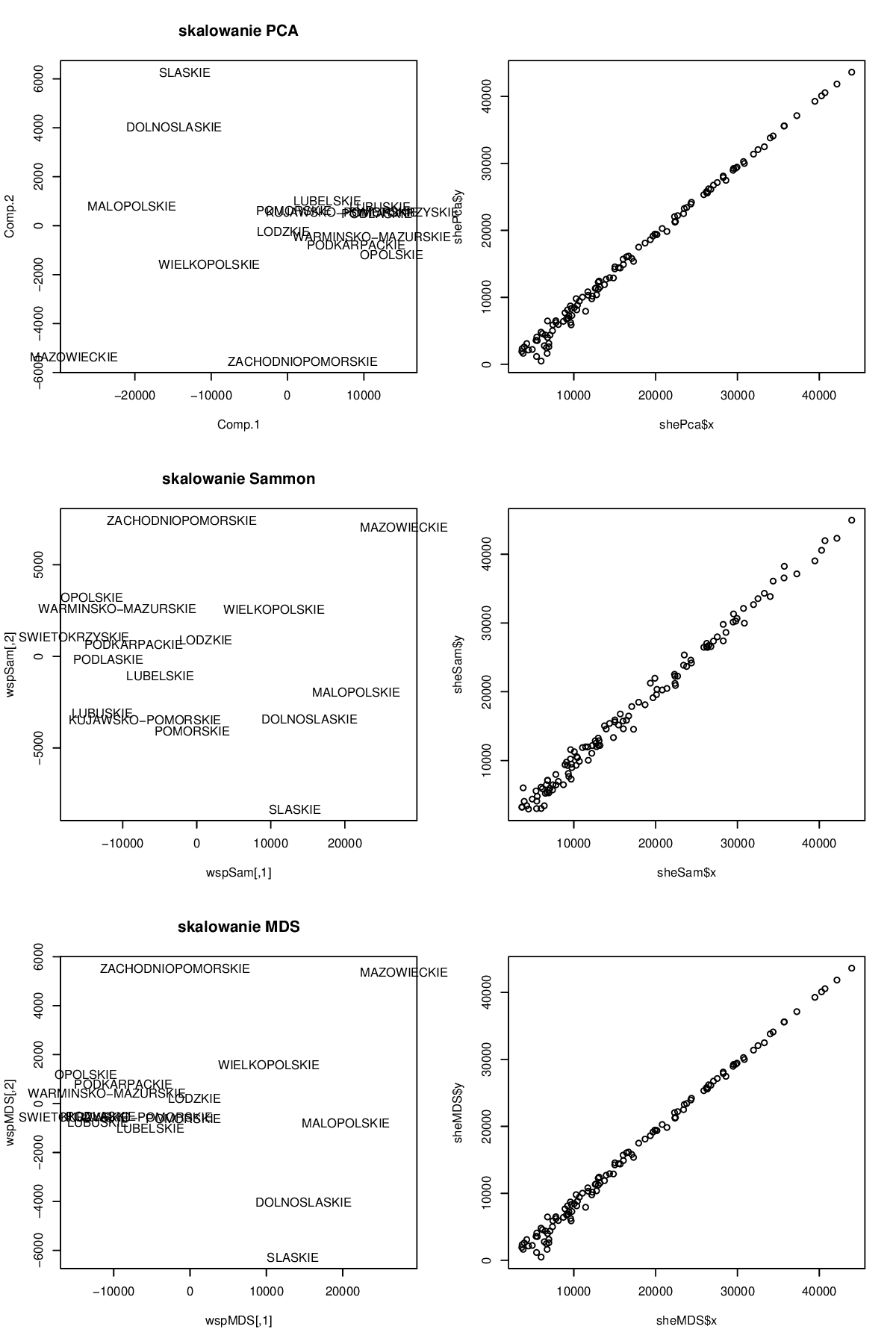
Rysunek 2.6: Graficzna reprezentacja wyników różnych funkcji skalowania, na przykładach danych GUS.

.	opis
\(\texttt{\$points}\)	Macierz współrzędnych obiektów w nowej \(k\)-wymiarowej przestrzeni.
\(\texttt{\$stress}\)	Uzyskana wartość optymalizowanego parametru stresu.

.	opis
\(\texttt{\$sdev}\)	Wektor odchyleń standardowych dla obserwacji. Kolejne zmienne odpowiadają odchyleniom standardowym liczonym dla kolejnych składowych głównych.
\(\texttt{\$rotation}\)	Macierz obrotu przekształcająca oryginalny układ współrzędnych w nowy układ współrzędnych.
\(\texttt{\$center}\)	Wektor wartości wykorzystanych przy centrowaniu obserwacji.
\(\texttt{\$scale}\)	Wektor wartości wykorzystanych przy skalowaniu obserwacji.
\(\texttt{\$x}\)	Macierz współrzędznych kolejnych obserwacji w nowym układzie współrzędnych, macierz ta ma identyczne wymiary co oryginalny zbiór zmiennych.