Rozdział 7 Przykład analizy szeregów czasowych
7.1 Wprowadzenie
W skład szeregu czasowego mogą wchodzić następujące elementy:
trend
deterministyczny
stochastyczny
wahania sezonowe
addytywne
multiplikatywne
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(log(AirPassengers),col="SteelBlue"); title("addytywny")
plot(AirPassengers,col="SteelBlue"); title("multiplikatywwny")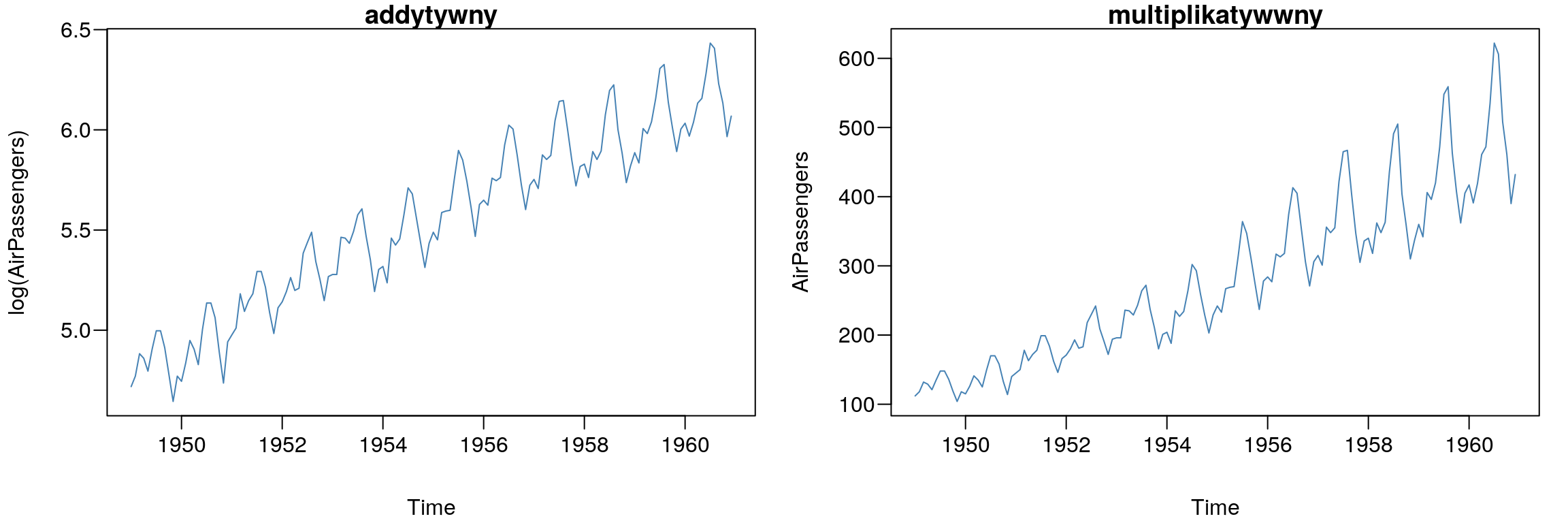
Rysunek 7.1: Przykłady szeregów czasowych.
Wśród szeregów czasowych rozróżniamy dwa rodzaje procesów stochastycznych: stacjonarne (w których nie występuje trend) oraz niestacjonarne (w których występuje trend). Aby wyeliminować tendencję rozwojową z danego procesu można wykorzystać do tego celu różnicowanie:
- jednokrotne różnicowanie:
\[\begin{equation} \Delta y_t=y_t-y_{t-1} \tag{7.1} \end{equation}\]
dy <- diff(AirPassengers)- dwukrotne różnicowanie:
\[\begin{equation} \Delta\Delta y_t=y_t-y_{t-1} \tag{7.2} \end{equation}\]
ddy <- diff(AirPassengers, lag= 1, differences= 2)par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(diff(log(AirPassengers)),col="SteelBlue"); title("addytywny")
plot(diff(AirPassengers),col="SteelBlue"); title("multiplikatywwny")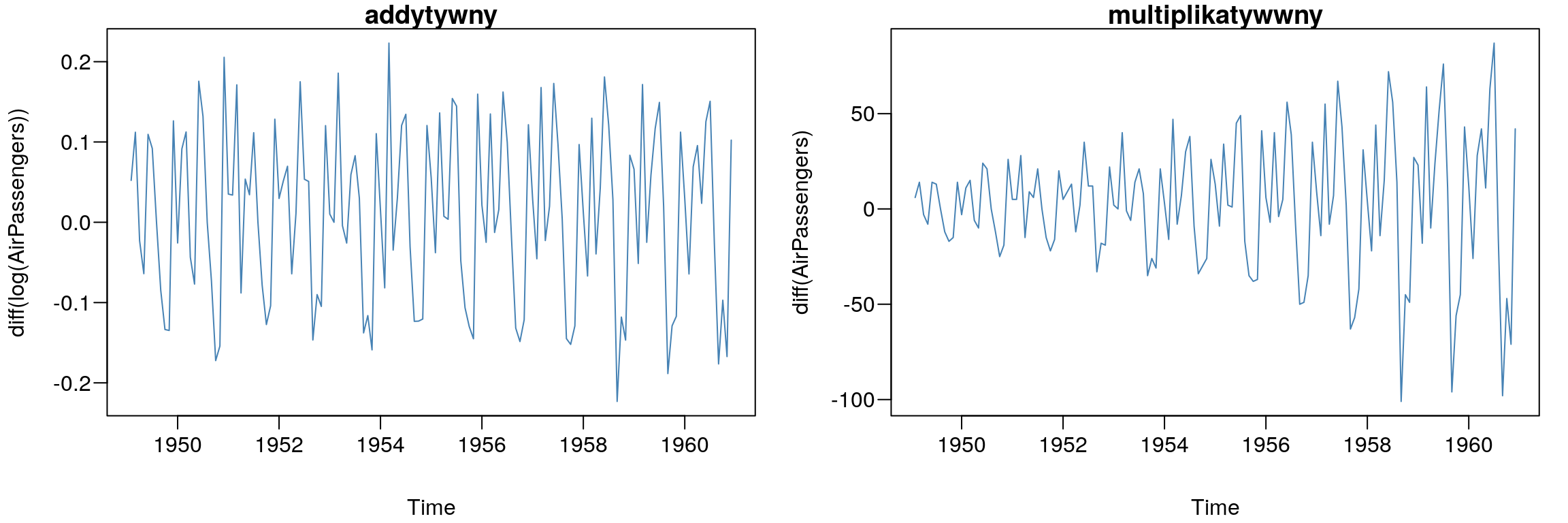
Rysunek 7.2: Przykłady jednokrotnego różnicowania szeregów czasowych.
W środowisku R dostępne są także funkcje dotyczące filtrowania szeregów czasowych. Jest to takie przekształcenie danych które doprowadza do oczyszczenia szeregu czasowego z wahań periodycznych. W środowisku R dostępnych jest kilka takich filtrów. Jeden z bardzie popularnych to filtr Hodrick-Prescotta zaimplementowany w pakiecie FRAPO::trdhp. Stosując filtr HP należy pamiętać o odpowiednim doborze parametru \(\lambda\). Hodrick oraz Prescott zalecają, aby wartość współczynnika \(\lambda\) była równa 400, 1600 i 14400 odpowiednio dla danych rocznych, kwartalnych i miesięcznych.
f <- FRAPO::trdhp(AirPassengers, lambda=14400)
par(mfcol=c(2,1),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(AirPassengers,col="SteelBlue",
main="Hodrick-Prescott filter")
lines(f,col="YellowGreen")
plot(AirPassengers-f,col="SteelBlue",
main="Cyclical component (deviations from trend)")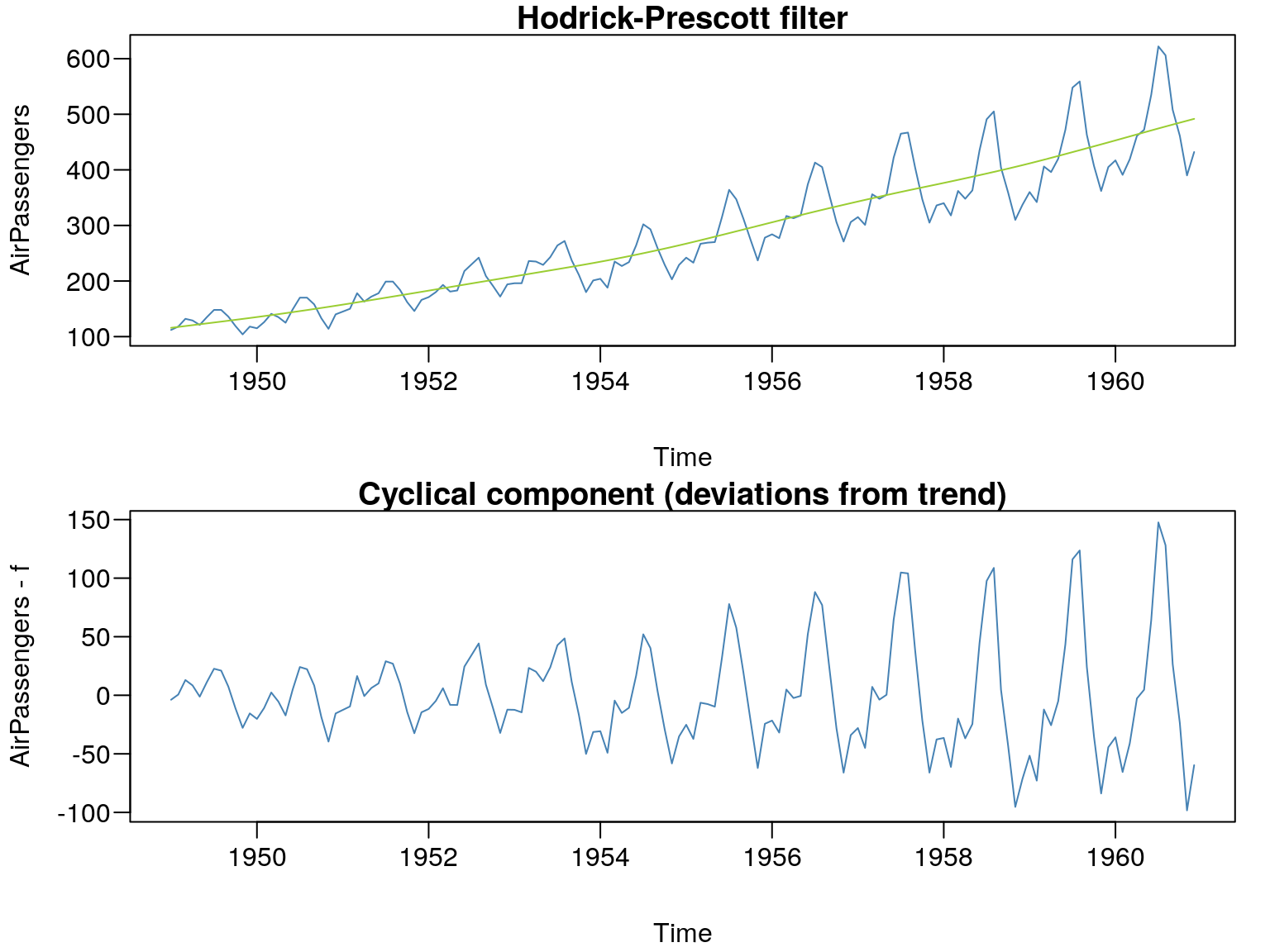
Rysunek 7.3: Filtr Hodrick-Prescott.
Dodajmy, że lepszą alternatywę dla procedury Hodricka-Prescotta zaproponował James D. Hamilton. Ten filtr został zaimplementowany do funkcji neverhpfilter::yth_filter.
7.2 Identyfikacja trendu i sezonowości
7.2.1 Analiza wariancji - ANOVA
Ocena występowania trendu oraz wahań periodycznych zostanie dokonana na przykładzie miesięcznej stopy bezrobocia w Polsce w okresie od 01-2004 do 10-2010 roku.
b <- c(20.6, 20.6, 20.4, 19.9, 19.5, 19.4, 19.3, 19.1, 18.9, 18.7, 18.7, 19.0, 19.4, 19.4,
19.2, 18.7, 18.2, 18.0, 17.9, 17.7, 17.6, 17.3, 17.3, 17.6, 18.0, 18.0, 17.8, 17.2,
16.5, 16.0, 15.7, 15.5, 15.2, 14.9, 14.8, 14.9, 15.1, 14.9, 14.4, 13.7, 13.0, 12.4,
12.2, 11.9, 11.6, 11.3, 11.3, 11.4, 11.7, 11.5, 11.1, 10.5, 10.0, 9.6, 9.40, 9.10,
8.90, 8.80, 9.10, 9.50, 10.5, 10.9, 11.2, 11.0, 10.8, 10.7, 10.8, 10.8, 10.9, 11.1,
11.4, 11.9, 12.7, 13.0, 12.9, 12.3, 11.9, 10.6, 10.7, 11.4, 11.5)
b <- ts(b, frequency = 12, start = c(2004, 1))par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(b,type="l",col="SteelBlue")
Rysunek 7.4: Stopa bezrobocia w Polsce od 01-2004 do 10-2010 roku.
T <- rep(c(2004,2005,2006,2007,2008,2009,2010),c(12,12,12,12,12,12,9))
T <- factor(T)
S <- rep(1:12,7);S=S[-c(82:84)]
S <- factor(S)Identyfikację szeregu czasowego można przeprowadzić na kilka sposobów. Jednym z nich jest analiza wariancji ANOVA.
anova(lm(b~T+S))## Analysis of Variance Table
##
## Response: b
## Df Sum Sq Mean Sq F value Pr(>F)
## T 6 990.99 165.165 523.410 < 2.2e-16 ***
## S 11 51.67 4.697 14.886 1.13e-13 ***
## Residuals 63 19.88 0.316
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Na podstawie przeprowadzonej analizie wariancji, należy stwierdzić, że w omawianym szeregu czasowym występuje trend (p-value = 2.2e-16). W celu dokonania dalszej identyfikacji szeregu (oceny występowania sezonowości) należy wyeliminować tendencję rozwojową (np. poprzez różnicowanie).
anova(lm(diff(b)~T[-1]+S[-1]))## Analysis of Variance Table
##
## Response: diff(b)
## Df Sum Sq Mean Sq F value Pr(>F)
## T[-1] 6 1.7879 0.29798 8.1625 1.617e-06 ***
## S[-1] 11 6.8836 0.62578 17.1420 6.600e-15 ***
## Residuals 62 2.2634 0.03651
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Jednokrotne różnicowanie szeregu nie przyniosło porządanego efektu (p-value = 1.617e-06). Zatem powinniśmy badany szereg poddać dwukrotnemu różnicowaniu. Należy tę procedurę powtarzać, aż do skutku czyli wyeliminowamia trendu.
anova(lm(diff(b,1,2)~T[-c(1,2)]+S[-c(1,2)]))## Analysis of Variance Table
##
## Response: diff(b, 1, 2)
## Df Sum Sq Mean Sq F value Pr(>F)
## T[-c(1, 2)] 6 0.0383 0.00639 0.1030 0.9958
## S[-c(1, 2)] 11 4.3495 0.39541 6.3775 6.621e-07 ***
## Residuals 61 3.7820 0.06200
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dopiero dwukrotne różnicowanie przyniosło porządany efekt (p-value = 0.9958). Tak więc teraz możemy stwierdzić, że w badanym szeregu czasowym występuje sezonowość (p-value = 6.621e-07).
summary(lm(b~T+S))##
## Call:
## lm(formula = b ~ T + S)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.75126 -0.20245 0.02639 0.19755 1.45139
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.75959 0.26044 79.710 < 2e-16 ***
## T2005 -1.31667 0.22933 -5.741 2.91e-07 ***
## T2006 -3.30000 0.22933 -14.390 < 2e-16 ***
## T2007 -6.74167 0.22933 -29.397 < 2e-16 ***
## T2008 -9.57500 0.22933 -41.752 < 2e-16 ***
## T2009 -8.50833 0.22933 -37.101 < 2e-16 ***
## T2010 -7.87546 0.25064 -31.422 < 2e-16 ***
## S2 0.04286 0.30026 0.143 0.886958
## S3 -0.14286 0.30026 -0.476 0.635883
## S4 -0.67143 0.30026 -2.236 0.028894 *
## S5 -1.15714 0.30026 -3.854 0.000275 ***
## S6 -1.61429 0.30026 -5.376 1.18e-06 ***
## S7 -1.71429 0.30026 -5.709 3.29e-07 ***
## S8 -1.78571 0.30026 -5.947 1.31e-07 ***
## S9 -1.91429 0.30026 -6.375 2.42e-08 ***
## S10 -2.16931 0.31386 -6.912 2.85e-09 ***
## S11 -2.08598 0.31386 -6.646 8.23e-09 ***
## S12 -1.80265 0.31386 -5.744 2.88e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5617 on 63 degrees of freedom
## Multiple R-squared: 0.9813, Adjusted R-squared: 0.9762
## F-statistic: 194.4 on 17 and 63 DF, p-value: < 2.2e-16Oszacowane współczynniki regresji liniowej wskazują jakie są różnice między średnimi stapami bezrobocia w poszczególnych latach oraz miesiącach. Punktem referencyjnym dla czynnika T jest 2004 rok, dla S styczeń. Aby zmienić punkt odniesienia np. na rok 2005 wystarczy wykonać komendę:
T = relevel(T, ref="2005")a następnie przeprowadzić regresję. Jeśli chcemy wyznaczyć średnie stopy bezrobocia w poszczególnych latach trzeba skorzystać z funkcji tapply:
tapply(b,T,mean)## 2005 2004 2006 2007 2008 2009 2010
## 18.191667 19.508333 16.208333 12.766667 9.933333 11.000000 11.888889Prezentację graficzną kształtowania się średnich możemy wykonać w następujący sposób:
par(mfcol=c(1,2),mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
interaction.plot(T,S,b,col=1:12,lwd=2)
interaction.plot(S,T,b,col=1:7,lwd=2)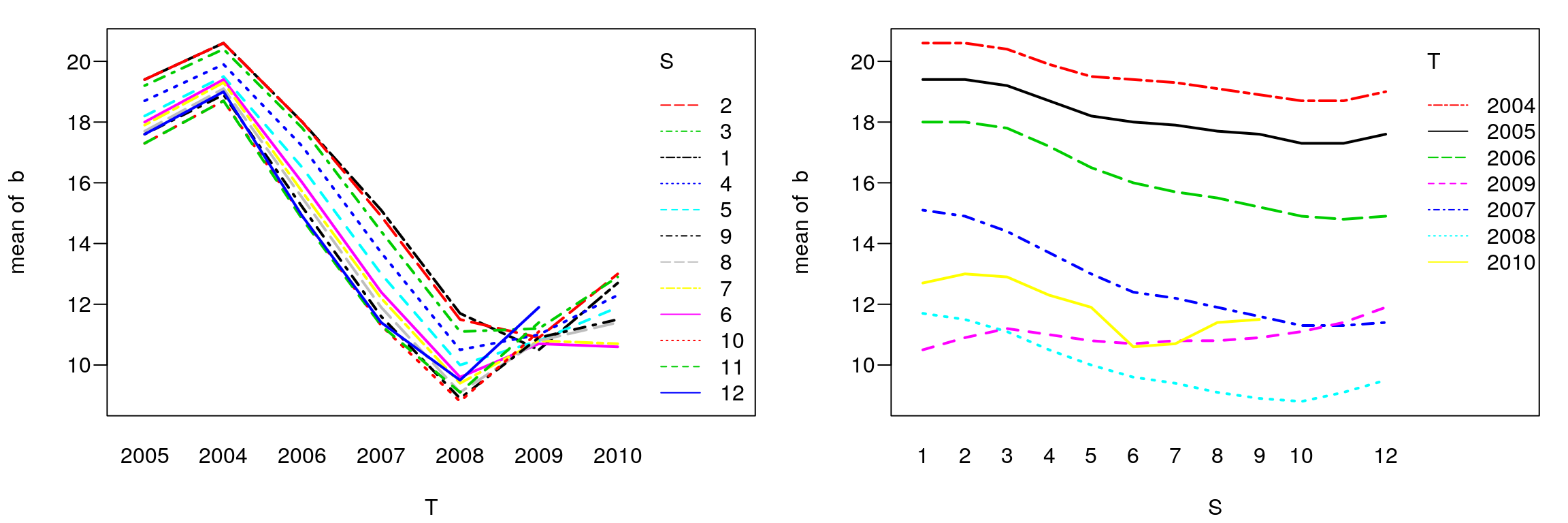
Rysunek 7.5: Średnie dla miesięcy i lat.
7.2.2 Funkcja autokorelacji - ACF
Do identyfikacji składowych szeregu czasowego (trendu oraz sezonowości) można
również wykorzystać funkcję autokorelacji - ACF. W środowisku R jest dostępna
funkcja graficzna forecast::tsdisplay, za pomocą której zostają wygenerowane
trzy wykresy: krzywa badanego zjawiska, funkcja autokorelacji ACF oraz funkcja
częściowej autokorelacji PACF.
forecast::tsdisplay(b,col=2,lwd=2,las=1)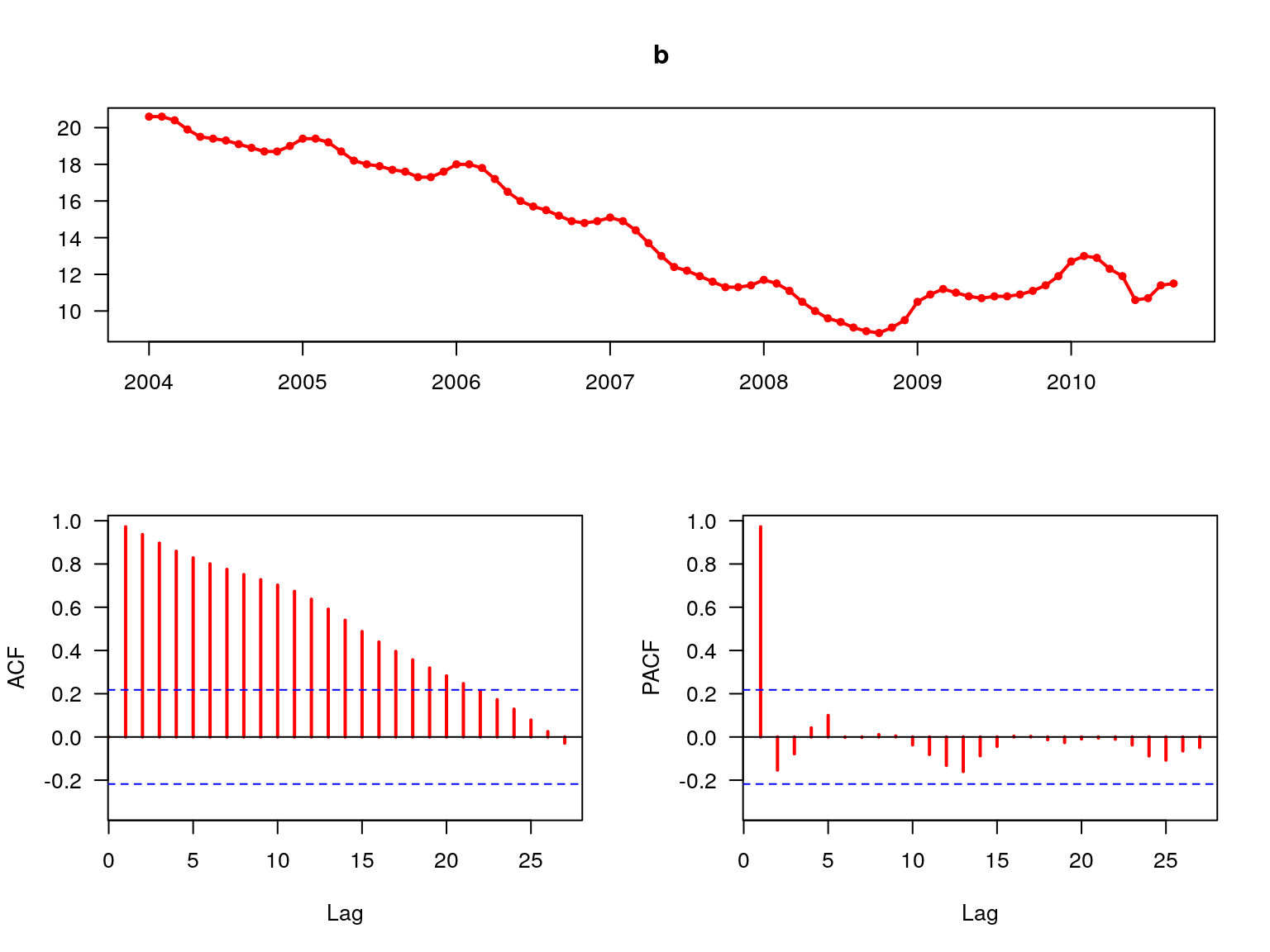
Rysunek 7.6: Funkcja ACF oraz PACF.
Ponieważ funkcja autokorelacji ACF maleje wykładniczo wraz ze wzrostem parametru \(p\) (rys. 7.6) należy sądzić, że w badanym procesie występuje trend.
forecast::tsdisplay(diff(b),col=2,lwd=2,las=1)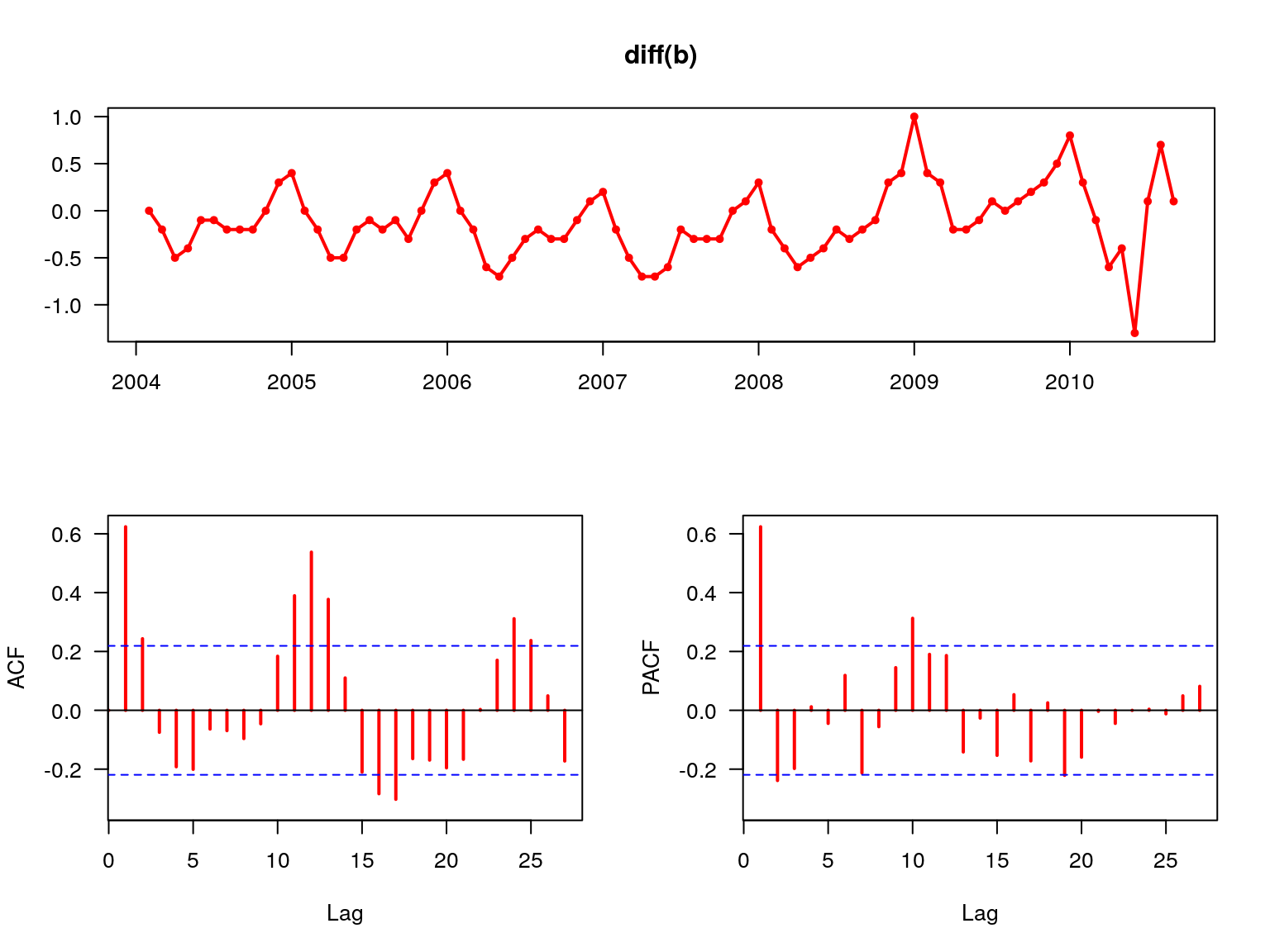
Rysunek 7.7: Funkcja ACF oraz PACF dla pierwszych różnic.
Po zastosowaniu funkcji różnicowania szeregu czasowego trend został wyeliminowany a funkcja ACF wskazuje na występowanie miesięcznych wahań sezonowych (rys. 7.7).
Zatem na podstawie analizy ANOVA oraz funkcji ACF doszliśmy do wniosku,
że badany szereg czasowy charakteryzuje się trendem oraz sezonowością. Również
dzięki funkcji stl za pomocą której dokonaliśmy dekompozycji badanego
procesu (rys. 7.8) możemy potwierdzić występowanie tendencji rozwojowej oraz
wahań periodycznych.
plot(stl(b,s.window="periodic"),col=2,lwd=2)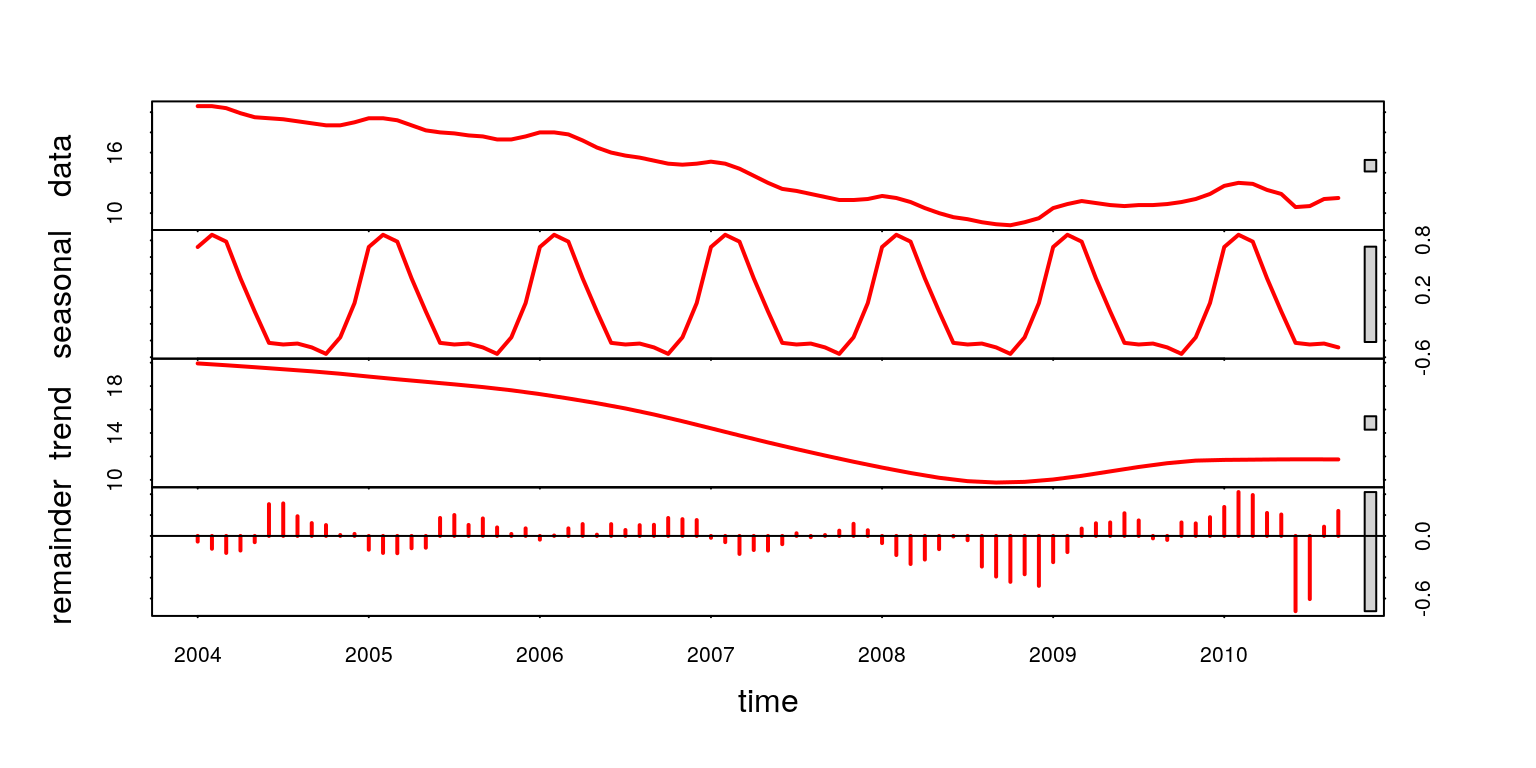
Rysunek 7.8: Dekompozycja szeregu czasowego.
7.3 Modele autoregresyjne ARIMA
Modele \(ARIMA\) służą do analizy stacjonarnych szeregów czasowych. W przypadku gdy szereg jest niestacjonarny należy sprowadzić go do stacjonarności np. poprzez różnicowanie. W skład modelu \(ARIMA(p, d, q)\) mogą wchodzić następujące elementy:
\(AR(p)\) – autoregresja (rząd opóźnienia \(p\))
\(I(d)\) – stopień integracji szeregu (krotność różnicowania \(d\))
\(MA(q)\) – średnia ruchoma (rząd opóźnienia \(q\))
Z kolei gdy w badanym procesie występuje sezonowość należy estymować model o postaci \(SARIMA(p, d, q)(P, D, Q)_m\) gdzie:
\(m\) – sezonowość (np. dla \(m = 4\) sezonowość kwartalna)
\(P\) – autoregresja sezonowa
\(D\) – integracja sezonowa
\(Q\) – średnia ruchoma sezonowa
Prawie każdy model \(ARIMA\) można zapisać w dwojaki sposób np dla procesu \(y_t\):
- \(ARIMA(2,0,0)\) czyli \(AR(2)\):
\[\begin{equation} y_t= \alpha_1 y_{t-1}+\alpha_2 y_{t-2}+\epsilon_t \tag{7.3} \end{equation}\]
- \(ARIMA(2,0,1)\) czyli \(ARMA(2,1)\):
\[\begin{equation} y_t= \alpha_1 y_{t-1}+\alpha_2 y_{t-2}-\beta_1 \epsilon_{t-1}+\epsilon_t \tag{7.4} \end{equation}\]
- \(ARIMA(2,1,0)\) czyli \(ARI(2,1)\):
\[\begin{equation} \Delta y_t= \alpha_1\Delta y_{t-1}+\alpha_2\Delta y_{t-2} +\epsilon_t \tag{7.5} \end{equation}\]
- \(SARIMA(1,0,0)(2,0,0)_4\) czyli \(SARI(1)(2)_4\):
\[\begin{equation} y_t= \alpha_1 y_{t-1}+\alpha_2 y_{t-4}+\alpha_3 y_{t-8} +\epsilon_t \tag{7.6} \end{equation}\]
Środowisko R dostarcza wiele funkcji za pomocą których możemy estymować
modele typu \(ARIMA\). Przykładowo komenda ar daje możliwość estymacji modeli autoregresyjnych \(AR(p)\). Opcja method oferuje kilka sposobów szacowania
parametrów modelu: burg, ols, mle, yule-walker, yw. Z kolei funkcja arima służy do estymacji modeli \(ARIMA\) lub \(SARIMA\). Warto także
zwrócić uwagę na pakiet forecast który dostarcza szereg funkcji do analizy szeregów czasowych.
7.3.1 Estymacja
Wykorzystując funkcje forecast::auto.arima proces estymacji modelu ARIMA
przebiega w sposób całkowicie automatyczny. Spośród wielu estymowanych modeli zostaje wybrany ten, który charakteryzuje się najmniejszą wartością kryterium
informacyjnego AIC – opcja domyślna. W poniższym przykładzie założymy stałą wartość parametru różnicowania \(d=1\).
m <- forecast::auto.arima(b,d=1)
summary(m)## Series: b
## ARIMA(1,1,1)(0,1,0)[12]
##
## Coefficients:
## ar1 ma1
## 0.7948 -0.3710
## s.e. 0.1172 0.1851
##
## sigma^2 estimated as 0.05246: log likelihood=4.58
## AIC=-3.16 AICc=-2.78 BIC=3.5
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set 0.008136148 0.2067496 0.1162358 0.1296337 0.9846707
## MASE ACF1
## Training set 0.05684101 0.02321908Oczywiście można samemu założyć liczbę wszystkich parametrów \(p\), \(d\), \(q\), \(P\) , \(D\), \(Q\).
m <- arima(b,order=c(1,1,0),seasonal=list(order=c(1,0,0),period=12))
summary(m)##
## Call:
## arima(x = b, order = c(1, 1, 0), seasonal = list(order = c(1, 0, 0), period = 12))
##
## Coefficients:
## ar1 sar1
## 0.5580 0.7313
## s.e. 0.0912 0.0834
##
## sigma^2 estimated as 0.04792: log likelihood = 3.24, aic = -0.48
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set -0.007606623 0.2175572 0.1379808 0.02153749 1.097891
## MASE ACF1
## Training set 0.4505497 -0.006360661Warto również zaznaczyć, że w programie R mamy możliwość symulowania procesów autoregresji.
y <- arima.sim( n=1000,
innov=rnorm(1000,0,2), # składnik losowy ma rozkład N(0,2)
model=list(
order = c(2,1,1), # ilość parametrów
ar = c(0.3, 0.6), # wartości parametrów p
ma = c( 0.2), # wartości parametrów q
sd = sqrt(0.1)))par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(ts(y),type="l",col="SteelBlue")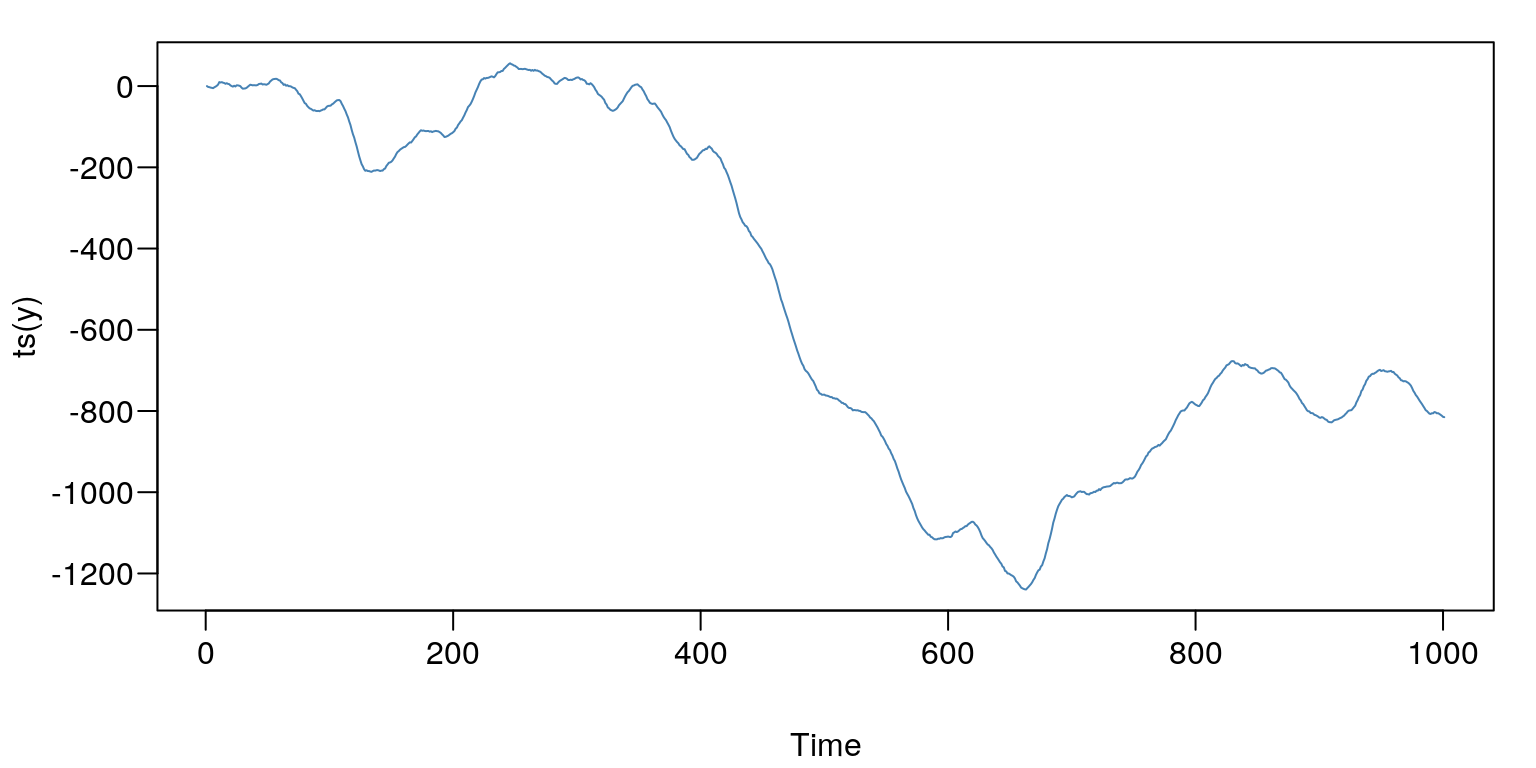
Rysunek 7.9: Prezentacja graficzna symulowanego procesu.
s <- arima(y,order=c(2,1,1))
s##
## Call:
## arima(x = y, order = c(2, 1, 1))
##
## Coefficients:
## ar1 ar2 ma1
## 0.3135 0.5965 0.1721
## s.e. 0.0518 0.0456 0.0643
##
## sigma^2 estimated as 3.776: log likelihood = -2084.28, aic = 4176.57Dzięki zastosowaniu funkcji forecast::ndiffs mamy możliwość sprawdzenia czy rzeczywiście proces y jest zintegrowany w stopniu pierwszym tzn. \(I(1)\). Za pomocą opcji test możemy wybrać procedurę z jakiej chcemy skorzystać: pp – test Phillipsa-Perrona, adf – test Dickeya-Fullera lub kpss – test Kwiatkowski-Phillips-Schmidt-Shin. Poziom istotności alpha także możemy zmieniać.
forecast::ndiffs(y,test="pp",alpha=0.05)## [1] 1Wynikiem funkcji forecast::ndiffs zawsze jest stopień zintegrowania badanego
procesu. Zatem należy stwierdzić, że w zmiennej \(y\) występuje pierwiastek jednostkowy \(d = 1\).
7.3.2 Weryfikacja
Etap weryfikacji oszacowanego modelu \(ARIMA\) polega na sprawdzeniu hipotezy zerowej o braku zjawiska autokorelacji w procesie reszt. Do tego celu możemy wykorzystać test Ljunga-Boxa.
r <- resid(m)
p <- sapply(1:10,function(i) Box.test(r, i, type = "Ljung-Box")$p.value)
p## [1] 0.9535022 0.9152975 0.5318782 0.6333194 0.7667281 0.8522917 0.8863058
## [8] 0.9348725 0.9625130 0.9775571Tak więc na podstawie testu Ljunga-Boxa brak jest podstaw do odrzucenia hipotezy
zerowej zakładającej brak autokorelacji. Wniosek ten potwierdzają również wykresy
wykonane za pomocą komendy tsdiag (rys. 7.10).
par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
tsdiag(m)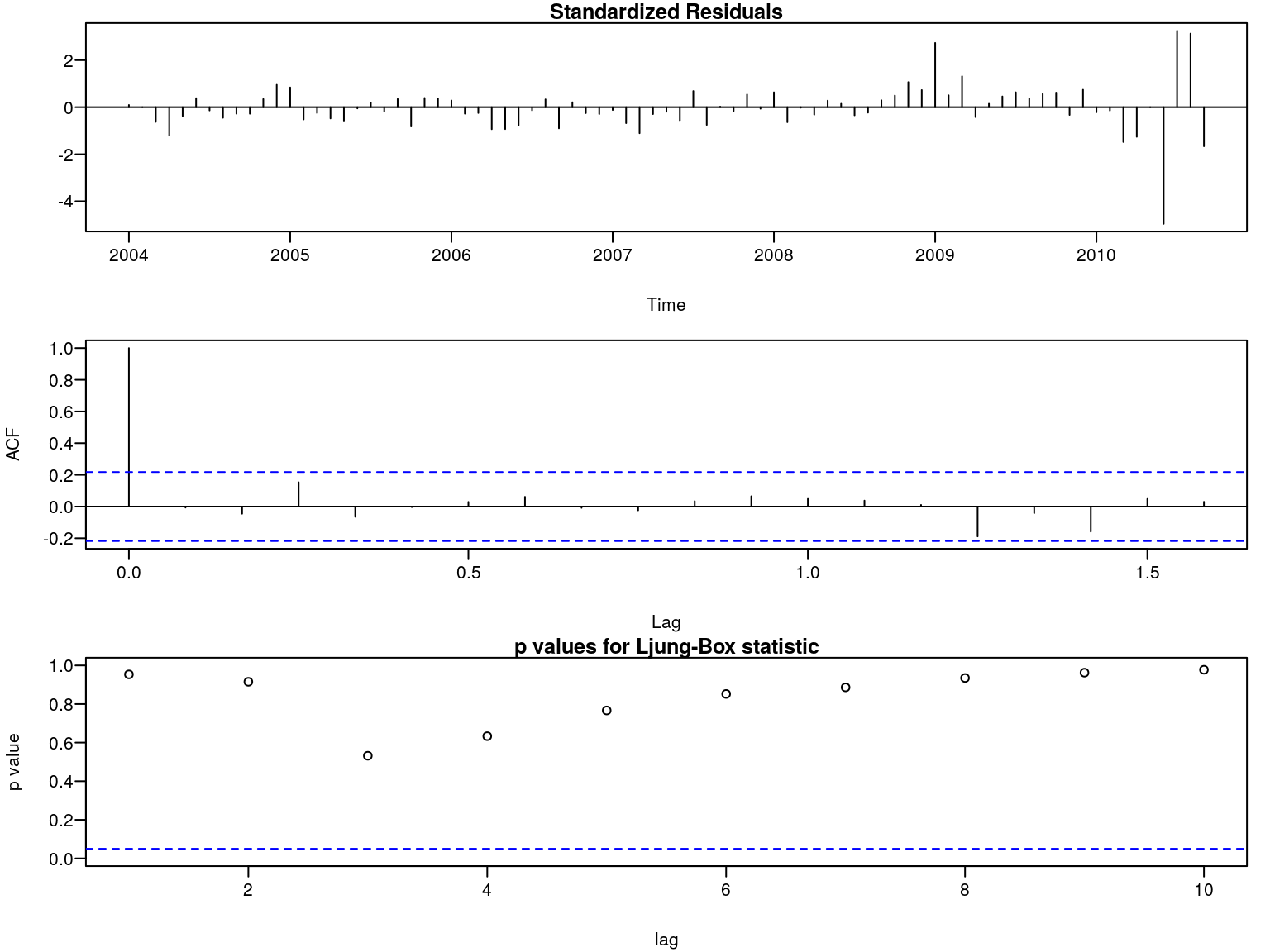
Rysunek 7.10: Diagnostyka reszt modelu.
7.3.3 Prognozowanie
Funkcja forecast::forecast służy do obliczania prognoz na podstawie danego
modelu. W naszym przykładzie liczbę okresów do prognozowania została ustalona
na \(12\) miesięcy. Natomiast przedziały predykcji zostały ustalone na poziomie 80%
i \(95\%\) – są to wartości domyślne. Gdybyśmy chcieli je zmienić na \(99\%\) wystarczy użyć polecenia level=99.
forecast::forecast(m,h=12)## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Oct 2010 11.66125 11.380716 11.94178 11.232211 12.09029
## Nov 2010 11.88899 11.369636 12.40835 11.094703 12.68329
## Dec 2010 12.25929 11.521215 12.99738 11.130499 13.38809
## Jan 2011 12.84691 11.912406 13.78141 11.417711 14.27611
## Feb 2011 13.06774 11.956998 14.17848 11.369006 14.76648
## Mar 2011 12.99543 11.725520 14.26533 11.053272 14.93758
## Apr 2011 12.55712 11.142176 13.97207 10.393148 14.72110
## May 2011 12.26487 10.716515 13.81323 9.896864 14.63288
## Jun 2011 11.31437 9.642230 12.98652 8.757050 13.87170
## Jul 2011 11.38758 9.599679 13.17548 8.653222 14.12194
## Aug 2011 11.89950 10.002628 13.79638 8.998482 14.80053
## Sep 2011 11.97266 9.972585 13.97273 8.913812 15.03150par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(forecast::forecast(m,h=12))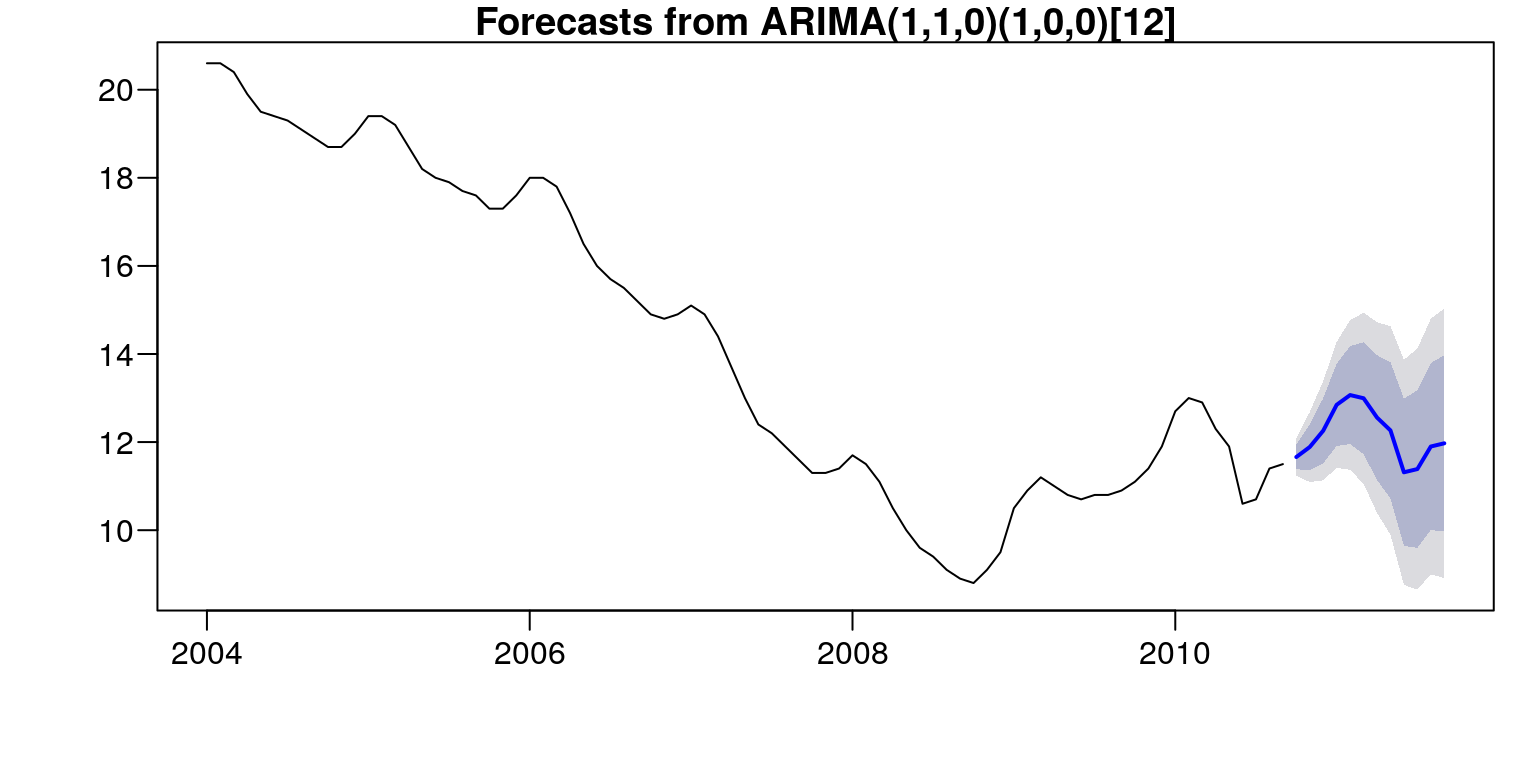
Rysunek 7.11: Prognoza stopy bezrobocia od 10.2010–09.2011.
Dodatkowo możemy wyznaczyć błędy prognoz za pomocą funkcji predict:
p <- predict(m,n.ahead=12)
ts( cbind(pred=p$pred, se=p$se, error=p$se/p$pred), start=c(2010,10),freq=12)## pred se error
## Oct 2010 11.66125 0.2189006 0.01877162
## Nov 2010 11.88899 0.4052582 0.03408683
## Dec 2010 12.25929 0.5759270 0.04697881
## Jan 2011 12.84691 0.7291963 0.05676045
## Feb 2011 13.06774 0.8667176 0.06632497
## Mar 2011 12.99543 0.9909135 0.07625094
## Apr 2011 12.55712 1.1040891 0.08792532
## May 2011 12.26487 1.2081893 0.09850810
## Jun 2011 11.31437 1.3047811 0.11532066
## Jul 2011 11.38758 1.3951054 0.12251115
## Aug 2011 11.89950 1.4801411 0.12438678
## Sep 2011 11.97266 1.5606634 0.13035232Otrzymane wartości prognostyczne wskazują, iż należy się spodziewać wzrostu stopy bezrobocia od października \(2010\)–\(11,66\%\) do lutego 2011–\(13,07\%\). Od marca należy się spodziewać spadku tego wskaźnika do poziomu \(11,31\%\) w czerwcu \(2011\) roku. Następnie będzie on znów powoli wzrastał i w miesiącu wrześniu osiągnie wartość \(11,97\%\). Należy także zwrócic uwagę na oszacowane błędy otrzymanych prognoz. Dla października 2010 wyniósł on \(1,9\%\) i cały czas wzrastał, aż do poziomu \(13,04\%\) dla września \(2011\) roku.
7.4 Modele adaptacyjne
7.4.1 Estymacja
Podobnie jak w przypadku modelu \(ARIMA\) także estymacja modelu adaptacyjnego
może przebiegać w sposób całkowicie automatyczny. Wykorzystamy do tego celu
funkcje forecast::ets.
n <- forecast::ets(b,model="ZZZ",damped=NULL)
summary(n)## ETS(A,Ad,A)
##
## Call:
## forecast::ets(y = b, model = "ZZZ", damped = NULL)
##
## Smoothing parameters:
## alpha = 0.9978
## beta = 0.132
## gamma = 0.0016
## phi = 0.9752
##
## Initial states:
## l = 19.8288
## b = -0.0952
## s = 0.0294 -0.3797 -0.5833 -0.4821 -0.3923 -0.3453
## -0.3235 -0.0403 0.3291 0.7522 0.7916 0.6442
##
## sigma: 0.2251
##
## AIC AICc BIC
## 131.2611 142.2934 174.3612
##
## Training set error measures:
## ME RMSE MAE MPE MAPE
## Training set -0.003431383 0.200049 0.1258755 0.05990526 1.004237
## MASE ACF1
## Training set 0.06155499 0.2850916logLik(n) # logarytm wiarygodności## 'log Lik.' -47.63055 (df=18)Spośród wszystkich modeli, które były estymowane – model="ZZZ" z wykorzystaniem optymalizacji logarytmu wiarygodności – opt.crit="lik", został wybrany
model o najmniejszym kryterium informacyjnym AIC – ic="aic". Dostępne są
także inne metody optymalizacyjne do szacowania parametrów: mse, amse, nmse,
sigma. Także wybór kryterium informacyjnego (za pomocą którego dokonujemy
wyboru najlepszego modelu) możemy wybrać samodzielnie: aic, aicc, bic. Tak
przeprowadzona estymacja doprowadziła do otrzymania modelu "AAdA", który charakteryzuje się następującymi cechami: A – addytywny składnik losowy (pierwsza
litera), Ad – trend addytywny (druga litera), gdzie mała litera d oznacza, że została wybrana również opcja damped=T czyli “przygaszenie” trendu, A – addytywne
wachania sezonowe (trzecia litera). Zatem otrzymaliśmy model Wintersa z addytywnymi wahaniami periodycznymi:
n <- forecast::ets(b, model="AAA")
n## ETS(A,Ad,A)
##
## Call:
## forecast::ets(y = b, model = "AAA")
##
## Smoothing parameters:
## alpha = 0.9978
## beta = 0.132
## gamma = 0.0016
## phi = 0.9752
##
## Initial states:
## l = 19.8288
## b = -0.0952
## s = 0.0294 -0.3797 -0.5833 -0.4821 -0.3923 -0.3453
## -0.3235 -0.0403 0.3291 0.7522 0.7916 0.6442
##
## sigma: 0.2251
##
## AIC AICc BIC
## 131.2611 142.2934 174.3612Oczywiście korzystając z funkcji forecast::ets oraz opcji model możemy od razu zawęzić
grupę modeli, spośród których zostanie wybrany najlepszy z nich: modele Browna
– model="ZNN", modele Browna lub Holta – model="ZZN", modele Browna, Holta
lub Wintersa – model="ZZZ". Jest również możliwość estymacji modeli o ustalonych
parametrach: alpha, beta, gamma, phi. Natomiast gdy ich wartości zawierają się
w pewnych przedziałach liczbowych, przykładowo jeśli \(\alpha = (0,11 - 0,53)\), \(\beta = (0,41 - 0,68)\) i \(\gamma = (0,65 - 0,78)\) to należy użyć opcji level=c(0.11,0.41,0.65) oraz upper=c(0.53,0.68,0.78).
7.4.2 Prognozowanie
Do procesu prognozowania z wykorzystaniem modelu adaptacyjnego możemy również wykorzystać funkcję forecast::forecast.
forecast::forecast(n,h=12)## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Oct 2010 11.45805 11.16963 11.74646 11.016945 11.89914
## Nov 2010 11.71903 11.28458 12.15348 11.054594 12.38346
## Dec 2010 12.18460 11.61967 12.74953 11.320617 13.04858
## Jan 2011 12.85520 12.16506 13.54533 11.799728 13.91066
## Feb 2011 13.05585 12.24227 13.86942 11.811592 14.30010
## Mar 2011 13.06843 12.13164 14.00522 11.635734 14.50113
## Apr 2011 12.69693 11.63640 13.75747 11.074992 14.31888
## May 2011 12.37728 11.19211 13.56246 10.564716 14.18985
## Jun 2011 12.14212 10.83122 13.45302 10.137273 14.14697
## Jul 2011 12.16889 10.73111 13.60667 9.969991 14.36778
## Aug 2011 12.16869 10.60287 13.73452 9.773968 14.56341
## Sep 2011 12.12366 10.42866 13.81867 9.531375 14.71595par(mar=c(4,4,1,1)+0.1, mgp=c(3,0.6,0),las=1)
plot(forecast::forecast(n,h=12))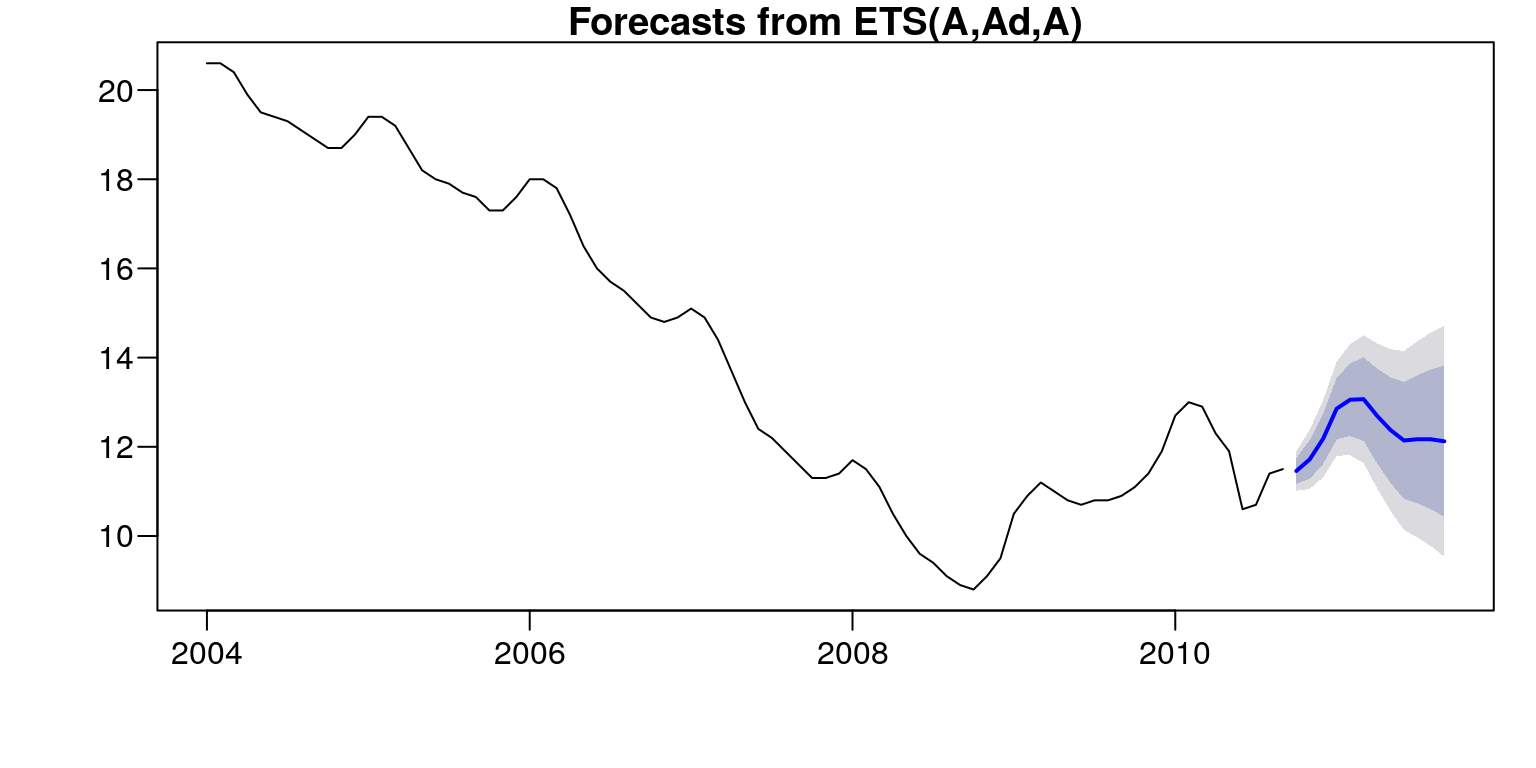
Rysunek 7.12: Prognoza stopy bezrobocia od 10.2010–09.2011.
W przypadku gdy wykonaliśmy dwie prognozy za pomocą różnych modeli (np.
modelu \(ARIMA\) i adaptacyjnego) warto skorzystać z testu Diebold-Mariano. Hipoteza zerowa tego tesu zakłada, że dokładność predykcyjna dwóch modeli jest jednakowa. Założenie alt="two.sided" (test dwustronny) jest opcją domyślną, możemy
ją zmienić dodając polecenie alt="g" (test prawostronny) lub alt="l" (test lewostronny).
forecast::dm.test(resid(m),resid(n))##
## Diebold-Mariano Test
##
## data: resid(m)resid(n)
## DM = 1.0538, Forecast horizon = 1, Loss function power = 2,
## p-value = 0.2951
## alternative hypothesis: two.sided