Rozdział 4 Analiza dyskryminacji

W wielu dziedzinach potrzebne są metody, potrafiące automatycznie przypisać nowy obiekt do jednej z wyróżnionych klas. W medycynie interesować nas może czy pacjent jest chory, a jeżeli tak to na co (zbiorem klas do którego chcemy przypisać mogą być możliwe choroby, lub tylko informacja czy jest chory czy nie). W analizie kredytowej dla firm chcemy przewidzieć czy firma spłaci kredyt czy nie. W analizie obrazów z fotoradarów policyjnych będzie nas interesowało określenie numeru re- jestracji samochodu który przekroczył prędkość a również typu pojazdu (w końcu ograniczenia dla ciężarówek są inne niż dla samochodów).

W rozdziale ?? używaliśmy regresji logistycznej do znalezienia parametrów, które można by wykorzystać w określeniu ryzyka pojawienia się wznowienia choroby u operowanych pacjentek. Okazuje się wiec, że regresja logistyczna jest klasyfikatorem, pozwalającym na przypisanie nowego obiektu do jednej z dwóch klas. Poniżej przedstawimy szereg funkcji implementujących inne popularne metody analizy dyskryminacji.

Celem procesu dyskryminacji (nazywanego też klasyfikacją, uczeniem z nauczycielem lub uczeniem z nadzorem) jest zbudowanie reguły, potrafiącej przypisywać możliwie dokładnie nowe obiekty do znanych klas. W przypadku większości metod możliwe jest klasyfikowanie do więcej niż dwie klasy.

4.1 Dyskryminacja liniowa i kwadratowa

Dyskryminacja liniowa, a więc metoda wyznaczania (hiper)płaszczyzn separujących obiekty różnych klas, jest dostępna w funkcji lda(MASS). Rozszerzeniem tej metody jest dyskryminacja kwadratowa, umożliwiająca dyskryminacje powierzchniami, w opisie których mogą pojawić się człony stopnia drugiego. Metoda klasyfikacji kwadratowej jest dostępna w funkcji qda(MASS). Wynikami obu funkcji jest klasyfikator, wyznaczony na zbiorze uczącym. Aby użyć go do predykcji klas dla nowych obiektów możemy wykorzystać przeciążoną funkcje predict().

Poniżej przedstawiamy przykład użycia funkcji lda(). Z funkcji qda() korzysta się w identyczny sposób. Na potrzeby przykładu wykorzystaliśmy zbiór danych do- tyczących występowania cukrzycy u Indian Pima, ten zbiór danych jest dostępny w zbiorze PimaIndiansDiabetes2(mlbench). Interesować nas będą dwie zmienne z tego zbioru danych, opisujące poziom glukozy i insuliny, w zbiorze danych jest znacznie więcej zmiennych, ale na potrzeby wizualizacji wybraliśmy tę parę. Na bazie tych dwóch zmiennych będziemy badać skuteczność oceny czy dana osoba jest cukrzykiem z wykorzystaniem obu algorytmów klasyfikacji. Zbiór danych podzielimy na dwie części, uczącą i testową. Klasyfikator zostanie „nauczony” na zbiorze uczących, a później będziemy weryfikować jego właściwości na zbiorze testowym. Pierwszym argumentem funkcji lda() jest zbiór zmiennych na bazie których budowany będzie klasyfikator (ramka danych lub macierz). Drugim argumentem grouping jest wektor określający klasy kolejnych obiektów. Kolejnym wykorzystanym poniżej argumentem jest subset, określający indeksy obiektów, na bazie których budowany ma być klasyfikator. Jeżeli argument subset nie będzie podany, to do konstrukcji klasyfikatora wykorzystane będą wszystkie obiekty. Jako pierwszy argument funkcji lda() można również podać również formułę, określającą, które zmienne mają być użyte do konstrukcji klasyfikatora a która zmienna opisuje klasy.

library("mlbench")
# wczytujemy zbiór danych z pakietu mlbench, usuwamy brakujące dane i
# logarytmujemy poziom insuliny
data(PimaIndiansDiabetes2)
dane = na.omit(PimaIndiansDiabetes2)[,c(2,5,9)]
dane[,2] = log(dane[,2])
# zbiór danych chcemy podzielić na dwie części, uczącą i testową,
# funkcją sample wylosujemy indeksy obiektów, które trafia do zbioru uczącego
zbior.uczacy = sample(1:nrow(dane), nrow(dane)/2, FALSE)
# wywołujemy funkcję lda
klasyfikatorLDA = lda(dane[,1:2], grouping = dane[,3], subset=zbior.uczacy)
# jak wygląda wynik w środku?
str(klasyfikatorLDA)

## List of 8
##  $ prior  : Named num [1:2] 0.673 0.327
##   ..- attr(*, "names")= chr [1:2] "neg" "pos"
##  $ counts : Named int [1:2] 132 64
##   ..- attr(*, "names")= chr [1:2] "neg" "pos"
##  $ means  : num [1:2, 1:2] 111.52 145.97 4.64 5.14
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:2] "neg" "pos"
##   .. ..$ : chr [1:2] "glucose" "insulin"
##  $ scaling: num [1:2, 1] 0.0346 0.1268
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:2] "glucose" "insulin"
##   .. ..$ : chr "LD1"
##  $ lev    : chr [1:2] "neg" "pos"
##  $ svd    : num 8.23
##  $ N      : int 196
##  $ call   : language lda(x = dane[, 1:2], grouping = dane[, 3], subset = zbior.uczacy)
##  - attr(*, "class")= chr "lda"

Zbudowanie klasyfikatora to dopiero pierwszy krok, kolejnym jest jego ocena. Na bazie obserwacji niewykorzystanych do budowania klasyfikatora zbadamy jaka była zgodność klasyfikatora z rzeczywistymi danymi (ponieważ zbiór uczący wybraliśmy losowo, to dla różnych powtórzeń otrzymalibyśmy inny błąd klasyfikacji). Do klasyfikacji nowych obiektów użyjemy funkcji predict(). Jest to funkcja przeciążona, działająca dla większości klasyfikatorów. Wynikiem tej funkcji mogą być prognozowane klasy dla nowych obserwacji, lub też prawdopodobieństwa a posteriori przynależności do danej klasy.

# używając metody predict wykonujemy klasyfikacje obiektów ze zbioru testowego
oceny = predict(klasyfikatorLDA, newdata=dane[-zbior.uczacy,1:2])
# jak wyglądają wyniki? Pole $class wskazuje na przewidzianą klasę, pole
# $posterior określa wyznaczone prawdopodobieństwo przynależności do
# każdej z klas, na podstawie tej wartości obiekt był przypisywany do
# bardziej prawdopodobnej dla niego klasy
str(oceny)

## List of 3
##  $ class    : Factor w/ 2 levels "neg","pos": 1 2 1 1 1 1 1 2 1 2 ...
##  $ posterior: num [1:196, 1:2] 0.952 0.282 0.751 0.871 0.797 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:196] "7" "15" "17" "19" ...
##   .. ..$ : chr [1:2] "neg" "pos"
##  $ x        : num [1:196, 1] -1.5878 1.5405 -0.0836 -0.7312 -0.2981 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:196] "7" "15" "17" "19" ...
##   .. ..$ : chr "LD1"

# porównajmy macierzą kontyngencji oceny i rzeczywiste etykietki dla kolejnych obiektów
table(predykcja = oceny$class, prawdziwe = dane[-zbior.uczacy,3])

##          prawdziwe
## predykcja neg pos
##       neg 118  32
##       pos  12  34

W powyższym przykładzie w ostatnim poleceniu wyznaczyliśmy tablice kontyngencji dla wyników. Na bazie tak otrzymanej tablicy kontyngencji można wyznaczyć błąd predykcji. Jest wiele wskaźników opisujących błąd predykcji, począwszy od popularnych: czułość (ang. sensitivity TP/(TP+FN) opisuje jaki procent chorych zostanie poprawnie zdiagnozowanych jako chorzy), specyficzność (ang. (Specifity) TN/(TN+FP) określa jaki procent zdrowych zostanie poprawnie zdiagnozowanych jako zdrowi), przez mniej popularne aż po takie o których mało kto słyszał (np. mutual information, współczynnik \(\phi\) itp.). Bogata lista takich współczynników wymieniona jest w opisie funkcji performance(ROCR) (definiując błąd klasyfikacji używa się oznaczeń TP, TN, FP, FN określających kolejno liczbę poprawnie wykrytych sygnałów pozytywnych, poprawnie wykrytych braków sygnału, fałszywie wykrytych sygnałów pozytywnych oraz fałszywie wykrytych braków sygnałów. W powyższym przypadku czułość wyniosła \(31/(31+29)\approx0,517\) a specyficzność \(115/(115+21)\approx 0,846\).

Jeżeli już jesteśmy przy pakiecie ROCR to na przykładzie przedstawimy w jaki sposób wyznaczać krzywe ROC dla klasyfikatorów. Proszę zauważyć, że funkcja predict() poza ocenionymi klasami jako wynik przekazuje również prawdopodobieństwo przynależności do jednej z klas (pole posterior wyniku funkcji predict()). Krzywa ROC to zbiór punktów wyznaczonych dla różnych poziomów odcięcia (ang. threshold) dla wspomnianego prawdopodobieństwa przynależności do jednej z klas. Współrzędne każdego punktu to czułość i specyficzność (dokładniej rzecz biorąc 1-specyficzność) otrzymana dla zadanego punktu odcięcia.

Poniżej przykład użycia funkcji z pakietu ROCR, służącej do rysowania krzywych ROC i innych o podobnych właściwościach. Wynik graficzny przedstawiony jest na rysunku 4.1. Na osiach tego wykresu mogą być przedstawiane różne miary dokładności klasyfikacji, w zależności od argumentów funkcji performance().

# wyznaczamy obiekt klasy prediction, zawierający informacje o prawdziwych
# klasach, i prawdopodobieństwu przynależności do wybranej klasy
pred <- ROCR::prediction(oceny$posterior[,2], dane[-zbior.uczacy,3])
# wyznaczamy i wyrysowujemy wybrane miary dobroci klasyfikacji
perf <- ROCR::performance(pred, "sens", "spec")
par(mfcol=c(1,2))
plot(perf@x.values[[1]], perf@y.values[[1]],type="l")
perf <- ROCR::performance(pred, "prec", "rec")
plot(perf@x.values[[1]], perf@y.values[[1]],type="l")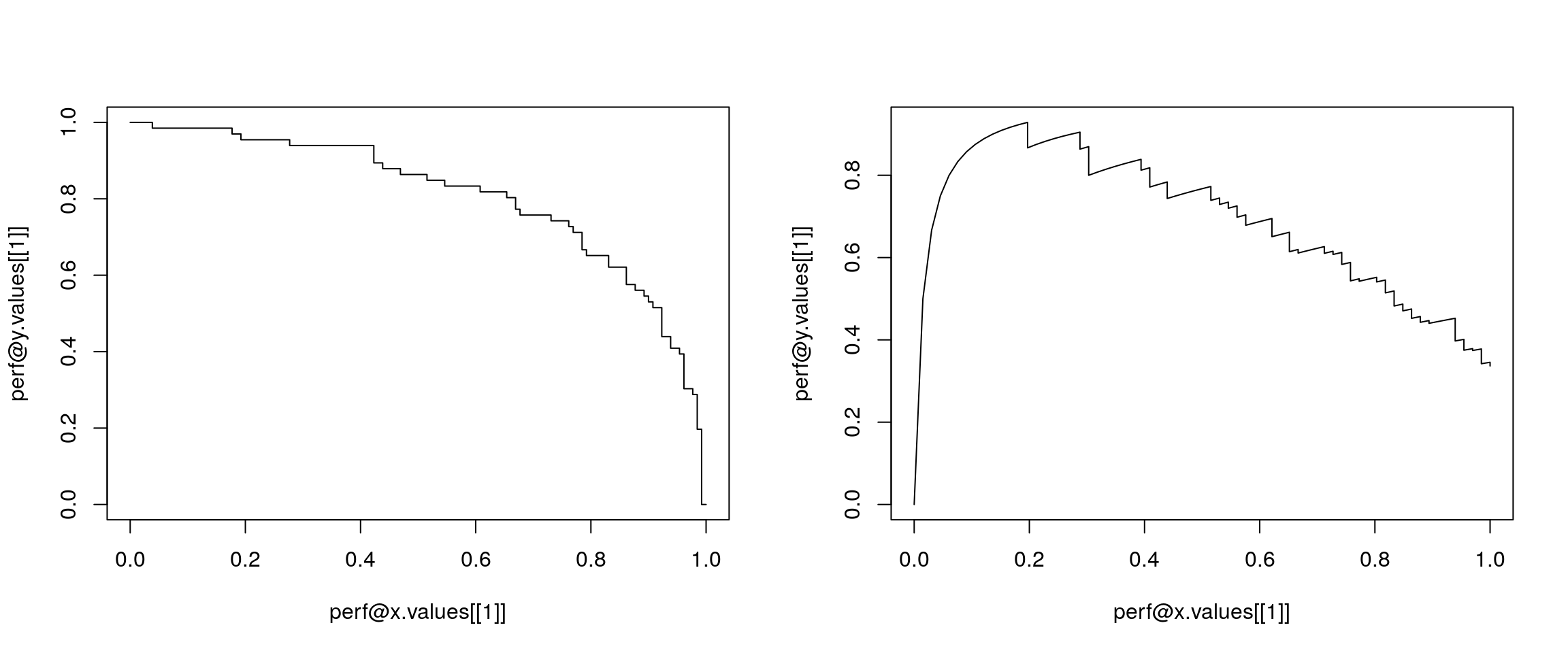

Rysunek 4.1: Wykres zależności czułości od specyficzności oraz miary prediction od recall dla klasyfikacji z użyciem funkcji lda().

Na rysunku 4.2 przedstawiamy kształty obszarów decyzyjnych dla obu klasyfikatorów (do wyznaczania obszarów decyzyjnych można się posłużyć funkcją partimat(klaR) lub drawparti(klaR)). Obszary decyzyjne wyznaczane są dla wytrenowanego klasyfikatora, przedstawiają do której klasy zostałby przypisany punkt o określonych współrzędnych. Osoby chore na cukrzyce oznaczane są czarnymi krzyżykami, osoby zdrowe czerwonymi okręgami. Punkty w których przewidzianą klasą była by cukrzyca zaznaczone są ciemnoszarym kolorem a punkty dla których klasyfikowalibyśmy do grona osób zdrowych zaznaczono jaśniejszym szarym kolorem.

PimaIndiansDiabetes2 = na.omit(PimaIndiansDiabetes2)
dat = PimaIndiansDiabetes2[,c(2,5)]
dat[,2] = log(dat[,2])

colnames(dat) =  c("glucose", "log(insulin)")
klasa = as.numeric(PimaIndiansDiabetes2$diabetes)

seqx = seq(30,210,2)
seqy = seq(2.5,7,0.07)
siata = as.data.frame(expand.grid(seqx, seqy))
colnames(siata) =c("glucose", "log(insulin)")

kol  = c("grey90", "grey70")
kol2  = c("red", "black")
par(mfcol=c(1,2))
klasyfikatorLDA = MASS::lda(dat, klasa)
wub = predict(klasyfikatorLDA, newdata=siata)

plot(siata, col=kol[as.numeric(wub$class)],
     pch=15,xlim=range(dat[,1]),ylim=range(dat[,2]), main="lda()")
points(dat,pch=c(1,4)[klasa], cex=1, col=kol2[klasa], lwd=2)

klasyfikatorLDA = MASS::qda(dat, klasa)
wub = predict(klasyfikatorLDA, newdata=siata)

plot(siata, col=kol[as.numeric(wub$class)],
     pch=15,xlim=range(dat[,1]),ylim=range(dat[,2]), main="qda()")
points(dat,pch=c(1,4)[klasa], cex=1, col=kol2[klasa], lwd=2)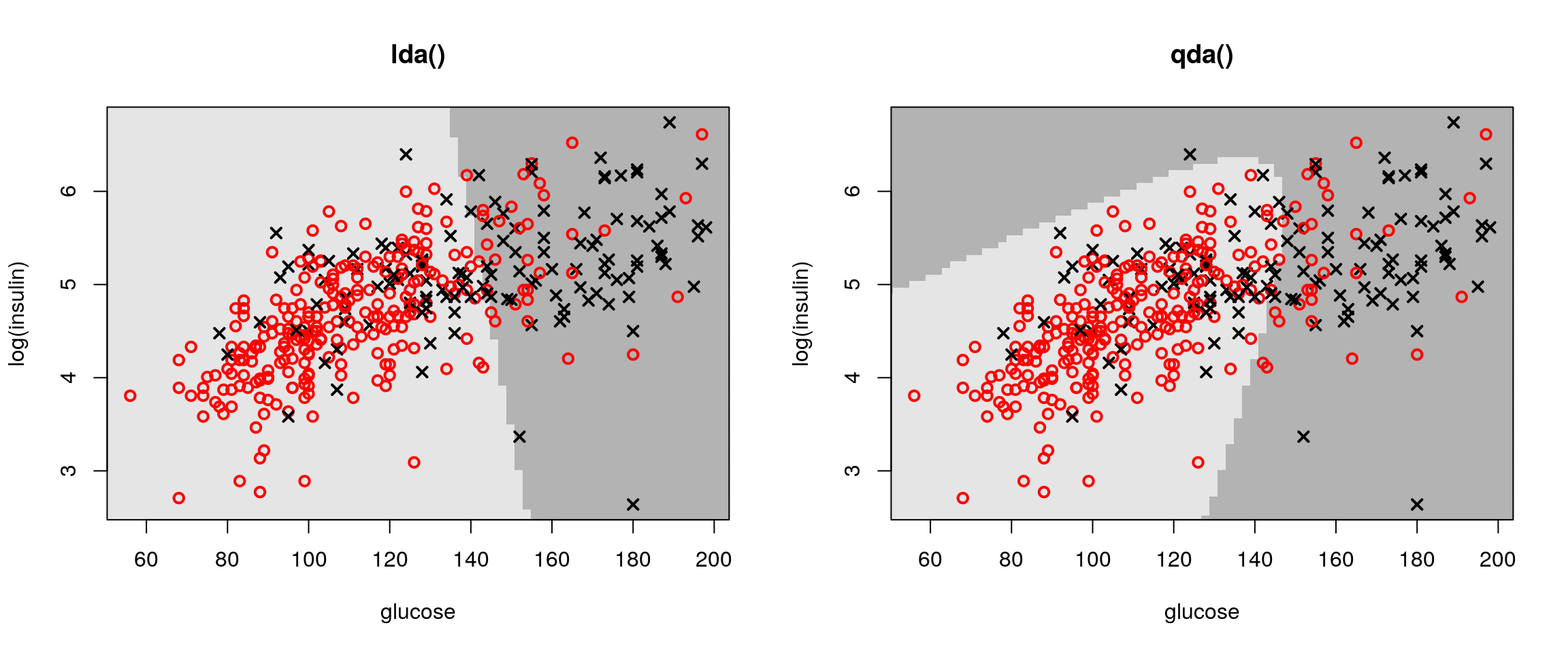

Rysunek 4.2: Przykładowe obszary decyzyjne dla liniowej i kwadratowej dyskryminacji dostępne w funkcjach lda() o qda().

4.2 Metoda najbliższych sąsiadów

Bardzo popularną metodą klasyfikacji jest metoda k-sąsiadów. Idea jej działania jest prosta i intuicyjna. Nowemu obiektowi przypisuje się klasę, która występuje najczęściej wśród jego k sąsiadów (k najbliższych obiektów znajdujących się w zbiorze uczącym, najbliższych w sensie określonej miary odległości). Ten klasyfikator dostępny jest w różnych funkcjach, począwszy od knn(class) (zwykły klasyfikator najbliższych sąsiadów), przez kknn(kknn) (ważony klasyfikator k-sąsiadów) oraz knncat(knncat) (klasyfikator k-sąsiadów, również dla zmiennych jakościowych). Poniżej przedstawimy implementację metody k-sąsiadów z funkcji ipredknn(ipred). Na rysunku 4.3 prezentujemy obszary decyzyjne wyznaczone dla różnej liczby sąsiadów (odpowiednio k=3 i k=21) w omawianym zagadnieniu klasyfikacji na osoby zdrowe i chore na cukrzycę. Ponieważ metoda k-sąsiadów bazuje silnie na odległościach pomiędzy obiektami (jakoś trzeba mierzyć odległość od sąsiadów), przed rozpoczęciem obliczeń wykonamy skalowanie danych.

# zaczynamy od przeskalownia danych
dane[,1:2] = scale(dane[,1:2])
# budujemy klasyfikator k-sąsiadów, dla 3 sąsiadów
klasyfikatorKNN = ipred::ipredknn(diabetes~glucose+insulin, 
                                  data = dane, subset=zbior.uczacy, k=3)
# wykonujemy predykcję klas i wyświetlamy macierz kontyngencji
oceny = predict(klasyfikatorKNN, dane[-zbior.uczacy, ], "class")
table(predykcja = oceny, prawdziwe = dane[-zbior.uczacy,3])

##          prawdziwe
## predykcja neg pos
##       neg 102  32
##       pos  28  34

Błąd klasyfikacji można liczyć na palcach (powyższą procedurę należało by uśrednić po kilku wstępnych podziałach na zbiór uczący i testowy). Można też błąd klasyfikacji wyznaczyć wykorzystać funkcję errorest(ipred). Wylicza ona błąd klasyfikacji (okeślony jako procent źle zaklasyfikowanych obiektów) używając różnych estymatorów tego błędu, w tym opartego na walidacji skrośnej (ocenie krzyżowej, ang. cross validation, domyślnie z podziałem na 10 grup), metodzie bootstrap lub estymatorze 632+. Estymator błędu możemy wybrać określając argument estimator. W funkcji errorest() jako kolejne argumenty należy wskazać zbiór danych, metodę budowy klasyfikatora (argument model) oraz metodę wyznaczania ocen dla zbioru testowego (argument predict). Funkcja errorest() pozwala na jednolity sposób wyznaczenia błędu dla dowolnej metody klasyfikacji. Przedstawimy poniżej przykład dla metody najbliższych sąsiadów.

# wyznaczmy błąd klasyfikacji dla metody 3 sąsiadów
ipred::errorest(diabetes~glucose+insulin, data = dane, model=ipred::ipredknn, k=3,
                estimator = "632plus",
                predict= function(ob, newdata) predict(ob, newdata, "class"))

## 
## Call:
## errorest.data.frame(formula = diabetes ~ glucose + insulin, data = dane, 
##     model = ipred::ipredknn, predict = function(ob, newdata) predict(ob, 
##         newdata, "class"), estimator = "632plus", k = 3)
## 
##   .632+ Bootstrap estimator of misclassification error 
##   with 25 bootstrap replications
## 
## Misclassification error:  0.2896

# wyznaczmy błąd klasyfikacji dla metody 21 sąsiadów, powinna być stabilniejsza
blad = ipred::errorest(diabetes~glucose+insulin, data = dane, model=ipred::ipredknn, k=21,
                estimator = "632plus",
                predict= function(ob, newdata) predict(ob, newdata, "class"))
blad$error

## [1] 0.254772

dane[,1:2]=scale(dane[,1:2])
seqx = seq(-2.7,2.7,0.09)
seqy = seq(-3.2,3.2,0.09)
siata = as.data.frame(expand.grid(seqx, seqy))
colnames(siata) = colnames(dane[,1:2])

par(mfrow=c(1,2))

klasyfikatorKNN = ipred::ipredknn(diabetes~glucose+insulin, 
                                  data = dane, subset=zbior.uczacy, k=3)
#predict(klasyfikatorKNN, dane[-zbior.uczacy, ], "class")
wub = predict(klasyfikatorKNN, newdata=siata, "class")
plot(siata, col=kol[as.numeric(wub)], pch=15, main="ipredknn(, k=3)",
     ylim=c(-3,3),xlim=c(-2.5,2.5))
points(dane[,1:2],pch=c(1,4)[as.numeric(dane[,3])], cex=1,
       col=kol2[as.numeric(dane[,3])], lwd=2)

klasyfikatorKNN = ipred::ipredknn(diabetes~glucose+insulin, 
                                  data = dane, subset=zbior.uczacy, k=21)
#predict(klasyfikatorKNN, dane[-zbior.uczacy, ], "class")
wub = predict(klasyfikatorKNN, newdata=siata, "class")
plot(siata, col=kol[as.numeric(wub)], pch=15, main="ipredknn(, k=21)",
     xlim=c(-2.5,2.5),ylim=c(-3,3))
points(dane[,1:2],pch=c(1,4)[as.numeric(dane[,3])], cex=1, 
       col=kol2[as.numeric(dane[,3])], lwd=2)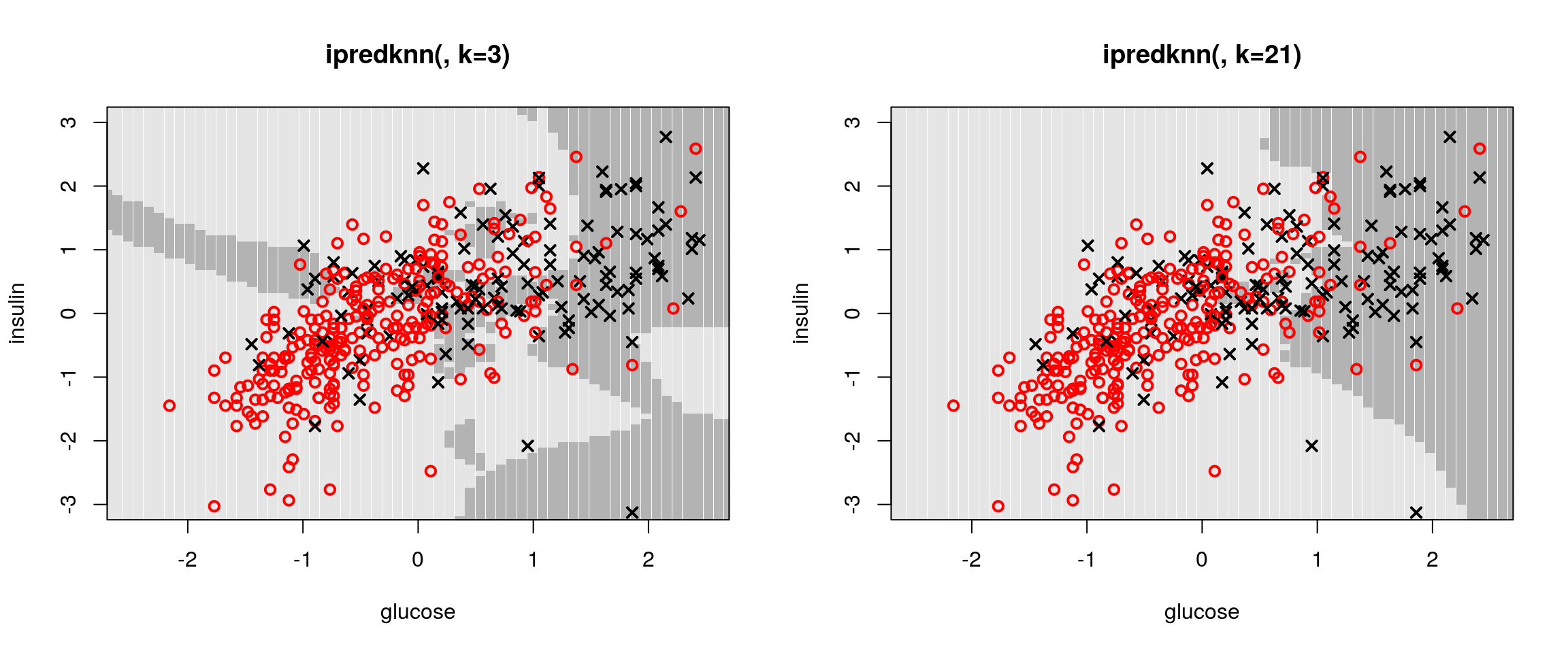

Rysunek 4.3: Przykładowe obszary decyzyjne dla metody k-sąsiadów z parametrami k=3 i k=21.

4.3 Naiwny klasyfikator Bayesowski

Do klasyfikacji wykorzystać można szeroką grupę metod bazujących na ocenie prawdopodobieństwa przynależności do określonej grupy. Dla każdej z klas ocenia się częstość (w przypadku ciągłym gęstość) występowania obiektów o określonych parametrach. Następnie dla nowego obiektu wyznacza się częstości występowania obiektów poszczególnych klas i wybiera się klasę występującą dla tych parametrów najczęściej.

Do tej grupy metod należy naiwny klasyfikator Bayesowski. Bayesowski, ponieważ bazuje na regule Bayesa użytej do wyznaczenia prawdopodobieństwa a posteriori należenia do poszczególnych klas. Naiwność w tym kontekście oznacza przyjęte założenie, że łączna gęstość występowania obiektów jest iloczynem gęstości brzegowych. Naiwny klasyfikator Bayesowski jest dostępny w funkcjach naiveBayes(e1071) i NaiveBayes(klaR). Poniżej przedstawimy tą drugą implementację. Sposób użycia tej funkcji jest podobny do użycia innych opisanych powyżej klasyfikatorów. Na rysunku 4.4 przestawione są warunkowe brzegowe oceny gęstości dla obu zmiennych dla każdej z klas, na bazie tych gęstości wykonywana jest kalsyfikacja. Na rysunku 4.5 przedstawiamy przykładowe obszary decyzyjne dla naiwnego klasyfikatora Bayesowskiego.

# konstruujemy naiwny klasyfikator Bayesowski
mN <- klaR::NaiveBayes(diabetes~glucose+insulin, data=dane, subset=zbior.uczacy)
# wyznaczamy oceny
oceny <- predict(mN, dane[-zbior.uczacy,])$class
table(predykcja = oceny, prawdziwe = dane[-zbior.uczacy,3])

##          prawdziwe
## predykcja neg pos
##       neg 114  30
##       pos  16  36

par(mfcol=c(1,2))
plot(mN)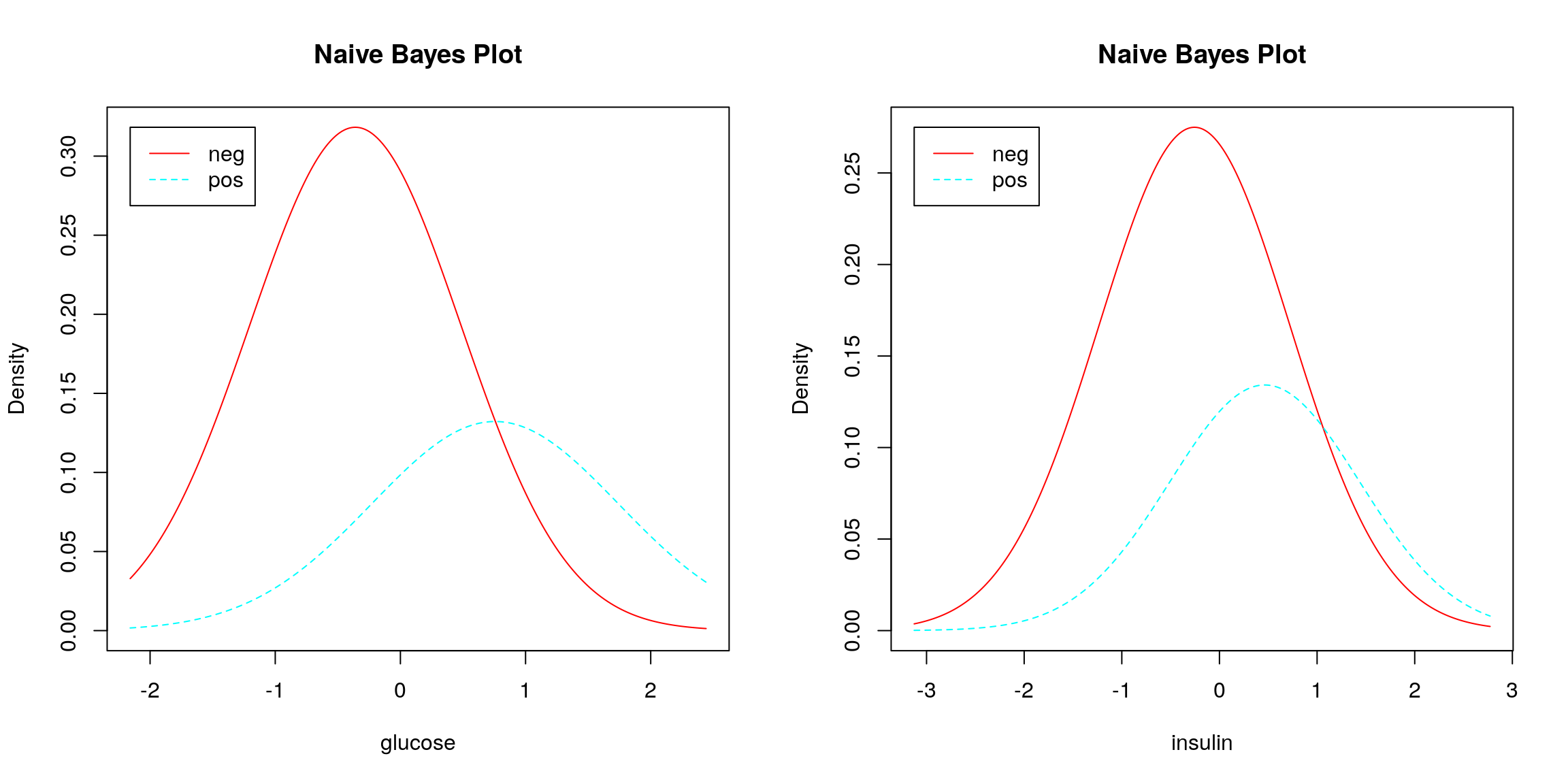

Rysunek 4.4: Warunkowe brzegowe oceny gęstości, na ich bazie funkcjonuje naiwny klasyfikator Bayesowski.

PimaIndiansDiabetes2 = na.omit(PimaIndiansDiabetes2)
dane = PimaIndiansDiabetes2[,c(2,5,9)]
dane[,2] = log(dane[,2])

seqx = seq(30,210,2)
seqy = seq(2.5,7,0.07)
siata = as.data.frame(expand.grid(seqx, seqy))

kol  = c("grey90", "grey70")
klasyfikatorKNN = klaR::NaiveBayes(diabetes~glucose+insulin, data = dane)
wub = predict(klasyfikatorKNN, newdata=siata)$class
plot(siata, col=kol[as.numeric(wub)], pch=15, main="NaiveBayes()", 
     xlab="insulin",ylab="glucose", xlim=range(dat[,1]),ylim=range(dat[,2]))
points(dane[,1:2],pch=c(1,4)[as.numeric(dane[,3])], cex=1, 
       col=kol2[as.numeric(dane[,3])], lwd=2)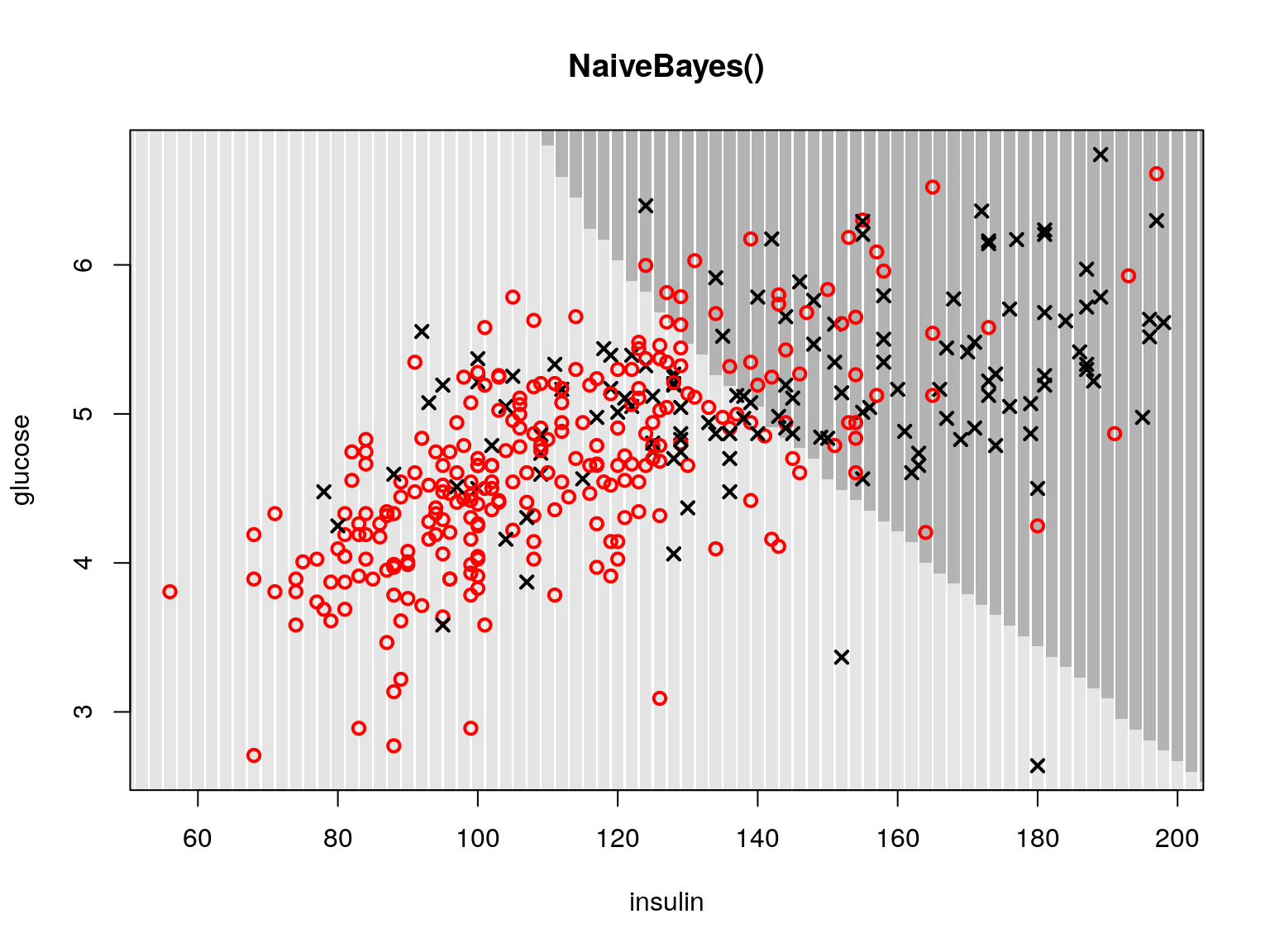

Rysunek 4.5: Przykładowe obszary decyzyjne dla naiwnego klasyfikatora Bayesowskiego.

4.4 Drzewa decyzyjne

Inną klasą klasyfikatorów są cieszące się dużą popularnością metody bazujące na drzewach decyzyjnych (klasyfikacyjnych). W tym przypadku klasyfikator jest reprezentowany przez drzewo binarne, w którego węzłach znajdują się pytania o wartości określonej cechy, a w liściach znajdują się oceny klas. Przykład drzewa klasyfikacyjnego przedstawiamy na rysunku 4.6. Dodatkowo w liściach przedstawiono proporcję obiektów z obu klas, które znalazły się w danym węźle, a wiec spełniły warunki określone w poszczególnych węzłach drzewa. Jeżeli nowe obiekty będziemy przypisywać do klasy, która w danym liściu występowała najczęściej, to dla trzech liści (czwartego, szóstego i siódmego) klasyfikować będziemy do grupy osób chorych, a w pozostałych liściach będziemy klasyfikować do grupy osób zdrowych.

W pakiecie R metoda wyznaczania drzew decyzyjnych dostępna jest w wielu różnych funkcjach. Popularnie wykorzystywane są funkcje tree(tree), rpart(rpart) oraz cpart(party). Poniżej przedstawimy tylko tą ostatnią, ponieważ są dla niej opracowane najbardziej atrakcyjne funkcje do prezentacji graficznej. Z wszystkich wymienionych funkcji do konstrukcji drzew korzysta się podobnie. Wymienione funkcje mogą służyć zarówno do wyznaczania drzew regresyjnych jak i klasyfikacyjnych, ale w tym miejscu przedstawimy tylko ich klasyfikacyjną naturę. Do wizualizacji drzew klasyfikacyjnych można wykorzystać (w zależności od tego jaką funkcją wyznaczyliśmy drzewo) funkcje plot.BinaryTree(party), plot.tree(tree), text.tree(tree), draw.tree(maptree), plot.rpart(rpart) oraz text.rpart(rpart).

Aby zbudować drzewo klasyfikacyjne należy określić kryterium podziału, a więc na jaka wartość ma być minimalizowana przy tworzeniu kolejnych gałęzi (najczęściej jest to błąd klasyfikacji) oraz kryterium stopu (a wiec jak długo drzewo ma być dzielone). Różne warianty drzew umożliwiają kontrolę różnych kryteriów, w przypadku metody ctree() zarówno kryterium stopu jak i podziału można określić argumentem control (patrz opis funkcji ctree_control(party)). Poniżej przedstawiamy przykładową sesję z budową drzewa klasyfikacyjnego.

# określamy kryteria budowy drzewa klasyfikayjnego
ustawienia <- party::ctree_control(mincriterion = 0.5, testtype = "Teststatistic")
# uczymy drzewo
drzewo <- party::ctree(diabetes~glucose+insulin,
                       data=dane, subset = zbior.uczacy, controls = ustawienia)
# narysujmy je
plot(drzewo)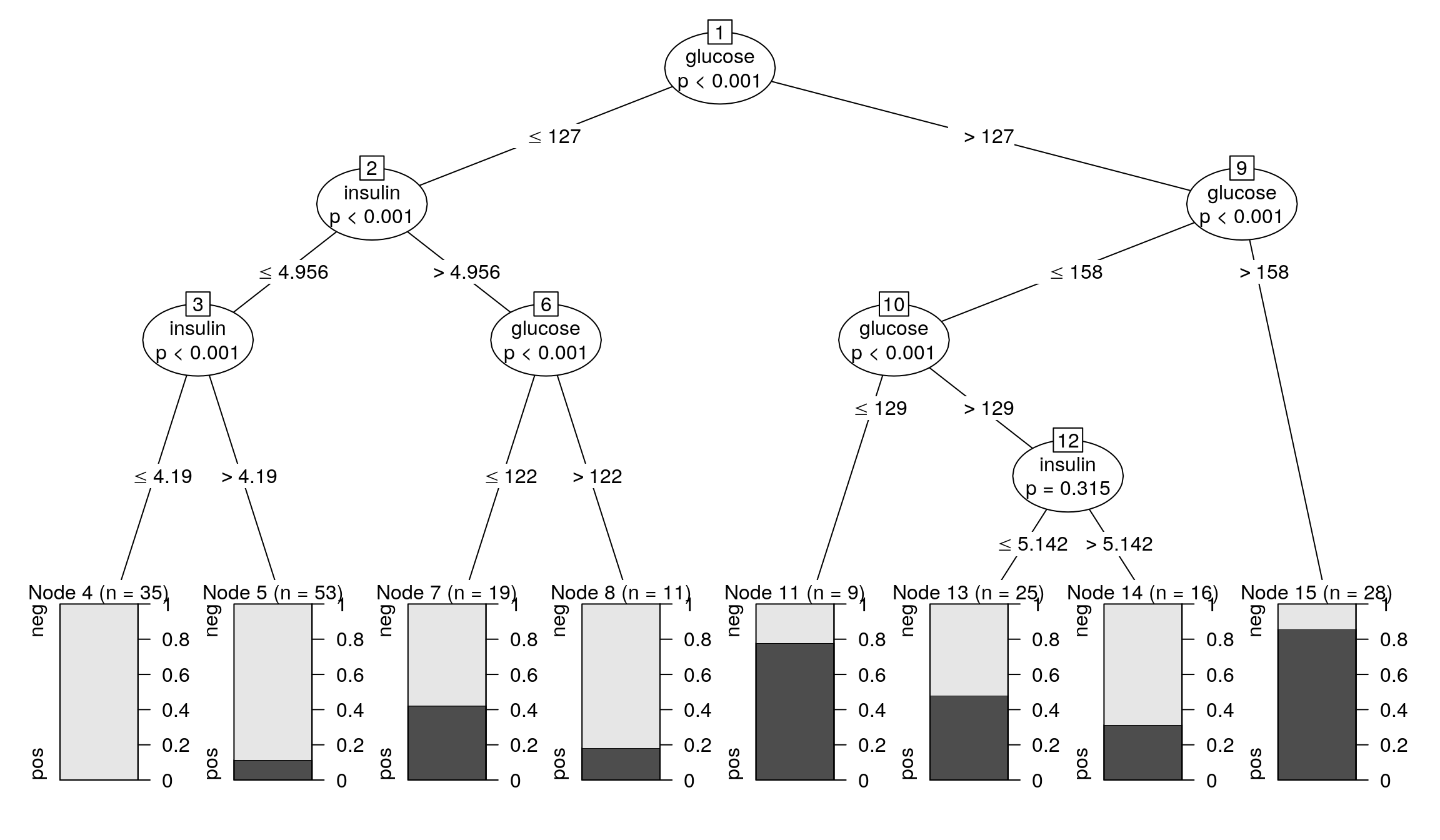

Rysunek 4.6: Przykładowe drzewo klasyfikacyjne wyznaczone funkcją ctree().

# w standardowy sposób przeprowadzamy klasyfikacje
oceny = predict(drzewo, dane[-zbior.uczacy,])
table(predykcja = oceny, prawdziwe = dane[-zbior.uczacy,3])

##          prawdziwe
## predykcja neg pos
##       neg 121  41
##       pos   9  25

drzewo <- party::ctree(dane$diabetes~dane$glucose+dane$insulin, data=dane,
                       controls = party::ctree_control(
                         mincriterion = 0.5, teststat = c("max")))
wub = predict(drzewo, siata)
plot(siata, col=kol[as.numeric(wub)], pch=15, main="ctree()",
     xlab="insulin",ylab="glucose", xlim=range(dat[,1]),ylim=range(dat[,2]))
points(dane[,1:2],pch=c(1,4)[as.numeric(dane[,3])], cex=1,
       col=kol2[as.numeric(dane[,3])], lwd=2)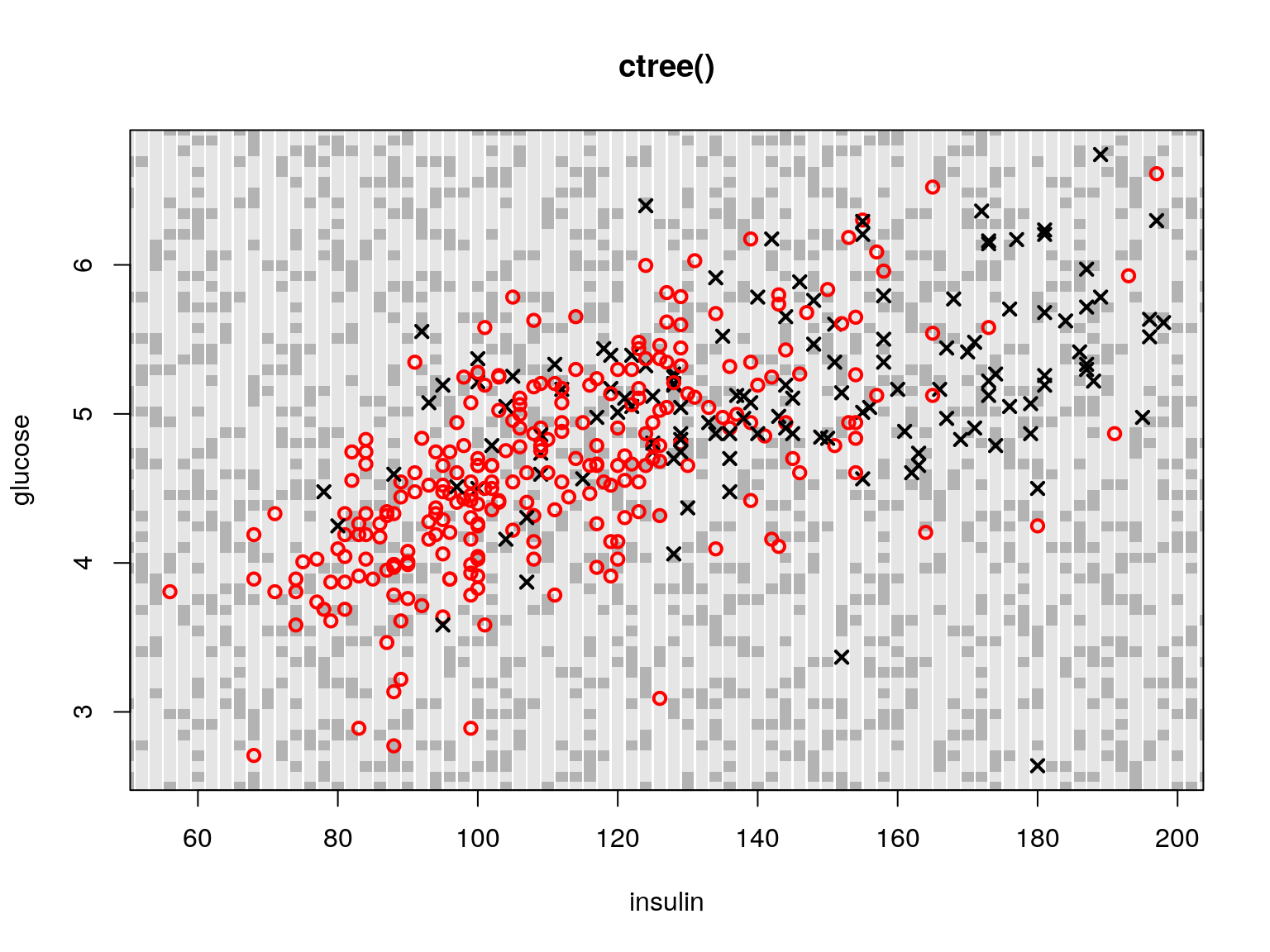

Rysunek 4.7: Przykładowe obszary decyzyjne dla drzewa klasyfikacyjnego.

Zaletą drzew jest ich łatwość w interpretacji. Narysowany klasyfikator może być oceniony i poprawiony, przez eksperta z dziedziny, której problem dotyczy.

Dla drzew zapisanych jako obiekty klasy tree lub rpart dostępne są dwie przydatne funkcje umożliwiające modyfikację drzewa. Pierwsza to prune.tree(tree) (prune.rpart(rpart)). Pozwala ona na automatyczne przycinanie drzewa, poszczególnymi argumentami tej funkcji możemy ustalić jak drzewo ma być przycięte. Można określić pożądaną liczbę węzłów w drzewie, maksymalny współczynnik błędu w liściu drzewa oraz inne kryteria. Nie zawsze przycinanie automatyczne daje satysfakcjonujące rezultaty. W sytuacji gdy drzewo potrzebuje ludzkiej ingerencji można wykorzystać funkcję snip.tree(tree) (snip.rpart(rpart)) pozwalającą użytkownikowi na wskazanie myszką które węzły drzewa maja być usunięte. Inne ciekawe funkcje to misclass.tree(tree) (wyznacza błąd klasyfikacji dla każdego węzła z drzewa) oraz partition.tree(tree) (wyznacza obszary decyzyjne dla drzew).

4.5 Lasy losowe

Wadą drzew klasyfikacyjnych jest ich mała stabilność. Są jednak sposoby by temu zaradzić. Takim sposobem jest konstruowanie komitetu klasyfikatorów a wiec użycie metody bagging lub boosting. Nie wystarczyło tu miejsca by przedstawić te metody w ich ogólnej postaci, wspomnimy o nich na przykładzie lasów losowych.

Idea, która przyświeca metodzie lasów losowych możne być streszczona w zdaniu “Niech lasy składają się z drzew”. Jak pamiętamy w metodzie bootstrap generowano replikacje danych, by ocenić zachowanie statystyki dla oryginalnego zbioru danych. Odmianą metody bootstrap w zagadnieniu klasyfikacji jest bagging. Na bazie replikacji zbioru danych konstruowane są klasyfikatory, które na drodze głosowania większością wyznaczają ostateczną klasą dla danej obserwacji. W przypadku lasów losowych komitet klasyfikatorów składa się z drzew klasyfikacyjnych, które są trenowane na replikacjach zbioru danych, dla ustalonego podzbioru zmiennych.

Ponieważ drzew w lesie jest dużo, do komitet głosujący demokratycznie charakteryzuje się większą stabilnością. Dodatkową zaletą drzew jest naturalny nieobciążony estymator błędu klasyfikacji. Generując replikacje losując metodą z powtórzeniami, średnio do replikacji nie trafia około jednej trzeciej obserwacji (w ramach ćwiczeń warto to sprawdzić). Te obserwacje, które nie trafiły do replikacji, można wykorzystać do oceny klasyfikatora nauczonego na danej replikacji. Taka ocena błędu określana jest błędem OOB (ang. out-of-bag). Jeszcze inną zaletą drzew losowych jest możliwość oceny zdolności dyskryminujących dla poszczególnych zmiennych (dzięki czemu możemy wybrać najlepszy zbiór zmiennych).

Lasy losowe dostępne są w funkcji randomForest(randomForest). Poniżej przedstawiamy przykład jej użycia. Ponieważ przy konstrukcji lasów losowych generowane są losowe replikacje zbioru danych, to aby móc odtworzyć uzyskane wyniki warto skorzystać z funkcji set.seed().

# ustawiamy ziarno generatora, by można było odtworzyć te wyniki
set.seed(1)

# ćwiczymy las
klasyfikatorRF <- randomForest::randomForest(diabetes~glucose+insulin,
                                             data=dane,
                                             subset=zbior.uczacy, importance=TRUE, proximity=TRUE)
# podsumowanie lasu
print(klasyfikatorRF)

## 
## Call:
##  randomForest(formula = diabetes ~ glucose + insulin, data = dane,      importance = TRUE, proximity = TRUE, subset = zbior.uczacy) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 1
## 
##         OOB estimate of  error rate: 28.06%
## Confusion matrix:
##     neg pos class.error
## neg 109  23   0.1742424
## pos  32  32   0.5000000

# podobnie jak dla innych klasyfikatorów funkcją predict() możemy ocenić
# etykietki na zbiorze testowym i porównać błąd klasyfikacji z błędem z
# innych metod
oceny = predict(klasyfikatorRF, dane[-zbior.uczacy,])
table(predykcja = oceny, prawdziwe = dane[-zbior.uczacy,"diabetes"])

##          prawdziwe
## predykcja neg pos
##       neg 105  37
##       pos  25  29

PimaIndiansDiabetes2 = na.omit(PimaIndiansDiabetes2)
dane = PimaIndiansDiabetes2
dane[,5] = log(dane[,5])

seqx = seq(30,210,2)
seqy = seq(2,7,0.07)
siata = as.data.frame(expand.grid(seqx, seqy))
colnames(siata) = c("glucose", "insulin")

klasyfikatorRF <- randomForest::randomForest(diabetes~glucose+insulin,
                                             data=dane,importance=TRUE, proximity=TRUE)
#klasyfikatorRF <- randomForest(diabetes~., data=dane,importance=TRUE, proximity=TRUE)
wub = predict(klasyfikatorRF, siata)
plot(siata, col=kol[as.numeric(wub)], pch=15, 
     main="randomForest()",xlim=range(dane[,"glucose"]),ylim=range(dane[,"insulin"]),
     cex=1)
points(dane[,c("glucose","insulin")],pch=c(1,4)[as.numeric(dane[,"diabetes"])], 
       cex=1, col=kol2[as.numeric(dane[,"diabetes"])], lwd=2)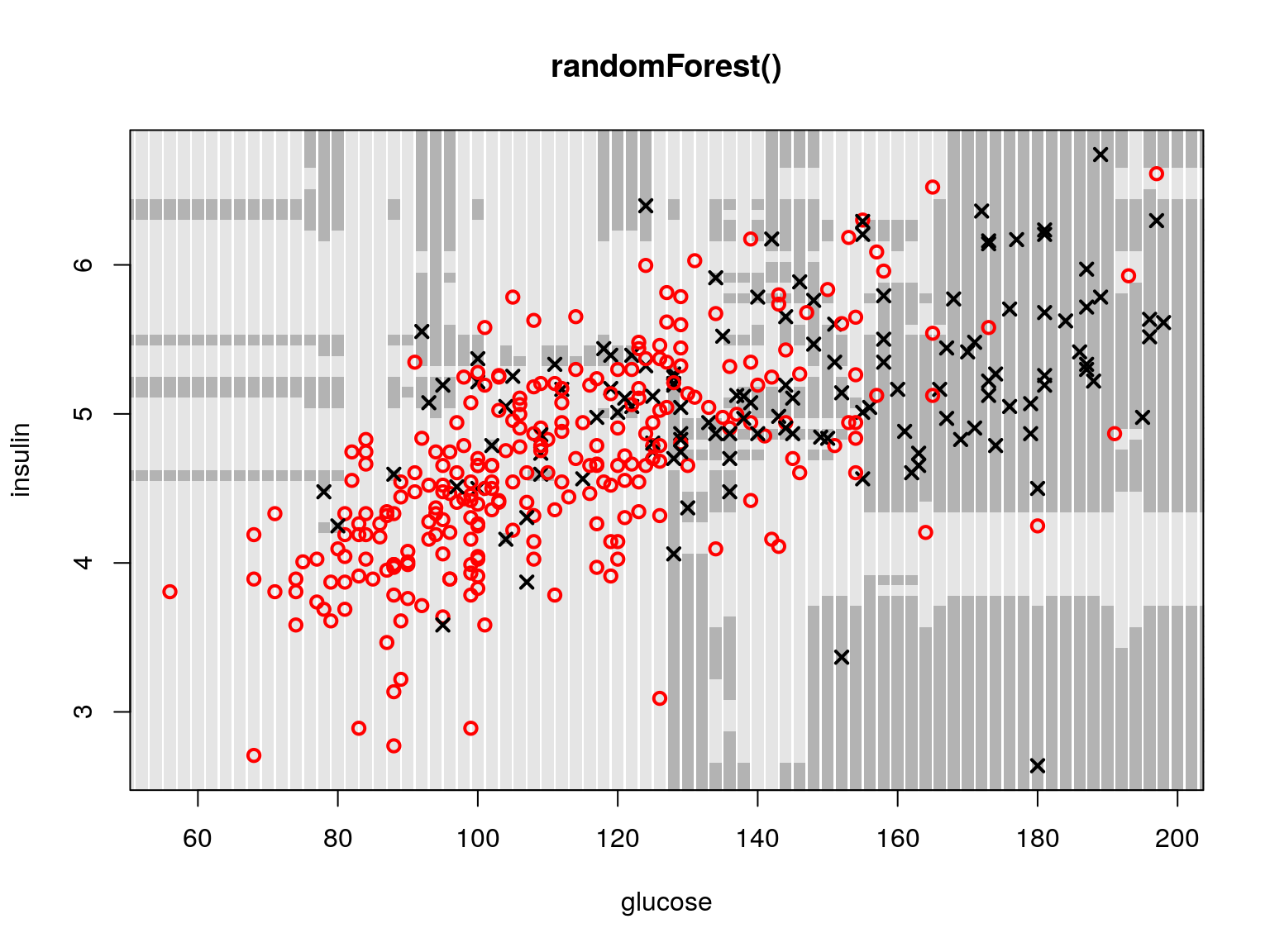

Rysunek 4.8: Przykładowe obszary decyzyjne dla lasów losowych.

Lasy losowe są uznawane za jedną z najlepszych metod klasyfikacji. Ich dodatkową zaletą jest możliwość użycia nauczonego lasu losowego do innych zagadnień niż tylko do klasyfikacji. Przykładowo na podstawie drzew z lasu można wyznaczyć ranking zmiennych, a tym samym określić które zmienne mają lepsze właściwości predykcyjne a które gorsze. Taką informację przekazuje funkcja importance(randomForest), można tę informacje również przedstawić graficznie z użyciem funkcji varImpPlot(randomForest) (przykład dla naszego zbioru danych jest przedstawiony na rysunku 4.9).

Używając lasów losowych (regresyjnych) można również wykonać imputacje, a wiec zastąpić brakujące obserwacje w zbiorze danych. Do tego celu można posłużyć się funkcją rfImpute(randomForest). Można również zdefiniować na podstawie lasów losowych miarę odstępstwa i wykrywać nią obserwacje odstające (do tego celu służy funkcja outlier(randomForest)). Można rónież używając lasów losowych przeprowadzać skalowanie wielowymiarowe, osoby zainteresowane tym tematem powinny zaznajomić się z funkcją MDSplot(randomForest)

klasyfikatorRF <- randomForest::randomForest(diabetes~ .,
                                             data=PimaIndiansDiabetes2,
                                             importance=TRUE,proximity=TRUE)
randomForest::varImpPlot(klasyfikatorRF)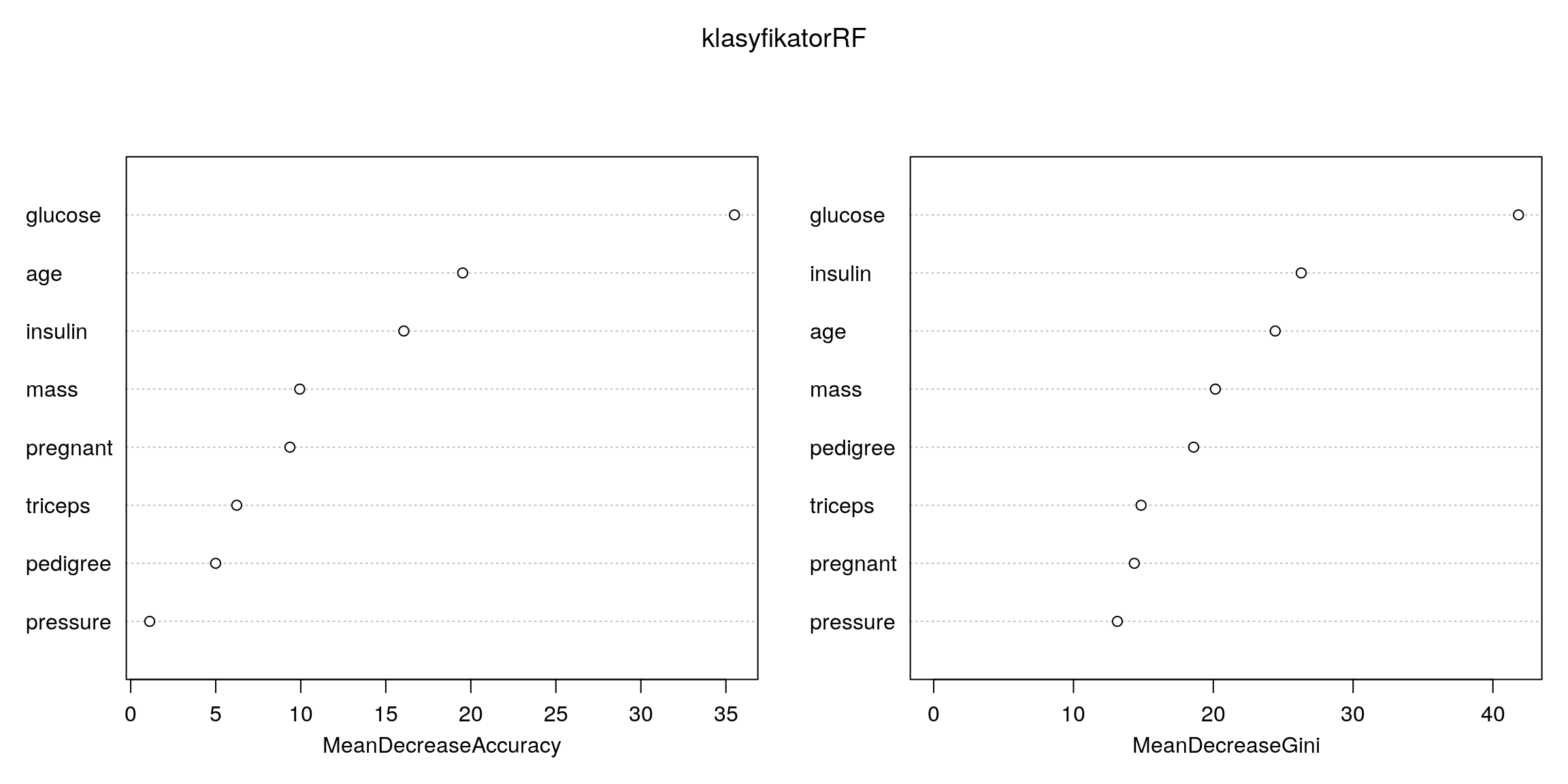

Rysunek 4.9: Ranking zmiennych wykonany przez las losowy.

4.6 Inne klasyfikatory

Powyżej wymienione metody to zaledwie początek góry lodowej funkcji do klasyfikacji dostępnych w pakiecie R. Poniżej wymienimy jeszcze kilka nazw popularnych klasyfikatorów, oraz pokażemy w których funkcjach i pakietach dane metody są dostępne.

Sieci neuronowe. Sieci neuronowe gotowe do użycia w zagadnieniach klasyfikacji są dostępne w funkcjach nnet(nnet) (prosta w użyciu sieć z jedną warstwą neuronów ukrytych) i train(AMORE) (bardziej zaawansowana funkcja do uczenia sieci neuronowych).
Metoda wektorów podpierających (SVM, ang. Support Vector Machines). Ideą wykorzystywaną w tej technice jest zwiększenie wymiaru przestrzeni obserwacji (przez dodanie nowych zmiennych np. transformacji zmiennych oryginalnych) tak by obiekty różnych klas można było rozdzielić hiperpłaszczyznami. Ta technika zyskała wielu zwolenników, funkcje pozwalające na jej wykorzystanie znajdują się w kilku pakietach np. ksvm(kernlab), svm(1071), svmlight(klaR), svmpath(svmpath).
Nearest mean classification i Nearest Shrunken Centroid Classifier. Zasady działania podobne jak dla metod analizy skupień k-średnich i PAM. Metoda Nearest mean classification dostępna w funkcji nm(klaR) wyznacza średnie dla obiektów z danej klasy i nowe obiekty klasyfikuje do poszczególnych klas na podstawie wartości odległości nowej obserwacji od wyznaczonych średnich. Metoda Nearest Shrunken Centroid Classifier dostępna w funkcji pamr.train(pamr) działa podobnie, tyle, że zamiast średnich wyznacza centroidy.
Metody bagging i boosting. Idea obu metod opiera się na tworzeniu replikacji zbioru danych, na których uczone są klasyfikatory. Wiele funkcji ze wsparciem dla tych metod znajduje się w pakiecie boost (boosting) i ipred (bagging), np. funkcje adaboost(boost), bagboost(boost), l2boost(boost), logitboost(boost), ipredbagg(ipred).