Jak regularyzować modele regresyjne?

Jak widzieliśmy w rozdziale Wybór modelu, gdy liczba zmiennych w modelu jest duża (p >> n) należy spodziewać się przeuczenia modelu.

Przeuczenie w terminologii statystycznej oznacza dużą wariancję estymatora przy małym błędzie na zbiorze uczącym.

Co zrobić by się nie przeuczać? Standardowo dla modeli regresyjnych stosuje się trzy strategie:

  1. Wybór zmiennych (subset selection), np. z użyciem kryteriów AIC/BIC/jednowymiarowe filtrowanie.
  2. Stosowanie regularyzacji opartej o karę za wielkość współczynników w modelu,
  3. Redukcja wymiaru zmiennych predykcyjnych przez zastosowanie techniki PCA/PCR.

Poniżej omówimy te strategie jedna po drugiej.

Wybór podzbioru zmiennych

Jednym ze sposobów zmniejszenia wariancji modelu regresyjnego jest budowanie go na mniejszej liczbie zmiennych.

Jak wyznaczyć tę mniejszą liczbę zmiennych?

  1. Można wybrać model o najniższej wartości kryterium AIC
  2. Można wybrać model o najniższej wartości kryterium BIC
  3. Można wybrać model tylko ze zmiennymi o zależności o istotności niższej niż $\alpha$.
load(url("https://github.com/pbiecek/StatystykaII/raw/master/MIMUW_2016/materialy/brca.rda"))
brcaSmall <- brca[,c(1, 5:10, 92:97)]

Pełny przegląd modeli. Dla każdego modelu wyznaczamy AIC i BIC.

library("e1071")
library("ggplot2")
comb <- bincombinations(ncol(brcaSmall)-1)[-1,]
crit <- matrix(0, nrow(comb), 3)

for (i in 1:nrow(comb)) {
  vnames <- colnames(brcaSmall)[which(comb[i,]==1)]
  form <- paste0("outcome~", paste0(vnames, collapse="+"))
  model <- glm(as.formula(form), data=brcaSmall, family="binomial")
  crit[i,1] <- AIC(model)
  crit[i,2] <- BIC(model)
  crit[i,3] <- sum(comb[i,]==1)
}
colnames(crit) <- c("AIC", "BIC","p")
crit <- data.frame(crit)

Porównujemy wszystkie modele z modelem wybranym przez funkcję step().

Czerwona kropka to model optymalny, zielona to model wybrany przez funkcję step().

bestStepBIC <- step(glm(outcome~., data=brcaSmall, family="binomial"), trace = 0, k = log(nrow(brcaSmall)))

ggplot(crit, aes(p,BIC)) + 
  geom_point() +
  geom_point(data=crit[which.min(crit$BIC),], color="red", size=5) +
  geom_point(data=crit[crit$BIC == BIC(bestStepBIC) &
                         crit$p == length(bestStepBIC$coefficients)-1,], color="green3", size=3) + scale_x_continuous(breaks = 1:12) + ggtitle("Najlepszy model względem BIC")

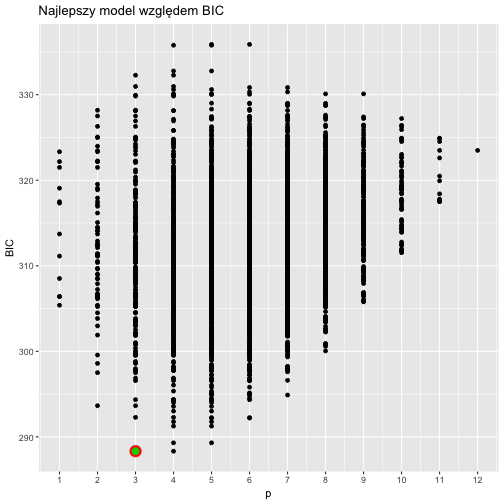
plot of chunk obic

Porównujemy wszystkie modele z modelem wybranym przez funkcję step().

Czerwona kropka to model optymalny, zielona to model wybrany przez funkcję step().

tmpFun = function(fit, aic) {
  list(size = length(fit$coefficients), aic = AIC(fit))
}

bestStepAIC <- step(glm(outcome~., data=brcaSmall, family="binomial"),keep=tmpFun,  trace = 0)

pathDF <- data.frame(size = unlist(bestStepAIC$keep[1,]),
            aic = unlist(bestStepAIC$keep[2,]))

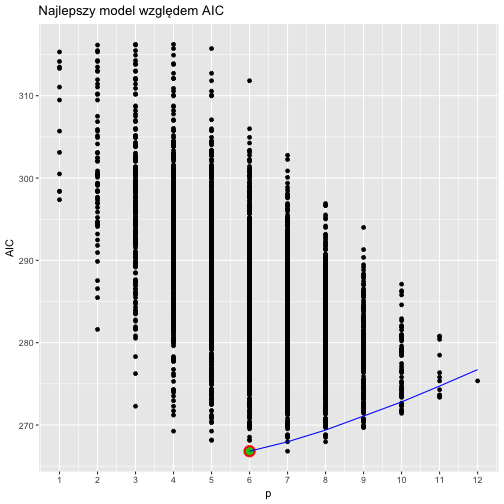
ggplot(crit, aes(p,AIC)) + 
  geom_point() +
  geom_point(data=crit[which.min(crit$AIC),], color="red", size=5) +
  geom_point(data=crit[crit$AIC == AIC(bestStepAIC) &
                         crit$p == length(bestStepAIC$coefficients)-1,], color="green3", size=3) + 
    geom_line(data=pathDF, aes(size-1, aic), color="blue") + 
  scale_x_continuous(breaks = 1:12) + ggtitle("Najlepszy model względem AIC")

plot of chunk oaic

Regularyzacja

Innym sposobem ograniczenia wariancji modelu regresyjnego jest ograniczenie wartości współczynników tego modelu.

Ograniczać można normę $L_2$ wektora współczynników (rozwiązanie znane pod nazwą regresja grzbietowa) lub normę $L_1$ wektora współczynników (rozwiązanie znane pod nazwą LASSO) lub mieszaninę tych norm (rozwiązanie znane pod nazwą sieci elastycznych).

Lasso

Dla normy $L_1$ wyznacza się estymator $\hat\beta$ ograniczony przez wartość $s$

β^lasso=argmin∣∣β∣∣1<sl(y,β0+Xβ) \hat\beta_{lasso} = {\arg\min}_{||\beta||_1 < s} l(y, \beta_0 + X \beta)

Równoważnie można ten estymator wyznaczyć przez minimalizację funkcji log wiarogodności z dodaną karą za wielkość współczynników.

β^lasso=argmin(β0,β)∈Rp+1l(y,β0+Xβ)+α∣∣β∣∣1 \hat\beta_{lasso} = {\arg \min}_{(\beta_0, \beta) \in \mathbb{R}^{p+1}} l(y, \beta_0 + X \beta) + \alpha||\beta||_1

Pomiędzy parametrami $\alpha$ i $s$ istnieje zależność 1-1.

Uwaga 1:

Współczynniki $\hat\beta_{lasso}$ mogą przyjmować wartość 0.

Regresja grzbietowa

Dla regresji grzbietowej wzór na estymator współczynników ma postać

β^ridge=argmin(β0,β)∈Rp+1l(y,β0+Xβ)+α∣∣β∣∣2 \hat\beta_{ridge} = {\arg \min}_{(\beta_0, \beta) \in \mathbb{R}^{p+1}} l(y, \beta_0 + X \beta) + \alpha||\beta||_2 W modelu gaussowskim funkcja log-wiarogodności jest proporcjonalna do RSS, mamy więc

β^ridge=argmin(β0,β)∈Rp+1(β0+Xβ−y)T(β0+Xβ−y)+λβTβ \hat\beta_{ridge} = {\arg \min}_{(\beta_0, \beta) \in \mathbb{R}^{p+1}} (\beta_0 + X \beta - y)^T(\beta_0 + X \beta - y) + \lambda \beta^T\beta

Ten estymator można wyznaczyć w sposób analityczny β^ridge=(XTX+λI)−1XTy \hat\beta_{ridge} = \left(X^TX + \lambda I\right)^{-1} X^T y

Elastic net

Dla metody elastic net, kara ma dwie składowe oparte o metrykę $L_1$ i $L_2$.

argmin(β0,β)∈Rp+1l(y,β0+Xβ)+λ[(1−α)∣∣β∣∣22/2+α∣∣β∣∣1]. {\arg \min}_{(\beta_0, \beta) \in \mathbb{R}^{p+1}} l(y, \beta_0 + X \beta) + \lambda \left[ (1-\alpha)||\beta||_2^2/2 + \alpha||\beta||_1\right].

Uwaga 1:

Aby współczynniki $\beta$ można było wspólnie ograniczać, trzeba wcześniej standaryzować macierz $X$.

Jak to zrobić w R?

library("glmnet")
X <- as.matrix(brcaSmall[,-1])
X <- scale(X)

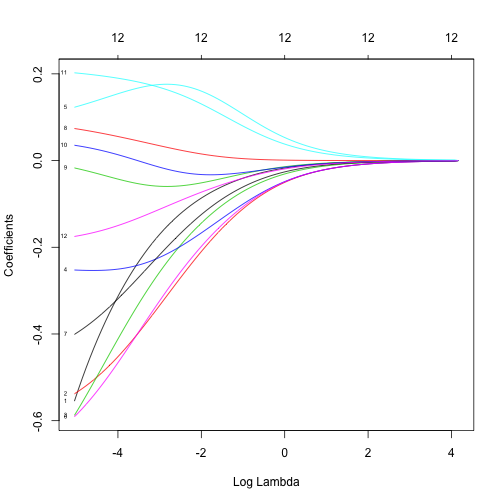
model <- glmnet(x = X, y = brcaSmall$outcome == "death in 3 years", alpha=0, family="binomial")
plot(model, xvar = "lambda", label = TRUE)

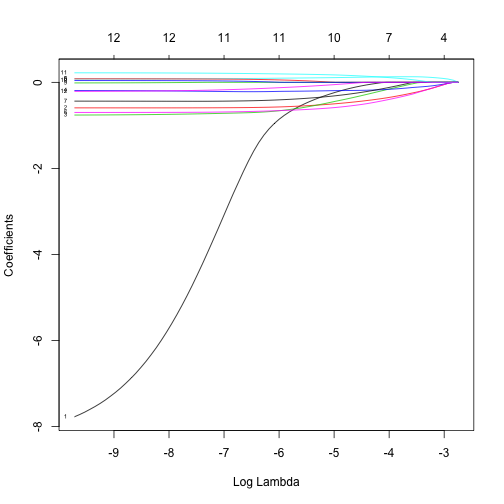
plot of chunk glmnet

model <- glmnet(x = X, y = brcaSmall$outcome == "death in 3 years", alpha=1, family="binomial")
plot(model, xvar = "lambda", label = TRUE)

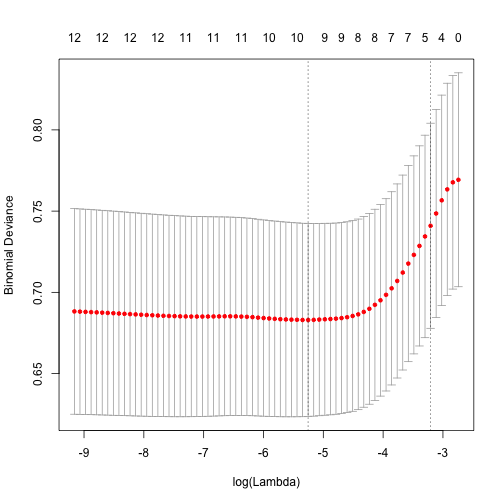
plot of chunk glmnet

cvfit = cv.glmnet(x = X, y = brcaSmall$outcome == "death in 3 years", alpha=1, family="binomial")
plot(cvfit)

plot of chunk glmnet

coef(cvfit, s = "lambda.min")

## 13 x 1 sparse Matrix of class "dgCMatrix"
##                       1
## (Intercept) -2.35487481
## ADAM29      -0.34967342
## ALKBH1      -0.52442702
## CLIC6       -0.51475641
## CTSO        -0.19908113
## EIF2B3       0.10576319
## ENTPD1      -0.61199370
## ICAM3       -0.34654417
## LRP2         0.01954816
## FCGR1B       .         
## ABI3BP       .         
## LOC284837    0.18055607
## EMR3        -0.07480810

Więcej instrukcji na stronie https://web.stanford.edu/~hastie/glmnet/glmnet_alpha.html

PCR - Principal component regression

Metoda PCR to złożenie regresji i metody PCA.

W pierwszym kroku redukuje się wymiar - liczbę zmiennych przez wykonanie PCA (Principal component analysis).

Następnie buduje się model regresyjny na nowych zmiennych.

W programie R można tę regresję przeprowadzić funkcją pcr{pls}.